Раздел 5. Приложение

Раздел 5. Приложение

§1. Вариационное исчисление. Простейшая (основная) задача

Вариационным исчислением называется раздел математики, в котором исследуются экстремальные задачи в бесконечномерных функциональных пространствах. Применяя терминологию теории оптимизации, можно сказать, что предметом изучения этой науки являются экстремальные задачи, в которых роль целевой функции играет функционал, а роль множества допустимых решений – множество функций. Напомним в связи с этим, что функционалом называется любое отображение некоторого множества функций в пространство действительных чисел.

Специфическим методом вариационного исчисления, породившим его название, является анализ вариаций (допустимых кривых, функционала), применяемый при доказательстве оптимальности допустимых функций в смысле минимизации функционала качества.

В простейшей (основной) задаче вариационного исчисления среди всех плоских кривых, являющихся графиками функций вида и проходящих через две заданные точки и , , требуется выделить такую кривую, на которой достигает своего минимума интегральный целевой функционал:

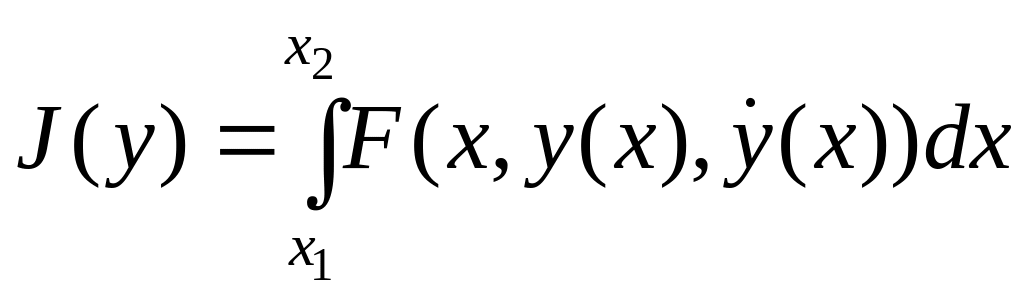, (5.1)

где F – фиксированная скалярная функция трех переменных, называемая интегрантом, . Множество функций, на котором минимизируется целевой функционал, имеет вид:

(см. рис. 5.1).

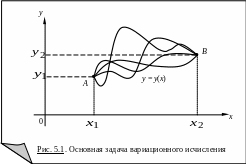
Функции , непрерывные на отрезке вместе со своими производными , назовем допустимыми кривыми. Будем предполагать, что Y содержит, по крайней мере, одну подобную функцию.

Запишем простейшую задачу вариационного исчисления в следующем виде:

,

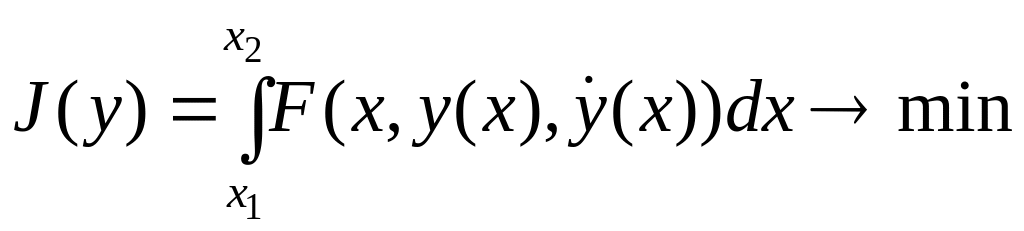, , (5.2)

, .

( – пространство k раз непрерывно дифференцируемых функций на отрезке ).

Если, например, в качестве F взять функцию вида , то интеграл (5.1) определяет длину кривой и простейшая вариационная задача заключается в определении плоской линии кратчайшей длины, соединяющей точки A и B.

Пример 5.1 (задача о брахистохроне). Пусть в вертикальной плоскости имеются две точки A и B, причем первая выше второй. Данные точки могут быть соединены различными плоскими кривыми (в частности, и прямой линией). Предположим, что в A помещена материальная точка массы m, которая под действием силы тяжести может "скатываться" из точки A в точку B по различным кривым, соединяющим A и B. Задача заключается в отыскании такой кривой (если она существует), по которой материальная точка достигнет B за кратчайшее время. Такую кривую называют брахистохроной.

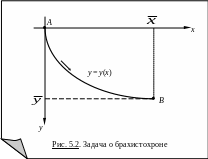Для того чтобы дать математическую формулировку задачи, введем на рассматриваемой плоскости прямоугольную систему координат. Поместим ее начало в точку A и направим ось ординат вертикально вниз (рис. 5.2). Обозначим координаты точки B через . По условию, материальная точка начинает двигаться из без начальной скорости, поэтому, согласно закону сохранения энергии:

,

где v – скорость, y – ордината материальной точки, g – ускорение свободного падения. Отсюда находим . Будем считать, что – уравнение кривой, по которой "скатывается" материальная точка. Если обозначить через s длину пройденного точкой пути, а через t – время, то можно записать:

.

Следовательно,

.

Интегрируя, получаем следующее выражение:

, (5.3)

где T – время, в течение которого материальная точка движется вдоль кривой ( ) из A в B.

Равенство (5.3) задает функционал T, определенный на множестве кривых (т.е. функций) вида , подчиненных граничным условиям:

, . (5.4)

Из физических соображений ясно, что рассматриваемые кривые не должны иметь "изломов" и поэтому функции должны быть гладкими (непрерывно дифференцируемыми) на отрезке , т.е. .

Формальная постановка задачи о брахистохроне такова: среди всех функций вида , непрерывно дифференцируемых на и удовлетворяющих условиям (5.4), требуется найти такую функцию, которая (если она существует) реализует минимум функционала:

.

Задача о брахистохроне принадлежит к классу простейших задач вариационного исчисления.

Простейшая вариационная задача заключается в отыскании глобального минимума целевого функционала на множестве Y. Однако в ней можно рассматривать также и локальные минимумы.

Напомним, что точка называется точкой локального минимума функции , если для всех и точкой глобального минимума на множестве X, если для всех . Здесь – -окрестность точки , .

Зададим в пространстве норму:

.

Тогда можно определить -окрестность функции :

.

Такую окрестность называют -окрестностью первого порядка. При малом она состоит из функций y(x), значения которых (а также значения их первых производных) мало отличаются от значений (соответственно от ) в одних и тех же точках .

В соответствии с этим реализует слабый локальный минимум (является слабой минималью) функционала J на множестве , если можно указать такое число , что неравенство имеет место для всех (см. рис. 5.3).

Аналогичным образом рассмотрим норму пространства непрерывных функций :

.

Так как , то эту норму можно использовать как еще одну норму в пространстве . В соответствии с этим вводится понятие -окрестности нулевого порядка

,

которую при малом составляют функции y, чьи значения мало отличаются от ; при этом производные могут отличаться значительно.

Говорят, что реализует сильный локальный минимум (является сильной минималью) функционала J на множестве , если существует такое, что неравенство выполнено для всех (см. рис. 5.4).

Очевидно, что сильная минималь является и слабой, тогда все необходимые условия слабого минимума будут и необходимыми условиями сильного минимума. Поэтому в дальнейшем будут исследоваться только слабые минимали.

Основным методом исследования экстремальных задач в функциональных пространствах является метод вариаций, обобщающий метод исследования функций на максимум и минимум с помощью дифференциалов.

Пусть – некоторая допустимая кривая простейшей задачи вариационного исчисления.

Определение 5.1. Вариацией функции называется разность , где – произвольная функция из Y, .

Для данной допустимой кривой простейшей задачи вариационного исчисления функцию будем называть допустимой вариацией, если – допустимая кривая задачи (5.2).

Заметим, что вариация – это не то же самое, что приращение функции в точке. Приращение функции в точке есть число, равное разности двух значений функции, а вариация – это функция, равная разности двух функций, рассматриваемых в качестве аргумента функционала.

Из определения допустимой кривой следует, что функция , , является вариацией допустимой кривой в том и только в том случае, когда

, . (5.5)

Рассмотрим функционал J, определенный на допустимых кривых. Пусть его приращение на кривой , соответствующее вариации , можно представить в следующем виде:

,

где – функционал, линейный относительно , а – функционал, являющийся бесконечно малой более высокого порядка, чем при . Тогда функционал J называется дифференцируемым в точке y, а линейный функционал – сильным дифференциалом.

Определение 5.2. Первой вариацией функционала J называется величина

.

Если функционал линеен по , то он называется слабым дифференциалом в точке y.

Теорема 5.1. Если функционал J дифференцируем в точке y, то его слабый дифференциал в точке y существует и совпадает с сильным дифференциалом.

Доказательство этой теоремы можно найти, например, в [8].

Для функционала (5.1) простейшей задачи вариационного исчисления получаем:

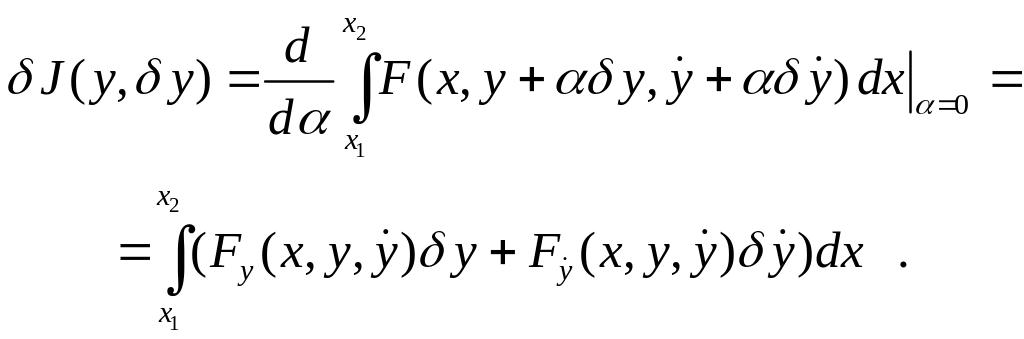
Для законности такого дифференцирования достаточно предположить, что функция F, а также ее частные производные и непрерывны. Оказывается, что эти условия являются необходимыми признаками для слабого локального минимума.

Теорема 5.2. Пусть функция реализует слабый локальный минимум в простейшей вариационной задаче. Если при этом функции F, и непрерывны по всем своим аргументам, то первая вариация целевого функционала (относительно элемента y) тождественно равна нулю:

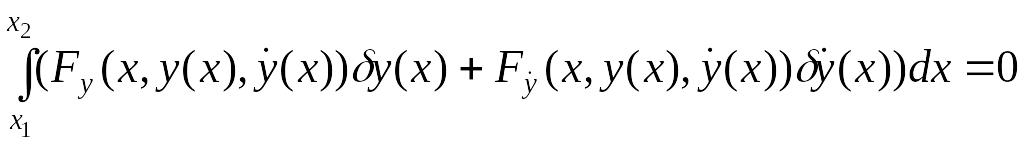(5.6)

для всех функций , удовлетворяющих условиям (5.5).

Дальнейшее исследование условий слабого минимума в вариационных задачах опирается на две леммы, называемые соответственно первая и вторая основные леммы вариационного исчисления.

Лемма 5.1 (Лагранжа). Пусть  – непрерывная на отрезке функция одной переменной x. Если равенство

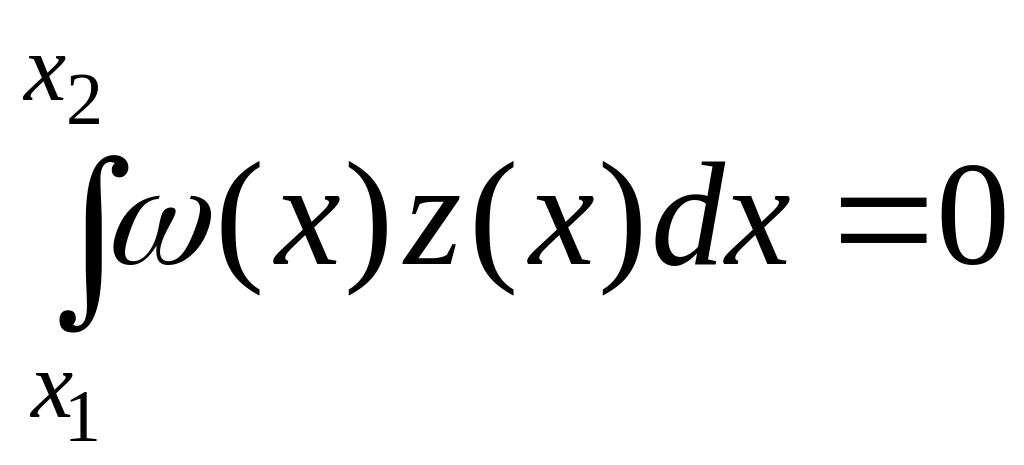
имеет место для любой функции , обладающей свойством (5.5), то для всех .

Лемма 5.2 (Дюбуа-Реймона). Пусть – непрерывная на функция и равенство

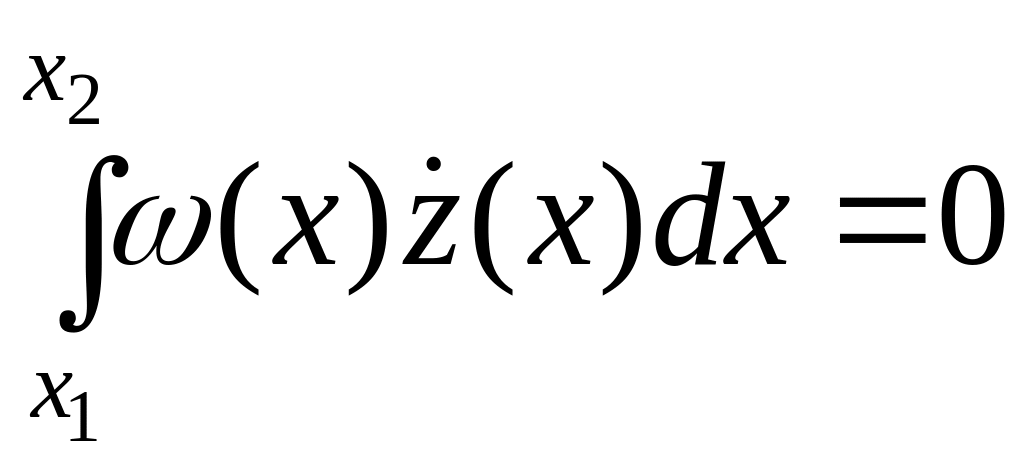
выполняется для всех z, удовлетворяющих условиям (5.5). Тогда функция постоянна, т.е. для некоторого числа C равенство верно при всех .

Как видно из условий, данные леммы обеспечивают достаточные условия интегрального типа, при выполнении которых заданная функция обращается в нуль (лемма Лагранжа) или постоянна (лемма Дюбуа-Реймона).

Вернемся теперь к необходимому условию (5.6) и преобразуем его к более удобному виду. Интегрируя по частям первое из слагаемых (5.6) и используя равенства из (5.5), получаем:

.

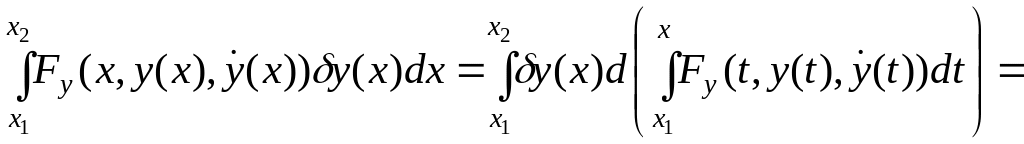
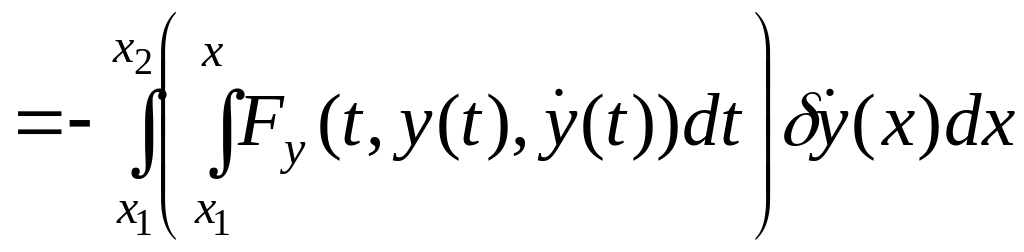Тогда равенство (5.6) можно записать в виде:

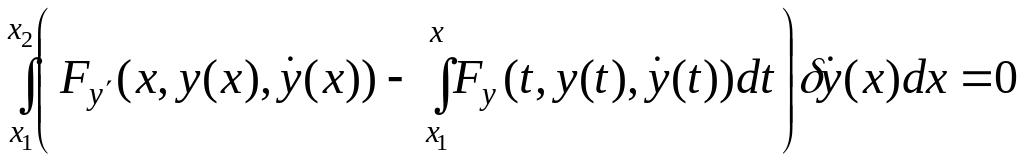
для всех , удовлетворяющих условиям (5.5).

Теперь воспользуемся леммой 5.2:

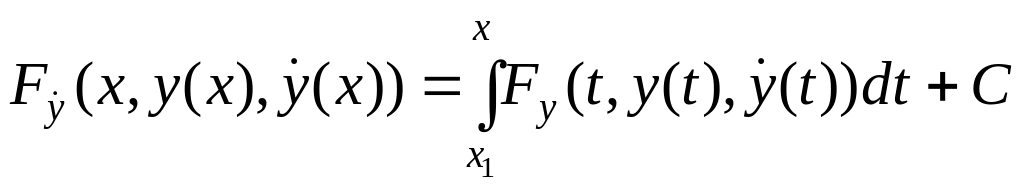, , (5.7)

где C – некоторая постоянная. Правая часть полученного равенства является непрерывно дифференцируемой по x функцией. Значит, левая часть равенства – также непрерывно дифференцируемая по x функция. Дифференцируя обе части равенства (5.7), имеем:

, .

Полученный результат можно сформулировать в виде следующей теоремы.

Теорема 5.3. Пусть функция F непрерывна по всем своим аргументам вместе с частными производными и . Если функция – слабая минималь в задаче (5.2), то она является решением дифференциального уравнения

, (5.8)

называемого уравнением Эйлера.

Замечание. Теорема 5.3 остается справедливой и для задачи максимизации функционала (5.1), поскольку уравнение (5.8) при замене функции F на (т.е. функционала J на функционал ) не меняется.

Решение уравнения Эйлера (5.8) называют экстремалью функционала J.

Как следует из теоремы 5.3, для определения экстремали нужно решать краевую задачу второго порядка:

, , . (5.9)

Для этого находят общее решение уравнения Эйлера, которое зависит от двух произвольных постоянных, а затем определяют значения этих постоянных с помощью краевых условий. Если простейшая вариационная задача имеет решение, то оно находится среди экстремалей. При этом экстремаль не обязательно является слабой минималью рассматриваемой задачи.

Пример 5.2. Рассмотрим задачу минимизации функционала вида

на множестве функций из пространства , удовлетворяющих граничным условиям . Это простейшая задача вариационного исчисления, для которой уравнение Эйлера имеет вид

.

Общее решение такого дифференциального уравнения определяется формулой

.

Единственная функция этого семейства, удовлетворяющая заданным граничным условиям, есть

, .

Таким образом, в данной задаче имеется только одна экстремаль. Однако найденная экстремаль не реализует даже слабого локального минимума функционала J. Действительно, рассмотрим последовательность допустимых функций

, .

Для этой последовательности

,

а значит, , т.е. согласно определению предела последовательности, в любой окрестности элемента найдутся элементы последовательности . Вычисляя значение функционала на членах этой последовательности

,

убеждаемся в том, что не может доставлять слабый локальный минимум.

Пример 5.3. Найдем экстремали функционала

,

удовлетворяющие краевым условиям , .

Интегрант данного функционала является непрерывно дифференцируемой функцией своих аргументов. Поэтому можно применить теорему 5.3. Поскольку , , то уравнение Эйлера для функционала J имеет вид или

.

Это – дифференциальное уравнение второго порядка, которое распадается на два уравнения: и . Общее решение первого имеет вид , а общее решение второго – . При этом все функции второго семейства входят в первое семейство. Поэтому все экстремали рассматриваемого функционала имеют вид .

Постоянные интегрирования и находим из краевых условий. Полагая и , приходим к системе линейных алгебраических уравнений относительно , :

Из этой системы находим , . Итак, поставленным краевым условиям удовлетворяет лишь одна экстремаль рассматриваемого функционала: .

Рассмотрим некоторые частные случаи уравнения Эйлера.

1. Функция F не зависит от . В этом случае и уравнение Эйлера имеет вид:

,

т.е. является алгебраическим уравнением относительно неизвестной функции . Решения этого уравнения (экстремали функционала) могут и не удовлетворять поставленным краевым условиям, тогда задача (5.2) решения не имеет.

2. Функция F линейно зависит от . Этот случай, включающий в себя и предыдущий, охватывает те функционалы, интегранты которых удовлетворяют условию . Такие функционалы называют вырожденными. Если

,

то уравнение Эйлера принимает вид:

.

Раскрывая производную по правилу дифференцирования сложной функции, получаем или

. (5.10)

Это уравнение, как и в предыдущем случае, алгебраическое. Его решения могут не удовлетворять краевым условиям. При этом, если выражение представляет собой полный дифференциал, то уравнение (5.10) является тождеством относительно x и y. Тогда любая функция является экстремалью функционала J.

3. Функция F зависит только от . В этом случае интегрант имеет вид , а уравнение Эйлера –

.

Данное уравнение допускает понижение порядка: . В результате получается алгебраическое уравнение относительно , все решения которого можно записать в виде , где – некоторая константа. Тогда экстремалями функционала с интегрантом рассматриваемого типа является семейство линейных функций с произвольными постоянными и .

4. Функция F не зависит от y. Этот случай включает в себя предыдущий. Интегрант имеет вид , а уравнение Эйлера сводится к виду:

.

Как и выше, оно допускает понижение порядка: . А это есть либо обыкновенное дифференциальное уравнение первого порядка, либо алгебраическое уравнение (например, как в предыдущем случае).

5. Функция F не зависит явно от x. В этом случае интегрант имеет вид . При дополнительном предположении, что , уравнение Эйлера по правилу дифференцирования сложной функции сводится к следующему виду:

.

Умножив его на , получим:

.

Таким образом, и в этом случае уравнение Эйлера допускает понижение порядка: .

Уравнение Эйлера зачастую способно дать исчерпывающий ответ на поставленную задачу о минимуме функционала. Если из содержательного смысла задачи вытекает, что она имеет решение, а функционал имеет лишь одну экстремаль, удовлетворяющую краевым условиям, то эта экстремаль и будет решением задачи (5.2) (т.е. слабой минималью). Однако в большинстве случаев уравнение Эйлера, как необходимое условие, дает множество экстремалей, среди которых и следует искать слабые минимали.

Чтобы среди экстремалей найти решение вариационной задачи, нужно использовать достаточные условия экстремума. Для их формулировки вводится понятие второй вариации, и достаточные условия строятся на поведении этой вариации вблизи исследуемой экстремали.

Определение 5.3. Функционал J называется дважды дифференцируемым в точке y, если его приращение можно представить в виде

,

где – квадратичный функционал по переменной , называемый второй вариацией функционала J в точке y, а – функционал, являющийся бесконечно малой более высокого порядка, чем при .

Для простейшей задачи вариационного исчисления вторая вариация функционала (5.1) вычисляется по формуле:

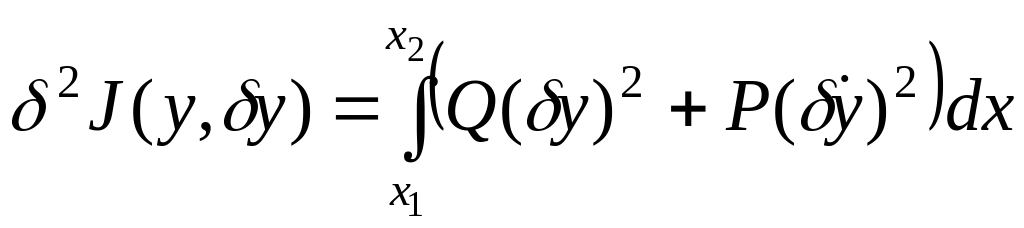, (5.11)

где

, .

Запишем для функционала (5.11) уравнение Эйлера (называемое в этом случае также уравнением Якоби) исходного функционала J. Вместе с краевыми условиями получим краевую задачу для обыкновенного дифференциального уравнения:

, . (5.12)

Эта задача имеет одно тривиальное решение ( ), но могут существовать и ненулевые решения.

Рассмотрим ненулевое решение краевой задачи (5.12). Если точка такова, что , в то время как при , то точку называют сопряженной точке . Отсутствие на полуинтервале точек, сопряженных точке , означает, что задача (5.12) не имеет ненулевых решений.

Относительно достаточного условия слабого минимума имеет место следующее утверждение.

Теорема 5.4. Допустимая кривая является слабой минималью простейшей задачи (5.2), если одновременно выполняются условия:

а) функция y является экстремалью функционала J;

б) для функции y выполняется усиленное условие Лежандра:

, ;

в) на интервале нет точек, сопряженных точке (усиленное условие Якоби).

Вернемся к примеру 5.2. Мы получили, что в нем существует единственная экстремаль , , которая не является решением задачи. Покажем, что условия теоремы 5.4 при этом нарушаются.

Так как , то условие Лежандра вдоль экстремали выполнено.

Уравнение Якоби вдоль экстремали имеет вид: . Как следует из проведенных ранее вычислений, каждое его нетривиальное решение, удовлетворяющее условию , имеет вид . Второе краевое условие , где , приводит к уравнению , или, так как должно быть нетривиальным, . Так как , то , т.е. на отрезке есть точка , сопряженная с . Значит, рассматриваемая экстремаль не удовлетворяет условию Якоби и не может быть решением задачи. Поскольку других экстремалей в этой задаче нет, то решения в ней не существует.

Теперь можно привести алгоритм решения простейших вариационных задач вида (5.2).

Этап 1. Записать уравнение Эйлера (5.8).

Этап 2. Найти общее решение уравнения Эйлера с точностью до постоянных интегрирования.

Этап 3. Решить краевую задачу (5.9).

Этап 4. Для всех найденных экстремалей проверить достаточные условия (теорема 5.4) и выбрать слабые минимали задачи (5.2).

Простейшая (или основная) задача вариационного исчисления допускает разнообразные обобщения. Приведем краткое описание наиболее типичных из них.

Задача с нефиксированным отрезком отличается от основной тем, что, по крайней мере, одно из чисел , не задается, а выбирается из условия минимума функционала (5.1).

Задача с подвижными концами характеризуется тем, что в ней вместо условий , требуется, чтобы левый конец кривой лежал на заданной линии , а правый – на линии (см. рис. 5.5).

Обширный класс связанных задач вариационного исчисления получается из основной задачи добавлением дополнительных ограничений (связей) на допустимую кривую. Если эти связи имеют вид:

, ,

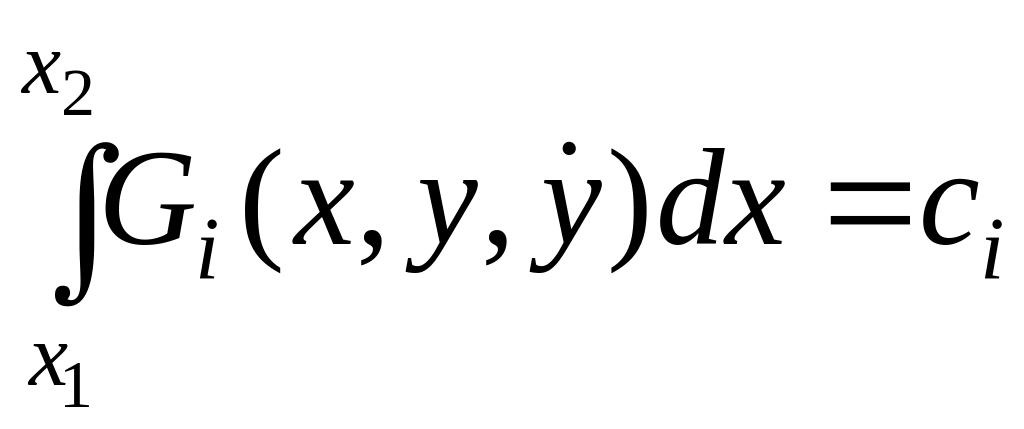то задача называется изопериметрической.

Часто связи задаются с помощью дифференциальных уравнений

, ,

и называются дифференциальными.

Вариационные задачи с высшими производными отличаются от основной задачи тем, что в них при соответствующих краевых условиях минимизируется функционал

,

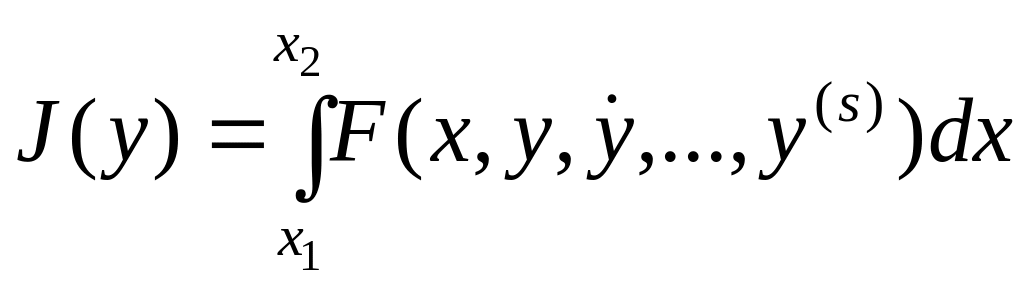заданный с помощью высших производных функции .

Многомерные вариационные задачи – это задачи, в которых минимизация производится среди функций многих переменных.

Результаты и методы, описанные для основной задачи, могут быть обобщены и на случай решения этих задач. Для более углубленного изучения этих вопросов интересующимся читателям можно рекомендовать, например, [8, 13, 23, 38], а также другие книги по соответствующей тематике.