§3. Уравнение Беллмана как необходимое условие оптимальности программного управления

Оригинальный подход к решению задачи оптимального управления (как дискретной, так и непрерывной), предложенный группой американских математиков во главе с Р. Беллманом, получил название динамического программирования [4].

В общем случае динамическим программированием называется метод решения оптимизационных задач (статических или динамических), основанный на разбиении исходной задачи на последовательность рекуррентных и более простых подзадач. Этот метод находит применение как в дискретных, так и в непрерывных задачах оптимального управления.

Метод динамического программирования мы будем рассматривать применительно к задаче (4.1)-(4.4). Он базируется на уравнении Беллмана, которое получается на основе сформулированного выше принципа оптимальности.

Введем множество

Предположение А. Пусть в каждый момент t[t₀,T] и для каждой точки xM(t) в задаче (x, T – t) существует оптимальное программное управление.

Благодаря этому предположению каждой парe (t, x)Г можно ставить в соответствие число

, (4.5)

где – сужение множества U на [t,T].

Определение 4.2. Функция , определенная формулой (4.5), называется функцией Беллмана.

Из (4.5) следует:

V(T, x) = F(x) для любого xM(T), (4.6)

.

Предположим, что принцип оптимальности Беллмана выполнен, тогда для каждой позиции (t, x)Г мы можем написать

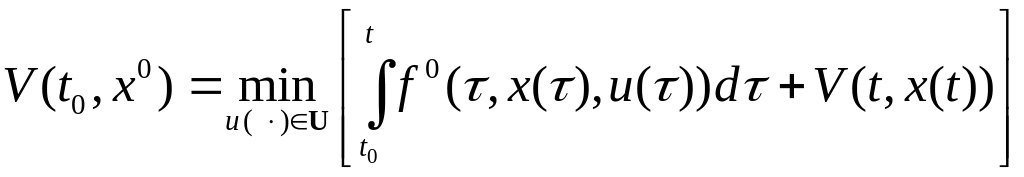. (4.7)

Предположение В. Функция V непрерывна на множестве Г и имеет в любой его внутренней точке непрерывные частные производные , , i = 1, ..., n.

Наша задача – построить уравнение, решением которого была бы функция Беллмана (4.5).

Для вывода уравнения Беллмана рассмотрим текущую задачу (x, T – t), (t, x) int Г. Придадим моменту t приращение t и построим следующее допустимое в этой задаче управление :

где uU – постоянный вектор, – оптимальное программное управление на отрезке [t + t, T]. Соответствующую этому управлению траекторию обозначим . Число t настолько мало, что (такое число существует, так как (t, x) int Г), причем , t    T.

С помощью управления на промежутке [t, t + t] система переводится из точки x в точку под действием постоянного управления u, а затем при  > t + t применяется оптимальное программное управление (которое существует согласно предположению А).

Значение функционала (4.4), соответствующее управлению на отрезке [t,T], есть:

.

По определению функции Беллмана , а последние два слагаемых есть . Поэтому мы можем написать

Поделим обе части на t > 0:

При t  0 по "первой интегральной теореме о среднем" второе слагаемое равно . Поэтому, переходя к пределу и используя предположение B, имеем

Применяя правило дифференцирования сложной функции, имеем:

Подставляя выражение для из (4.1), имеем:

(4.8)

Таким образом, мы доказали следующее утверждение.

Лемма 4.1. Пусть в задаче (4.1)-(4.4) выполнены принцип оптимальности Беллмана и предположения А и В. Тогда в любой позиции (t, x)Г и для любого вектора u = u(t)U функция Беллмана V(t, x) удовлетворяет неравенству (4.8).

Для оптимального программного управления в задаче (x, T – t), согласно принципа оптимальности, имеем (см (4.7)):

Действуя как и выше, отсюда получаем

(4.9)

или, учитывая, что и в фиксированный момент t , имеем:

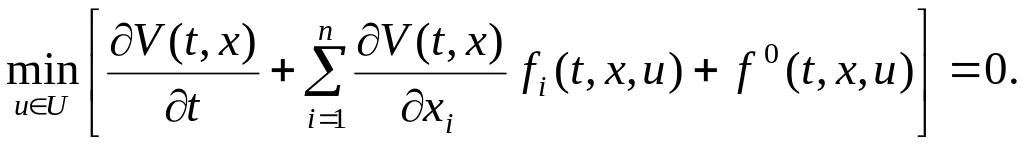(4.10)

Равенство (4.10) называется уравнением Беллмана (относительно функции Беллмана V(t, x)).

Таким образом, доказано следующее утверждение.

Теорема 4.1. Пусть в задаче (4.1)-(4.4) выполнены предположения А и В. Тогда в любой позиции (t, x)Г и для оптимального программного управления в текущей задаче (x, T – t) функция Беллмана V(t, x) удовлетворяет уравнению (4.9) (или, что то же самое, уравнению (4.10)).

По построению, равенство (4.10) является необходимым условием оптимальности и его можно использовать для вычисления оптимального программного управления в задаче (4.1)-(4.4).

В векторной форме уравнение Беллмана имеет вид:

Хотя производные функции V в это уравнение входят линейно, из-за наличия операции минимизации, уравнение (4.10) линейным не является.

Как частный случай приведем уравнение Беллмана для задачи на быстродействие.

Предположим, что задача (4.1)-(4.4) автономна, время Т не фиксировано, t₀ = 0, M(T) = x¹, f ⁰(t, x, u)  1, F(x)  0. Тогда мы имеем задачу быстрейшего перевода системы из заданной точки x⁰ в заданную точку x¹ – задачу на быстродействие с закрепленными концами и свободным временем T .

Для этой задачи функция Беллмана V имеет смысл минимального времени перехода системы (4.1) из состояния x в фиксированное состояние x¹ и не зависит от t, т.е. V = V(x). Если допустить, что выполнены оба предположения A и B, то уравнение Беллмана (4.10) принимает вид

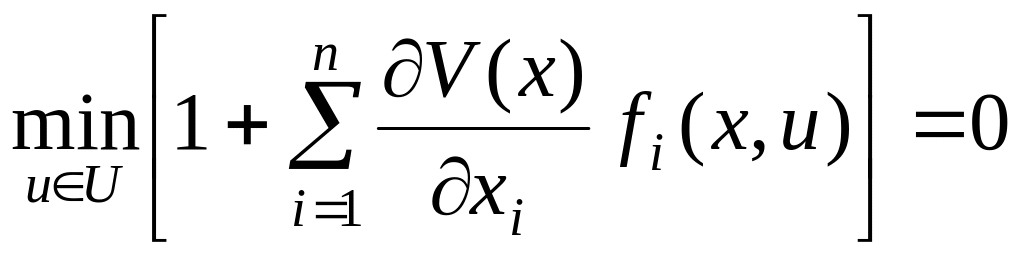
или

(4.11)

Граничное условие для (4.11) имеет вид (см. (4.6)):

V(x¹) = 0.

Очевидно, что если – оптимальный процесс в рассматриваемой задаче, то на отрезке [t₀,T] выполняется тождество

.

Уравнение Беллмана (4.11) имеет наглядную геометрическую интерпретацию. Пусть объект находится в некотором состоянии . Поверхность (линия уровня функции Беллмана, проходящая через эту точку ) представляет собой множество всех точек фазового пространства, из которых система переходит в точку x¹ за одно и то же время . Из соотношения (4.11) следует, что

.

Так как максимум в левой части равенства достигается при значении оптимального управления, соответствующего состоянию , то "оптимальный вектор фазовой скорости" образует острый угол с вектором антиградиента (т.е. направлен в сторону убывания функции V). Поэтому фазовая точка на оптимальной траектории перемещается в сторону линии уровня функции V с наименьшим временем перехода .

Как будет показано в следующем параграфе, с помощью уравнения Беллмана в некоторых случаях удается построить оптимальное синтезирующее управление в задаче (4.1)-(4.4).