Раздел 4. Синтез оптимальных управлений

Раздел 4. Синтез оптимальных управлений

§1. Задача синтеза и ее обсуждение

Рассмотрим следующую задачу оптимального управления с фиксированным временем окончания T > t₀ и свободным правым концом:

(4.1)

x(t)M(t) (M(t₀) = x⁰), t₀  t  T; (4.2)

u(t)U  R^m, t₀  t  T; (4.3)

(4.4)

Задачу (4.1)-(4.4) обозначим символом (x⁰, T – t₀), подчеркивая, что она начинается из состояния x⁰ и имеет продолжительность T – t₀.

Обозначим M = {M(t),  t₀  t  T}.

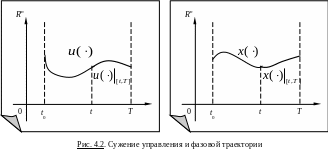
Условие (4.2) называется фазовым ограничением, оно говорит о том, что в течение отрезка [t₀,T] траектория системы (4.1) не должна выходить за пределы многообразия M (рис. 4.1).

Функции f, f ⁰, F предполагаются непрерывными по совокупности своих переменных; F определена на терминальном множестве M(T); U – компакт.

Данную задачу будем рассматривать в классе U кусочно-непрерывных управлений, удовлетворяющих условию (4.3).

Будем предполагать, что для каждого допустимого управления однозначно определено кусочно-гладкое решение системы (4.1) из начального состояния x⁰.

Задача управления состоит в выборе такого управления , для которого соответствующая траектория в момент T приходит в терминальное множество M(T), целиком оставаясь на отрезке [t₀,T] во множестве M.

Задача оптимального управления состоит в совершении такого перехода по такой траектории , чтобы вдоль нее значение функционала (4.4) было минимальным.

Если найдено соответствующее этой траектории управление , то задача (4.1)-(4.4) считается решенной в классе программных управлений.

Для определения оптимального синтеза нам понадобится, помимо исходной задачи (4.1)-(4.4), семейство аналогичных ей текущих задач.

Текущую задачу ((t, x)-задачу) определим для момента t[t₀,T] и для произвольной точки xM(t) следующим образом:

(4.1')

x()M() (M(t) = x), t    T; (4.2')

u()U, t    T; (4.3')

(4.4')

Эту задачу символически обозначим (x, T – t). Ясно, что исходная задача получится из семейства {(x, T – t),  x(t)M(t),  t₀  t  T} при t = t₀, x = x⁰.

Сужение траектории и управления на [t,T] (см. рис. 4.2) будем обозначать

Как было замечено раньше (см. раздел 1), программное управление имеет существенный с точки зрения практики недостаток. Остановимся на нем более подробно. Пусть – оптимальный программный процесс.

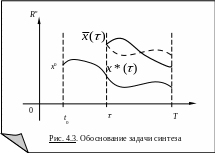
Предположим, что в момент (t₀,T) под действием внешних (непредсказуемых) возмущений нарушился запрограммированный ход управляемого процесса и система оказалась в точке (рис. 4.3). Так как программное управление распознает только время, то из состояния оно будет действовать так же, как и в состоянии . Ясно, что задачи и разные и нельзя утверждать, что управление будет оптимальным в задаче . Остается только решить задачу заново. И так действовать в каждом подобном случае. Ясно, что такое управление объектом неэффективно.

Выход из такой ситуации заключается в том, чтобы конструировать допустимое управление изначально так, чтобы оно "распознавало" не только время, но и фазовое состояние. Иначе говоря, его нужно строить в виде функции u = u(t, x), т.е. . Такие управления называются позиционными (или синтезирующими).

Определение 4.1. Оптимальным позиционным (или синтезирующим) управлением в задаче (4.1)-(4.4) будем называть управление , если для каждого (t, x)  [t₀,T]  M выполнены условия:

1. система (4.1') имеет для 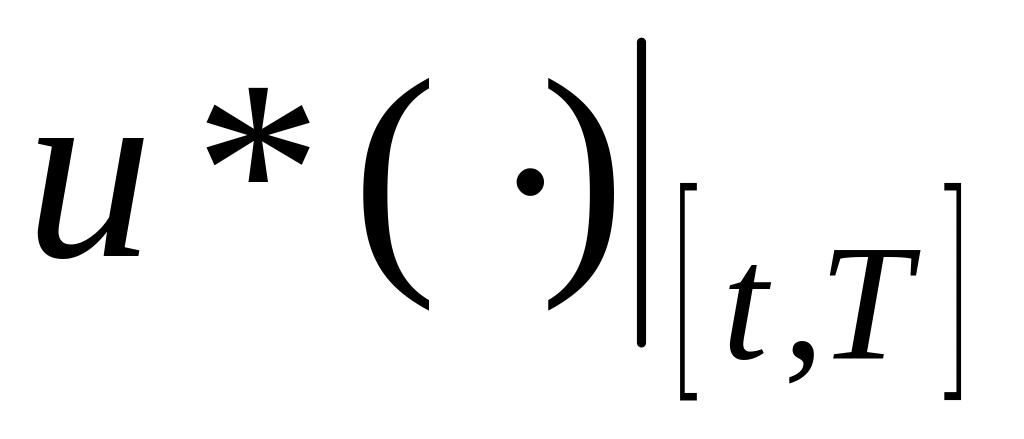единственное кусочно-гладкое решение , удовлетворяющее начальному условию и включению t    T;

2. функция времени 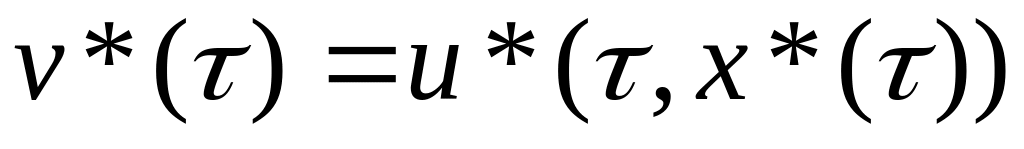кусочно-непрерывна на отрезке [t,T];

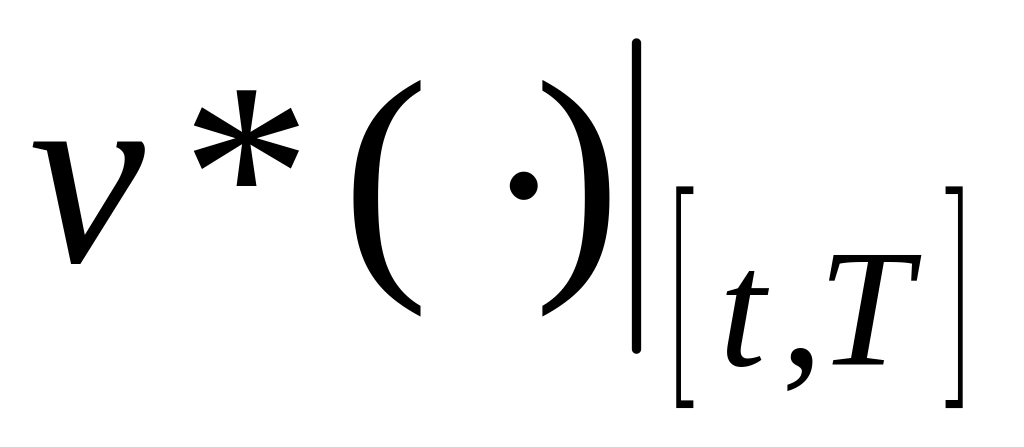
3. функция является оптимальным программным управлением в (t, x)-задаче (x, T – t).

Задачу вычисления оптимального позиционного управления будем называть задачей синтеза.

Как видно из этого определения, если в ходе управляемого процесса не происходит "незапрограммированных" изменений состояния системы, то оптимальное синтезирующее управление совпадает с оптимальным программным управлением. В случае же отклонения от оптимальной программной траектории в момент t синтезирующее управление продолжит управляемый процесс из нового состояния оптимальным образом. Для широкого класса практических задач корректировка оптимального управления в новом состоянии выполняется за короткое время, так как общий вид известен. В этом и заключается реальная ценность оптимального синтезирующего управления. Однако решение задачи (4.1)-(4.4) в классе синтезирующих управлений сложнее, чем в классе программных управлений.

Уровень сложности задачи синтеза не позволяет говорить об общих методах ее решения. В некоторых случаях оптимальное синтезирующее управление удается получить с помощью принципа максимума или метода динамического программирования. Метод динамического программирования базируется на так называемом принципе оптимальности, предложенном Р. Беллманом [4].