§9. Общая схема применения принципа максимума для вычисления оптимального управления

Схема применения принципа максимума для вычисления оптимального управления в общей задаче (3.45)-(3.49) несколько отличается от схемы для линейных систем (см. §7 раздела 2). Это связано с тем, что здесь правая часть сопряженной системы зависит от параметра управления (чего нет в линейной системе), а также для решения сопряженной системы не нужны начальные условия на вектор (t).

Пусть в задаче (3.45)-(3.49) время Т фиксировано. Тогда для вычисления оптимальных управлений (точнее, экстремалей Понтрягина – подозрительных на оптимальность управлений) нужно выполнить последовательно следующие этапы.

Этап 1. Применить центральное условие принципа максимума, т.е. решить следующую оптимизационную задачу:

(3.53)

В результате, для каждого фиксированного x и определим функцию

(3.54)

т.е. найдем общий вид экстремалей.

Этап 2. Найти экстремальные траектории прямой и сопряженной систем. Для этого нужно решить краевую задачу принципа максимума – систему из 2n уравнений

(3.55)

на отрезке [0,T] с 2n краевыми условиями

(3.56')

(3.56'')

Это дает общий вид фазовой траектории , соответствующей экстремали (3.54), и решение сопряженной системы .

Этaп 3. Установить числовое значение постоянной ₀. Доказать, что ₀  0 (это возможно, когда ₀ = 0 приводит к противоречиям), тогда ₀ = –1. Если же ₀ = 0 допустимо, то задача (3.45)-(3.49) вырожденная.

Этап 4. Вычислить окончательный вид экстремальных управлений. Для этого найденные на этапах 2 и 3 величины , ₀, , ..., подставляем в (3.54):

Для того, чтобы найденное управление было оптимальным в задаче (3.45)-(3.49), нужно:

1. чтобы 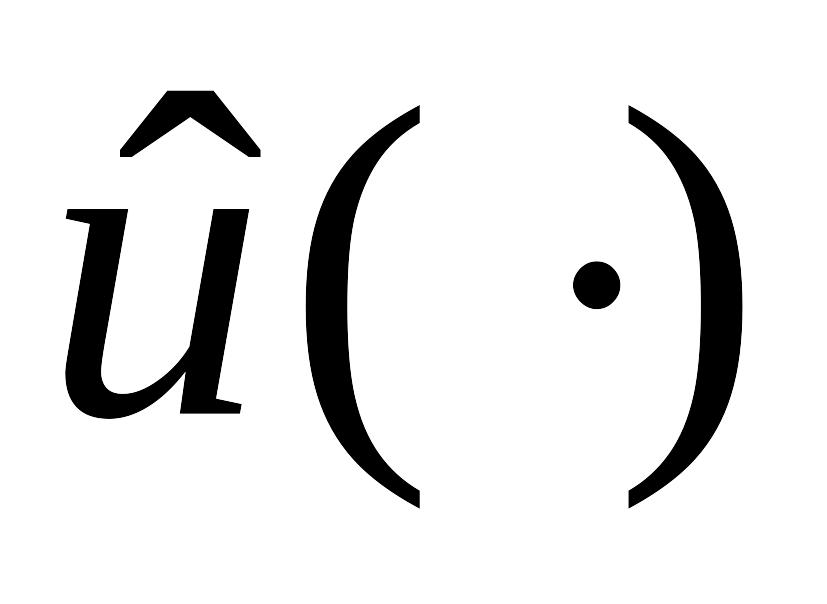было допустимым управлением, т.е. чтобы была кусочно-непрерывной функцией и для любого t ;

2. чтобы в задаче (3.45)-(3.49) существовало единственное оптимальное управление (устанавливается заранее).

Замечание. Если в задаче (3.45)-(3.49) время Т не фиксировано, то его определяют дополнительно с помощью равенства (3.51). Если не удается аналитически решить краевую задачу (3.55), (3.56') , (3.56''), то используют различные численные методы.

Для задачи (3.45)-(3.49) с подвижным правым концом приведенная выше схема отличается тем, что на этапе 2 наряду с 2n неизвестными x₁, …, x_n, ₁, …, _n остаются лишь n начальных условий (3.56'), а условия (3.56'') заменяются условиями трансверсальности (3.44). Однако условие (3.44) "приводит" еще k неизвестных ₁, …, _k. Для них краевыми условиями служат k равенств (3.43). Таким образом, на этапе 2 для вычисления 2n + k неизвестных x₁, …, x_n, ₁, …, _n, ₁, …, _k имеется 2n + k уравнений (краевых условий) (3.56'), (3.43) и (3.44).

§10. Примеры решения нелинейных задач оптимального управления с применением принципа максимума

В рассмотренных ниже примерах решение задачи оптимального управления осуществляется по приведенной в предыдущем параграфе схеме и доводится до стадии построения краевой задачи принципа максимума (объединение прямой и сопряженной систем дифференциальных уравнений (3.55) с граничными условиями на фазовые переменные (3.56'), (3.56'') и/или условиями трансверсальности). Решение этих задач получается средствами теории дифференциальных уравнений или численными методами и дает общий вид фазовых траекторий и траекторий сопряженной системы, откуда уже можно получить окончательный вид экстремальных управлений.

Пример 3.4. Рассмотрим задачу Майера

(3.57)

(3.58)

, (3.59)

где x = (x₁, x₂) – фазовые координаты, – заданная точка, T > 0 – фиксированный момент времени. Правый конец траектории в этой задаче свободен. Функция Понтрягина записывается следующим образом:

,

а сопряженная система –

(3.60)

Краевые условия для этой задачи (условия трансверсальности) принимают вид

, (3.61)

где – целевой функционал в рассматриваемой задаче Майера.

Из центрального условия принципа максимума (3.53) следует: . Тогда краевая задача принципа максимума запишется в виде

(3.62)

(3.63)

Если краевая задача (3.62), (3.63) имеет решение (0  t  T), причем обращается в ноль в конечном числе точек, то функция будет экстремальным управлением в задаче (3.57)-(3.59).

Пример 3.5. Пусть в задаче (3.57) с закрепленным правым концом x(T) = 0, когда T > 0 фиксировано, требуется минимизировать функционал .

Здесь uR¹, функция Понтрягина имеет вид

,

сопряженная система задается уравнениями (3.60).

Заметим, что в случае ₀ = 0 функция Понтрягина может достигать своей верхней грани на R¹ лишь при ₂ = 0. Но если ₂(t)  0 (0  t  T), то из второго равенства (3.60) получим ₁(t)  0, что противоречит условиям принципа максимума. Таким образом, можем считать ₀ = –1, т.е. рассматриваемая задача невырожденная. Тогда из условия (3.53) получим: . Краевая задача принципа максимума будет иметь вид

x(0) = x⁰, x(T) = 0.

Пример 3.6. Рассмотрим задачу быстрейшего перевода точки x = (x₁, x₂) из состояния x⁰  0 в начало координат (0, 0), предполагая, что движение точки подчиняется закону (3.57), (3.58).

В этой задаче конечный момент времени не фиксирован, критерий качества – интегральный с подынтегральной функцией f  ⁰  1.

Функция Понтрягина имеет вид

Отсюда ясно, что, как и в предыдущих примерах, сопряженная система будет определяться соотношениями (3.60). Из условия (3.53) вытекает общий вид экстремалей: . Краевая задача принципа максимума в этом случае будет состоять из системы (3.62), граничных условий x(0) = x⁰, x(T) = 0, условия нетривиальности вектор-функции и условия (3.51), которое в данном случае принимает вид . Отметим, что в этой задаче ₂  0. В самом деле, если бы ₂(t)  0, то из второго равенства в (3.60) следует ₁(t)  0, а из (3.51) вытекает ₀ = 0, что противоречит принципу максимума.

Задачи

1. Решить задачу быстрейшего попадания из начальной точки x⁰ = –1 в состояние x¹ = 0 для системы, заданной уравнением с ограничением .

2. Решить задачу оптимального быстродействия:

,

,

,

,

.

3. Найти минимум функционала , если , , , x(1) = 1. Показать, что – оптимальное управление, и убедиться в том, что в принципе максимума здесь надо принять (т.е. рассматриваемая задача оптимального управления – вырожденная).

4. Уравнения движения тела, движущегося со скоростью, модуль которой равен 1, имеют вид где u – управление, причем Поставлена задача переноса тела из начального состояния , , в состояние , за минимальное время T. Вычислить экстремальные управления для этой задачи.

5. Решить задачу быстрейшего попадания в начало координат для объекта, заданного системой с ограничениями . В качестве начального состояния взять точку (2, 0).