§6. Принцип максимума в автономных задачах с закрепленными концами

Рассмотрим задачу Лагранжа с нефиксированным моментом окончания Т > 0:

(3.32)

x(0) = x⁰, (3.33)

u(t)  U, 0  t  T, (3.34)

x(T) = x¹ (T – нефиксировано), (3.35)

(3.36)

В качестве допустимых управлений будем рассматривать кусочно-непрерывные функции вида u = u(t). Функции f и f ₀ предполагаются непрерывными по всем своим переменным и непрерывно дифференцируемыми по x₁, …, x_n.

Функция Понтрягина в этой задаче имеет вид:

.

Введем (n +1)-мерные векторы , . Тогда мы можем написать:

(3.37)

В (3.37) ₀ = const, а ₁ = ₁(t), ..., _n = _n(t) являются решениями уравнений

(3.38)

или в векторной форме:

Система (3.38) называется сопряженной (к (3.32)) системой, так как справедливо представление:

Как и в линейном случае, нас будут интересовать лишь нетривиальные решения системы (3.38), так как при _i  0, i = 1, ..., n, теряется смысл введения функции Понтрягина (теряются "ограничения" – уравнения динамики).

Принцип максимума для задачи (3.32)-(3.36) сформулирован в следующей теореме.

Теорема 3.8. Пусть – оптимальный программный процесс в задаче (3.32)-(3.36) с нефиксированным временем T. Тогда существуют непрерывные функции , ..., и постоянное число , удовлетворяющие следующим условиям:

1. вектор 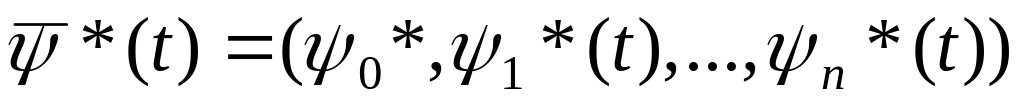является ненулевым для любого t[0,T];

2. вектор 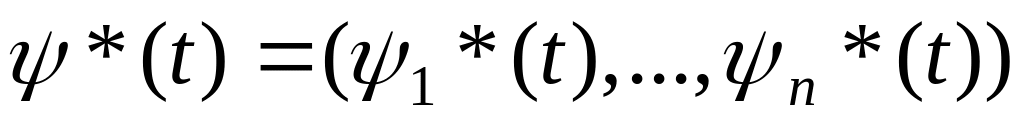является решение системы (3.38);

3. для каждого фиксированного t[0,T] функция 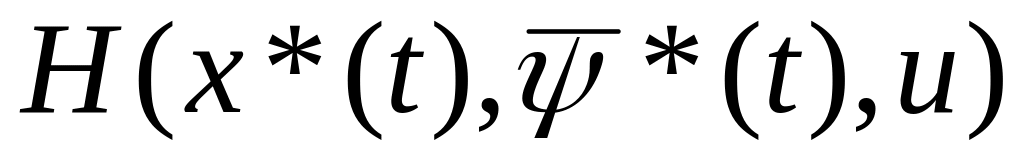достигает максимума в точке 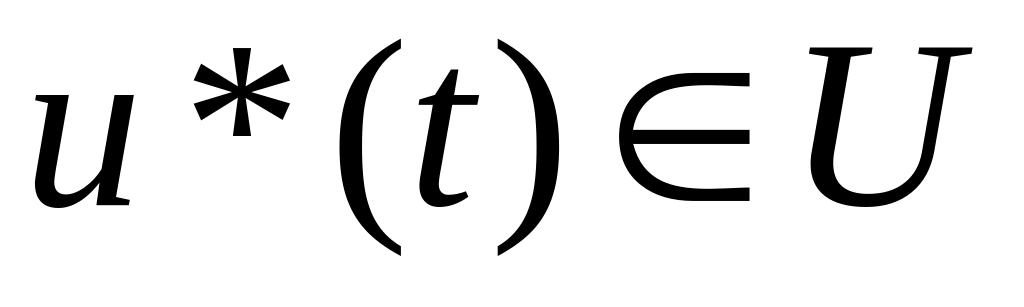, т.е.

(3.39)

4. для каждого t[0,T] выполняется равенство

. (3.40)

Кратко поясним условия теоремы. Главным является условие (3.39), которое и есть принцип максимума для (3.32)-(3.36). Видим, что здесь принцип максимума является необходимым условием оптимальности.

Относительно возможны два случая: а) или б) . В случае а) в функции Понтрягина не учитывается функционал качества f ₀, т.е. получается, что необходимые условия оптимальности не зависят от вида функционала качества. Такие задачи называются вырожденными. Если удается доказать, что , то . Оказывается, что в этом случае всегда можно положить (а в задаче на максимум ), так как это не нарушит условий (3.38), (3.39), (3.40).

Условие 4) – это следствие нефиксированности времени T прихода в целевую точку x ¹. Практически равенство (3.40) применяется для определения этого момента T. Фактически же для и , удовлетворяющих условиям (3.38) и (3.39), оказывается для каждого t[0,T]. Поэтому условие (3.40) можно проверить в любой момент t.

Если заранее известно о существовании единственного оптимального управления в задаче (3.32)-(3.36), теорема 3.8 дает необходимое и достаточное условие оптимальности.

Предположим теперь, что в задаче (3.32)-(3.36) время окончания T фиксировано, т.е. с самого начала требуется прийти в точку x ¹ к моменту T с минимизацией функционала (3.36).

Чтобы получить принцип максимума для этой задачи из теоремы 3.8, приведем новую задачу к задаче с нефиксированным временем. Для этого к n фазовым переменным x₁, …, x_n добавим (n +1)-ую переменную x_n+1 из условия: x_n+1(t)  t (для любого t). Тогда , x_n+1(0) = 0. Таким образом, время t мы ввели в число фазовых координат. В расширенном фазовом пространстве Rⁿ⁺¹ динамика системы с нефиксированным временем запишется

т.е. из точки (x ⁰, 0) надо перейти в точку (x ¹,T) с минимизацией функционала (3.36). Так как такой переход автоматически обеспечивает время T, то время окончания процесса управления можно считать нефиксированным.

Функция Понтрягина в новой задаче имеет вид:

где H имеет вид (3.37). Поэтому принцип максимума (3.39) запишется:

т.е. принцип максимума (3.39) в новой задаче остается без изменения. Иначе говоря, функция в формулировке необходимого условия оптимальности не принимает участия.

Условие (3.40) теоремы 3.8 в новой задаче принимает вид:

. (3.41)

Так как не принимает участия в необходимом условии, то это условие теряет смысл в новой задаче и его надо отбросить.

Сопряженная система для новой задачи запишется:

По той же причине (n +1)-ое уравнение здесь надо отбросить.

В результате приходим к следующему утверждению.

Теорема 3.9. Пусть – оптимальный программный процесс в задаче (3.32)-(3.36) с фиксированным временем окончания T. Тогда существуют нетривиальные вектор-функции , ..., и число такие, что выполнены условия 1)-3) теоремы 3.8.

Единственным отличием теоремы 3.9 от теоремы 3.8 является отсутствие условия (3.40), применяемого для определения момента Т, что в новой задаче не нужно.