§5. Принцип максимума в задачах с терминальным функционалом качества

Рассмотрим следующую задачу Майера:

, , (3.20)

, (3.21)

, , (3.22)

. (3.23)

Относительно функции f будем предполагать, что она непрерывна в и имеет непрерывные частные производные по x; множество U компактно в , а функция F непрерывна в и имеет непрерывные частные производные по x.

Задачу (3.20)-(3.23) будем рассматривать в классе кусочно-непрерывных функций: . Таким образом, задача заключается в нахождении такого управления , для которого в конце траектории функция F достигает минимального значения.

Как и в линейном случае, принцип максимума формулируется с помощью так называемой сопряженной системы и скалярного произведения ее решения на правую часть системы (3.20). Это скалярное произведение называется функцией Понтрягина (или Гамильтона):

, (3.24)

где – решение сопряженной системы вида

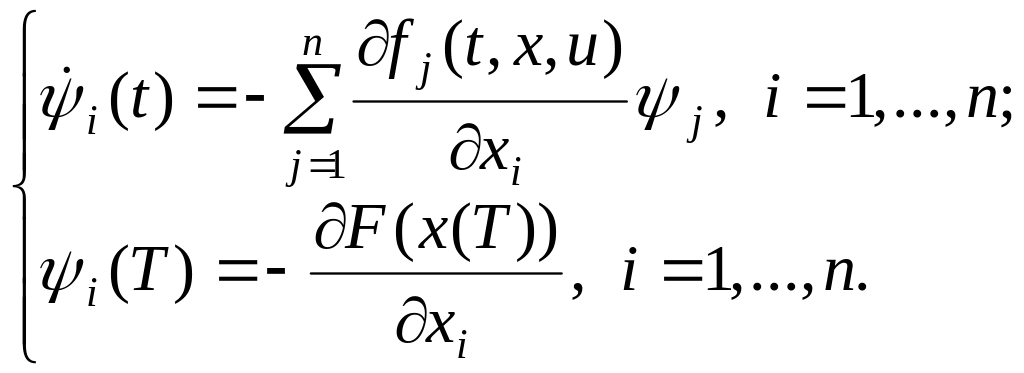(3.25)

С помощью функции Понтрягина уравнения (3.20) и (3.25) можно записать в виде

, .

Для доказательства теоремы о принципе максимума в задаче (3.20)-(3.23) нам будут нужны понятия приращения критерия качества (3.23) и приращения допустимого управления (игольчатой вариации).

Рассмотрим два допустимых управления , , где для каждого , и соответствующие им траектории , (для каждого ). Найдем формулу для приращения критерия качества:

.

Это равенство можно записать в следующем виде:

.

Приращение траектории удовлетворяет дифференциальному уравнению

, ,

,

которое можно записать так:

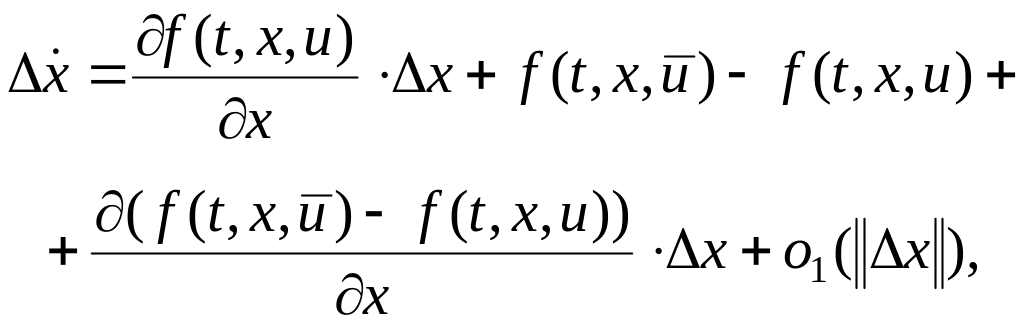(3.26)

.

Обозначим

.

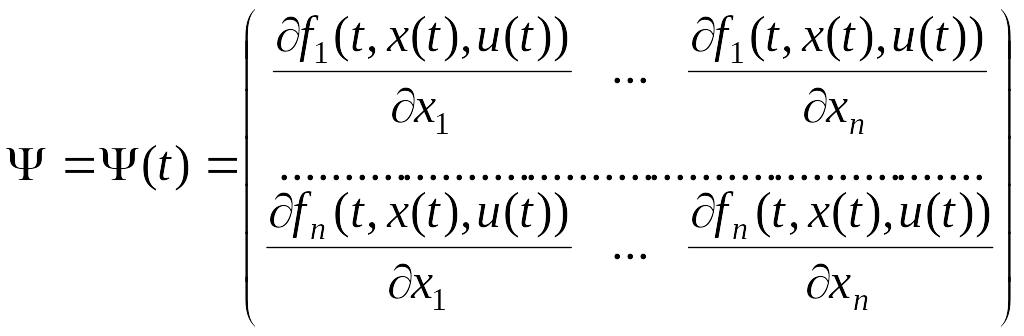Пусть -матрица Y(t) есть решение уравнения

, ,

где E – единичная диагональная -матрица.

Стандартными рассуждениями теории дифференциальных уравнений можно показать, что уравнение (3.26) эквивалентно интегральному уравнению

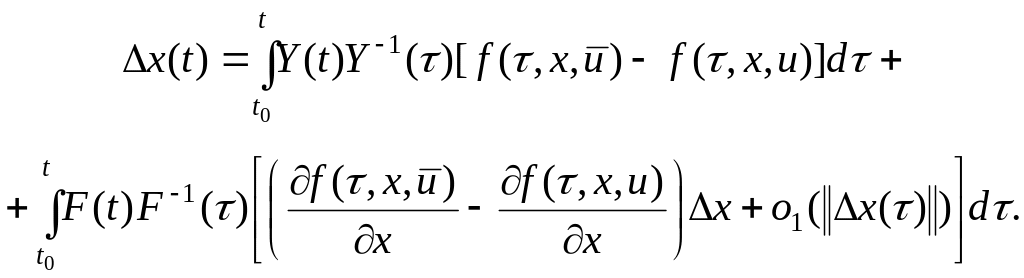
Поэтому можно записать:

.

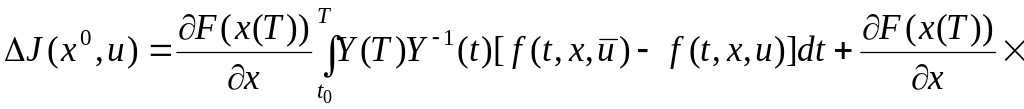
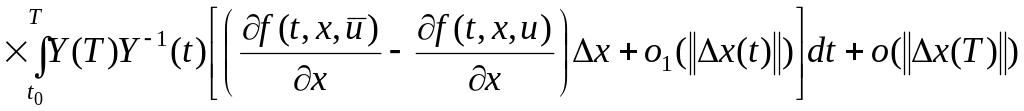Можно показать, что

.

Тогда из последнего выражения получаем:

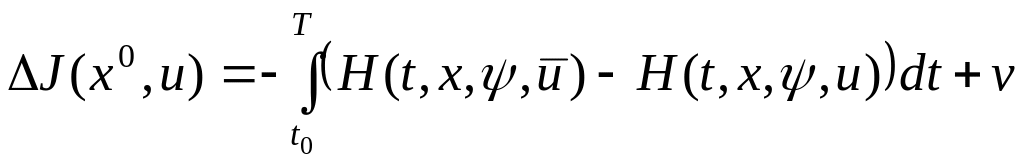, (3.27)

где , ,

, .

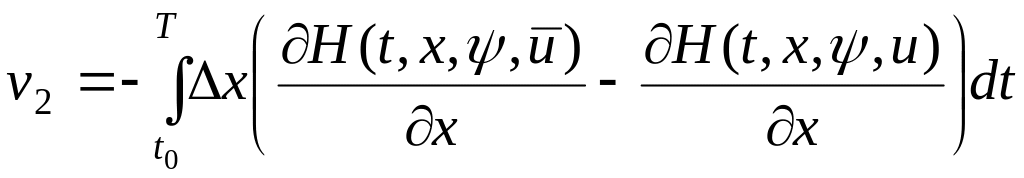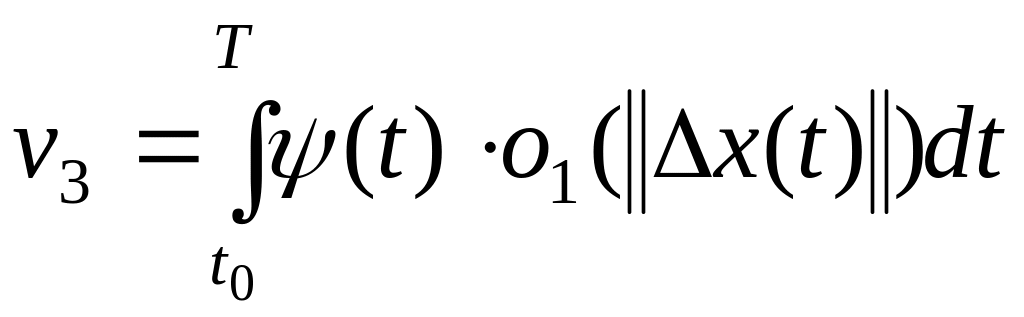Рассмотрим теперь приращение управления. Игольчатой вариацией называется приращение вида

(3.28)

где , , . При малых  траектория , порожденная игольчатой вариацией, мало отличается от траектории , порожденной управлением без вариации. Поэтому без дополнительного доказательства примем, что

, , (3.29)

где достаточно мало.

Теорема 3.6. Пусть – оптимальный программный процесс в задаче (3.20)-(3.23). Тогда существует нетривиальное решение сопряженной системы (3.25), удовлетворяющее условию

(3.30)

для всех .

Доказательство. Пусть – оптимальное управление, а , – соответствующие траектории систем (3.20) и (3.25). Предположим, что равенство (3.30) неверно. Тогда при некоторых и

Проварьируем управление игольчатой вариацией (3.28) и вычислим по формуле (3.27) приращение функционала качества:

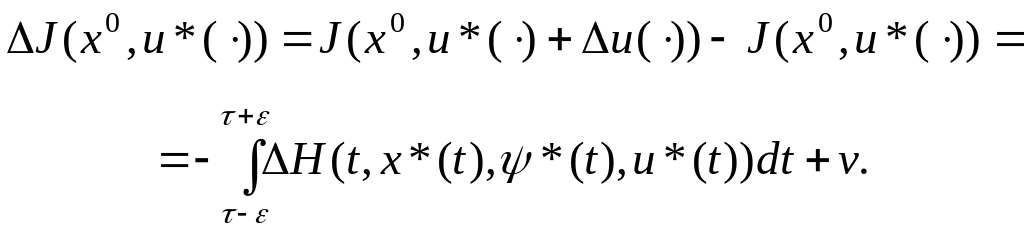(3.31)

С учетом (3.28) и (3.29) получаем:

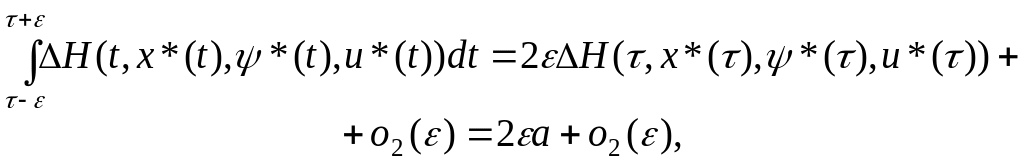
где , , , , а – число, участвующее в оценке вида (3.29) (аналог числа ) на отрезке , . Подставив эти оценки в (3.31), приходим к неравенству

,

которое при достаточно малых принимает вид . Полученное противоречие к определению оптимальности управления доказывает теорему.

Равенство (3.30) называется принципом максимума в задаче (3.20)-(3.23). Как видно из теоремы, он является необходимым условием оптимальности первого порядка, так как содержит производные не выше первого порядка. Оказывается, этот принцип является самым сильным из известных необходимых условий оптимальности первого порядка, поскольку последние следуют из него. Однако в общем случае равенство (3.30) не является достаточным для оптимальности, т.е. не каждое управление, удовлетворяющее равенству (3.30), является оптимальным.

Пример 3.3. Рассмотрим следующую задачу терминального управления на :

, ;

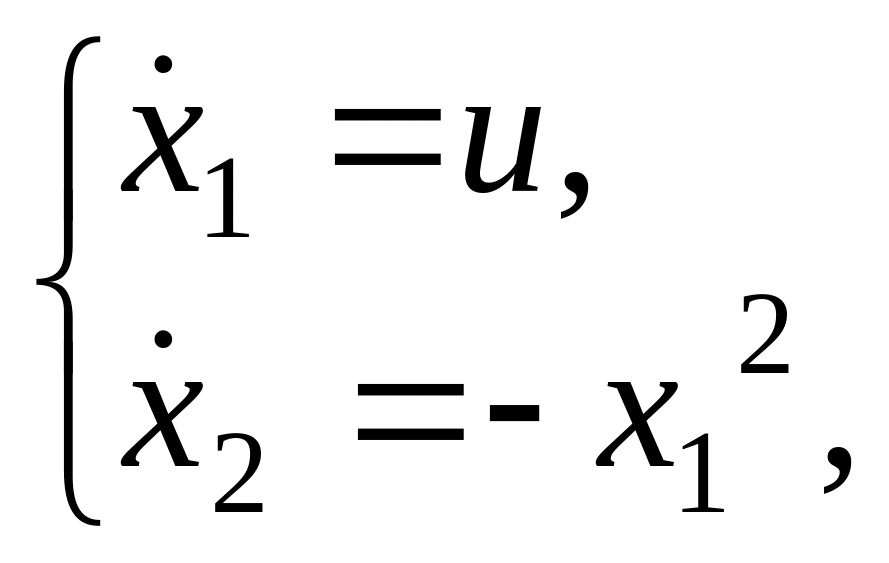
Функция Понтрягина и сопряженная система имеют вид:

;

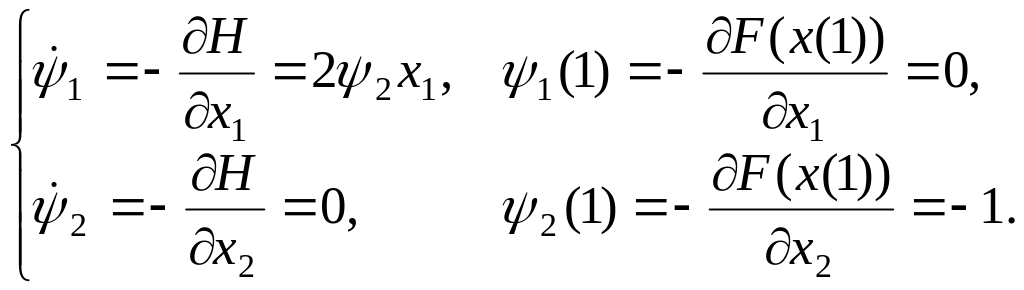
Отсюда имеем:

, , .

Построим допустимое управление :

Для такого управления первая компонента траектории принимает вид

Видно, что , поэтому удовлетворяет принципу максимума. Но оно не является оптимальным, ибо

,

а, например, для допустимого управления .

В задаче (3.20)-(3.23) на траектории не наложены условия справа. Предположим теперь, что требуется привести траекторию системы (3.20) из точки в предзаданное множество к моменту T с минимизацией функционала (3.23). Предположим также, что множество задано соотношениями

Будем считать, что функции непрерывны в .

Принцип максимума для задачи с подвижным во множестве правым концом траектории отличается от приведенной выше теоремы тем, что в момент T требуется ортогональность вектора к опорной гиперплоскости, проведенной в точке (условие трансверсальности).

Теорема 3.7. Пусть – оптимальный программный процесс в задаче (3.20)-(3.23) с терминальным множеством . Тогда существует ненулевой вектор такой, что вдоль траектории сопряженной системы (3.25) выполняются условия

1. , , ;

2. ;

3. , ,

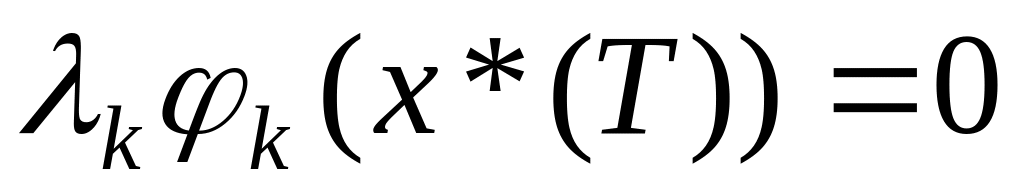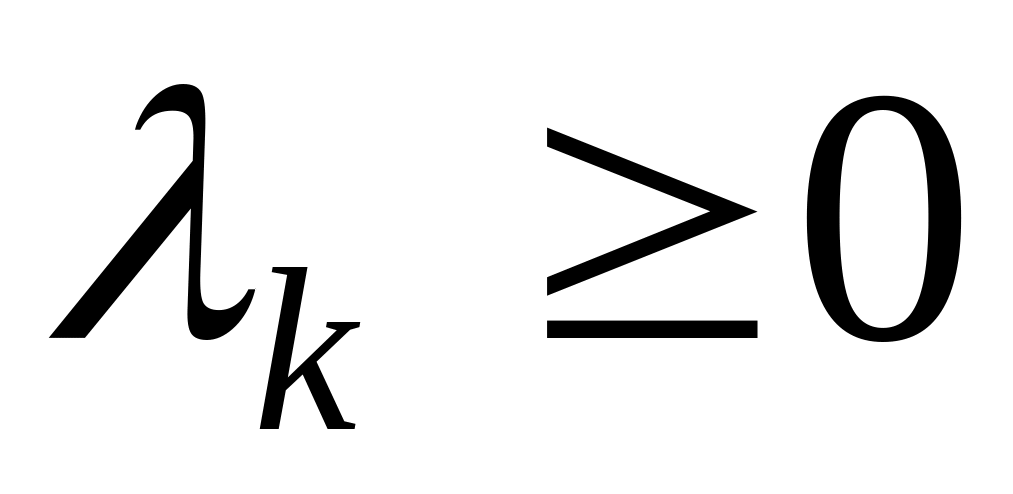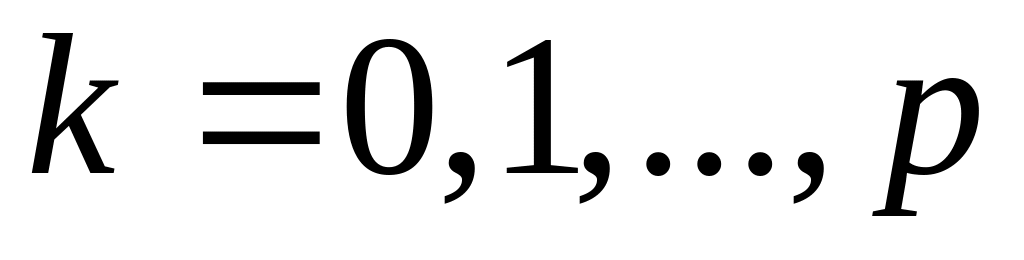где .

Вывод условия трансверсальности 2), а также условия 1) (дополняющей нежесткости) мы покажем в §7 этого раздела.