§4. Существование оптимального управления в задачах Больца и Лагранжа

Задачу Больца поставим в следующей общей форме:

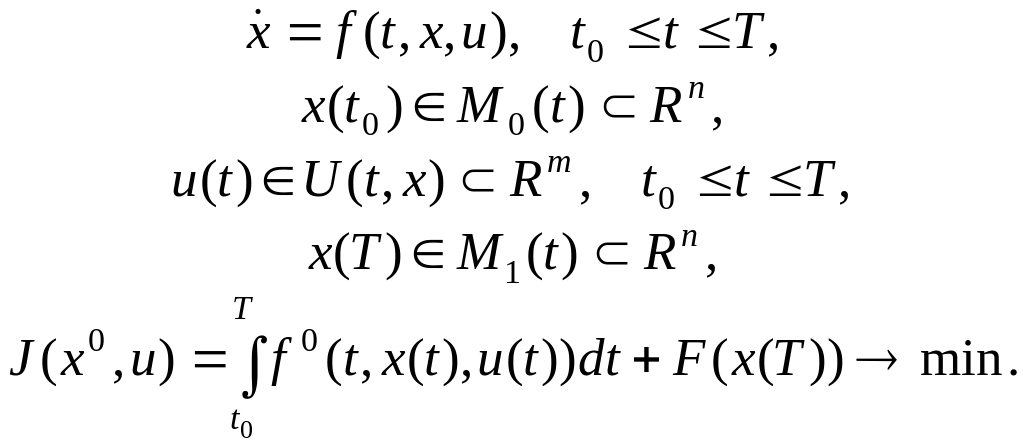(3.13)

Задача (3.13) рассматривается в том же классе допустимых управлений , что и задача (3.4).

Множество обобщенных скоростей определим следующим образом: для каждого состояния

.

Теорема 3.3. Пусть в задаче (3.13) выполнены следующие условия:

1. условия 1)-4) и 8) (для ) теоремы 3.1;

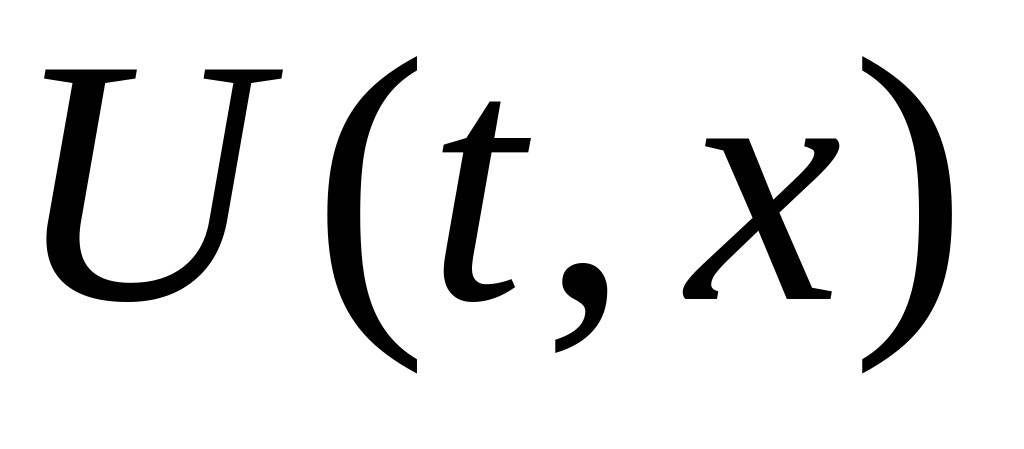2. – непустое, компактное для каждого в и непрерывное в 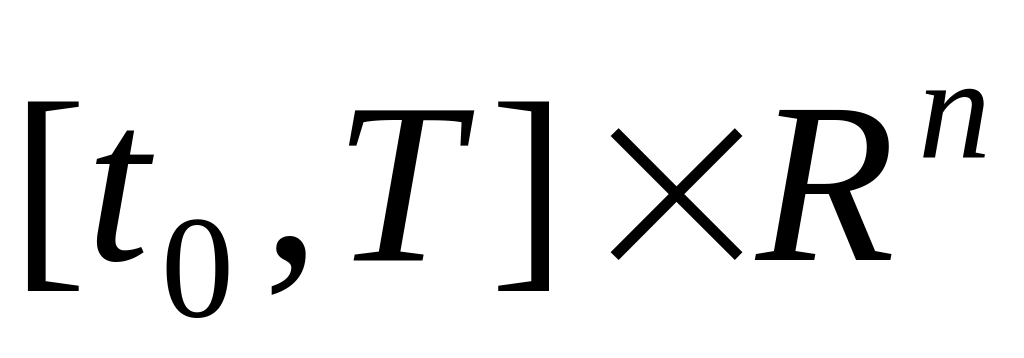множество;

3. M₀(t) и M₁(t) – непустые, компактные для каждого в Rⁿ и непрерывные на [t₀,T] множества;

4. f ⁰ – скалярная непрерывная по всем переменным (т.е. в ) функция;

5. F – непрерывна в Rⁿ.

Тогда в задаче (3.13) существует оптимальное управление

Ввиду ограниченности объема учебного пособия, доказательство этой теоремы приводить не будем. Доказательство, построенное по схеме доказательства теоремы 3.1, можно найти в [36], стр. 97. Другой способ доказательства теоремы 3.3 может состоять в сведении задачи Больца (3.13) к задаче Майера (3.4). Для этого введем дополнительную фазовую переменную из условий

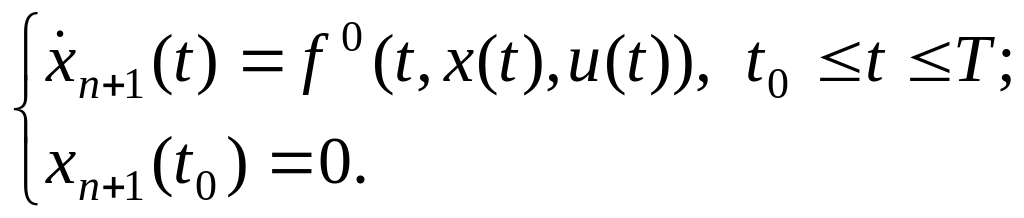(3.14)

Отсюда для каждого

.

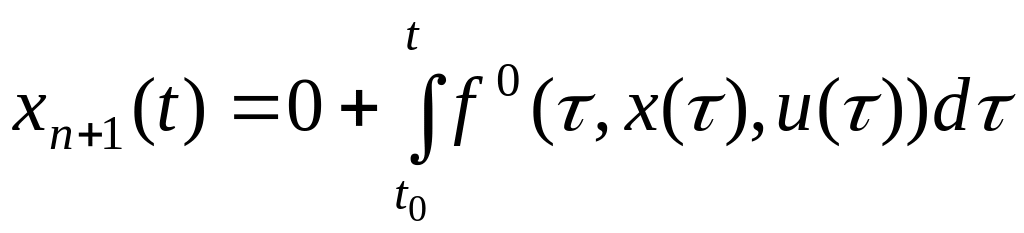Следовательно, функционал качества в задаче (3.13) можно представить в виде

,

где . В итоге задача Больца (3.13) получит следующую форму (задачи Майера):

;

,

;

,

в фазовом пространстве ( ), где , , , .

Если в построенной таким образом задаче Майера существует оптимальное управление (см. теорему 3.1), то оно существует и в исходной задаче Больца (3.13).

Если , то задача (3.13) превращается в задачу Лагранжа. Нетрудно видеть, что преобразование (3.14) превращает задачу Лагранжа в задачу Майера.

Теорема 3.4. Пусть в задаче Лагранжа, которая получается из (3.13) при , выполнены условия a)-d) теоремы 3.3. Тогда в задаче Лагранжа существует оптимальное управление

Заметим также, что для перехода от задачи Майера к задаче Лагранжа достаточно использовать преобразование

Следовательно, ( ). Положим , . Тогда

,

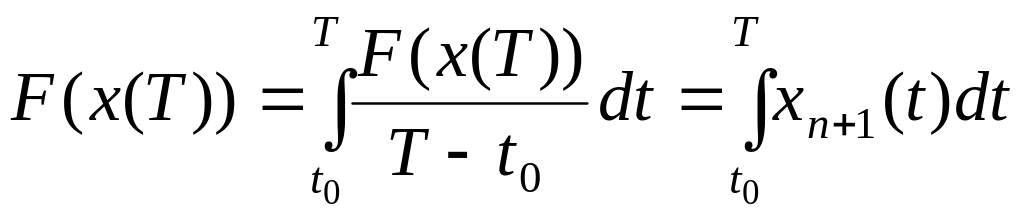и мы получили задачу Лагранжа с функционалом

.

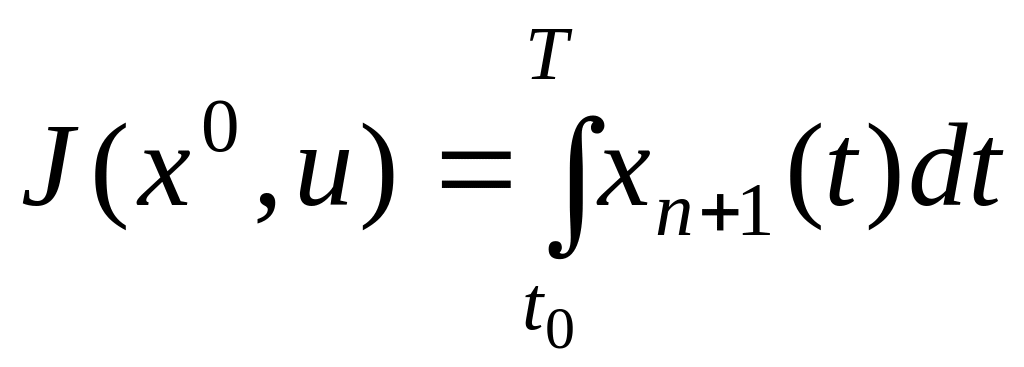В завершение параграфа приведем еще одну теорему существования для нелинейной задачи Лагранжа, в которой нет ограничений на управляющие параметры вида , т.е. когда .

Рассмотрим задачу

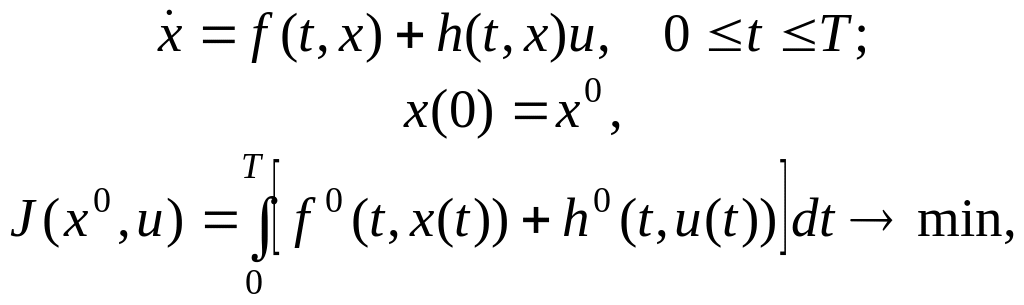(3.15)

где f, h, f ⁰, h ⁰, вообще говоря, нелинейные функции.

Под допустимым управлением понимается любая функция , которая вместе с соответствующей траекторией доставляет критерию качества конечное значение.

Здесь – пространство измеримых на интервале функций с нормой

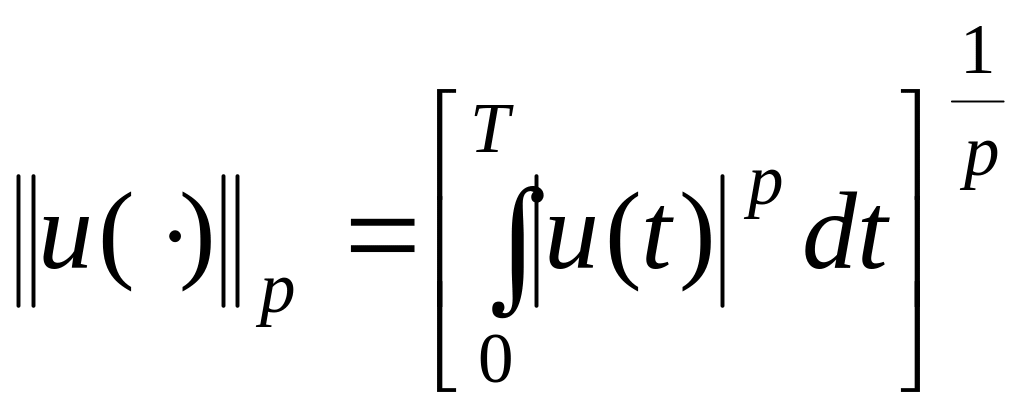, . (3.16)

Из неравенства Гельдера (см. §1) получаем:

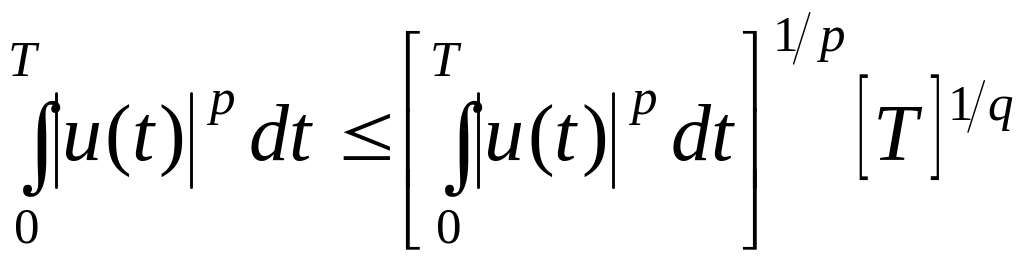, . (3.17)

Поэтому, введя норму

, (3.18)

считаем, что каждое допустимое управление принадлежит пространству .

Теорема 3.5. Пусть в задаче (3.15) выполнены следующие условия:

1. f, h, f ⁰, h ⁰ – непрерывные по 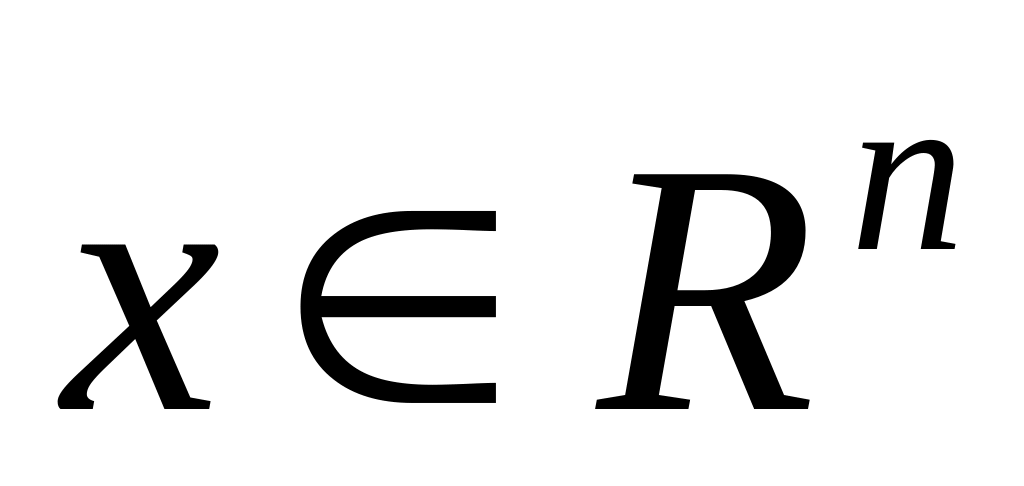, , 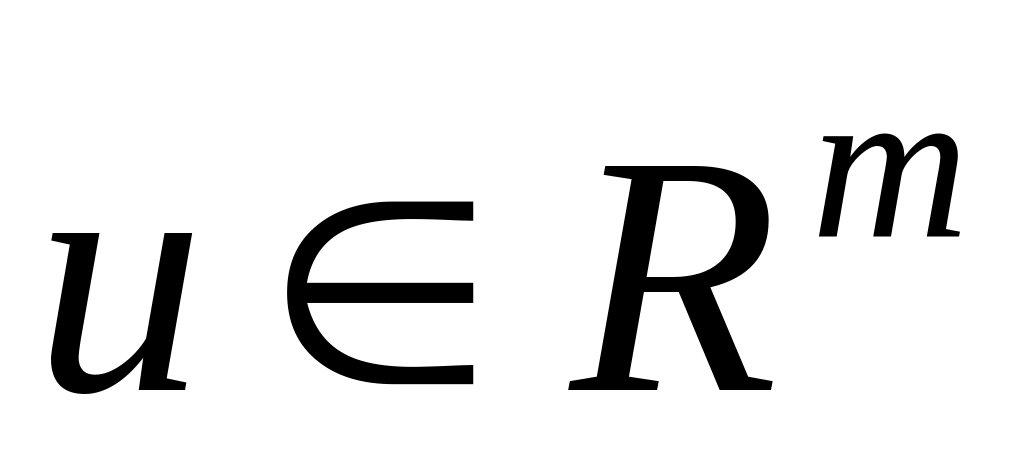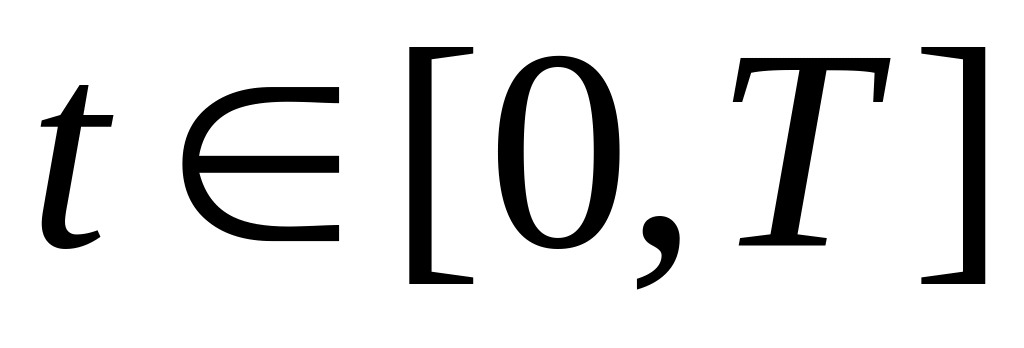функции;

2. f, h непрерывно дифференцируемы по x;

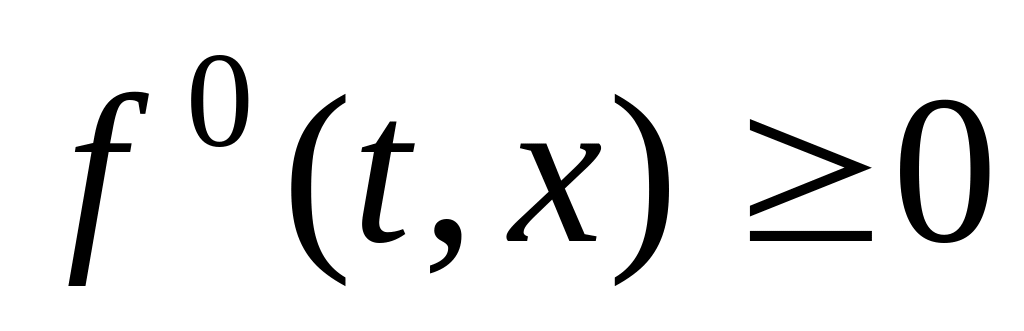3. для каждого ;

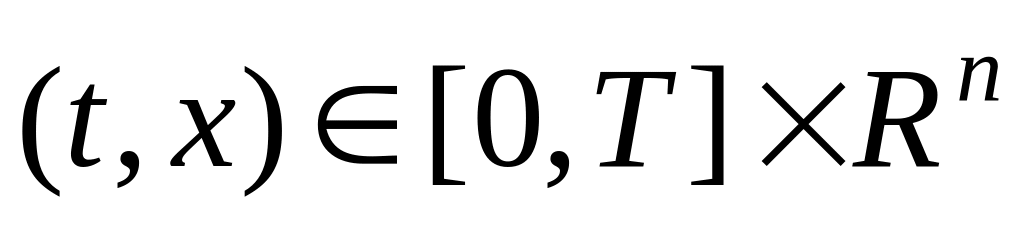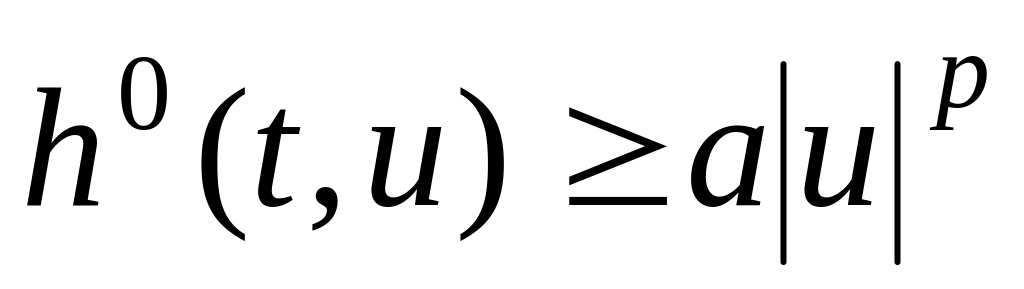4. для каждого 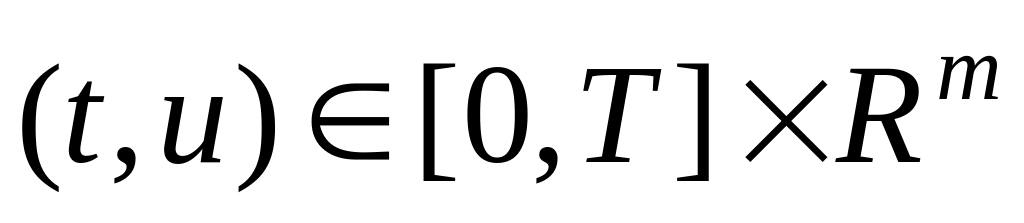, где 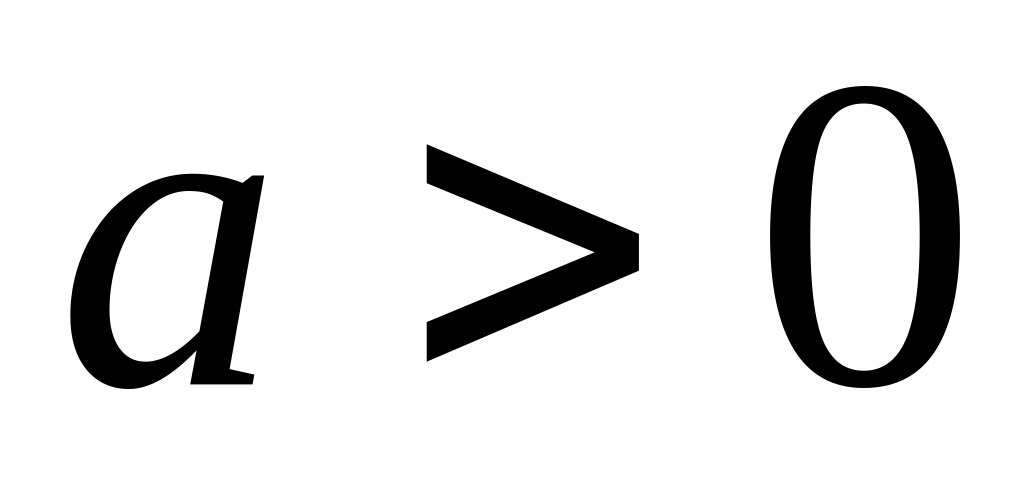, 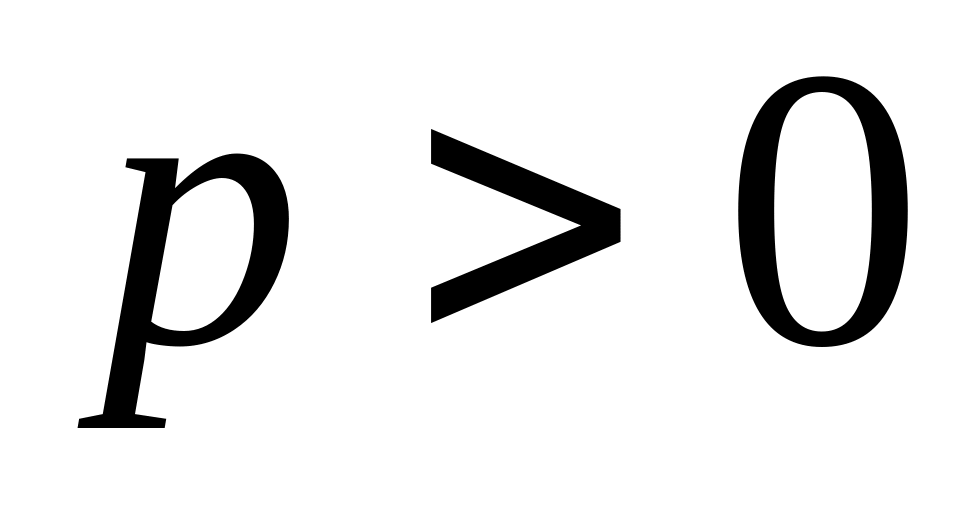– постоянные числа;

5. h ⁰ выпукло по u при любом ;

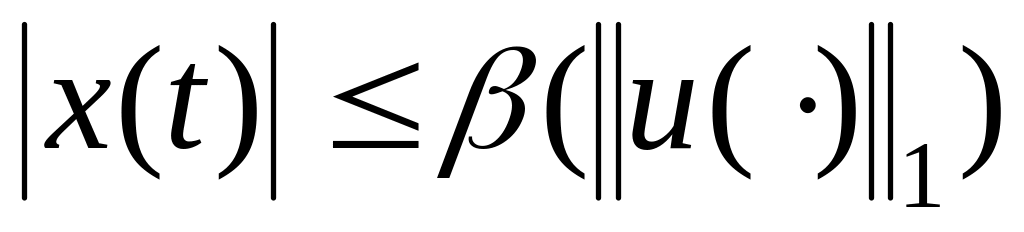6. , где 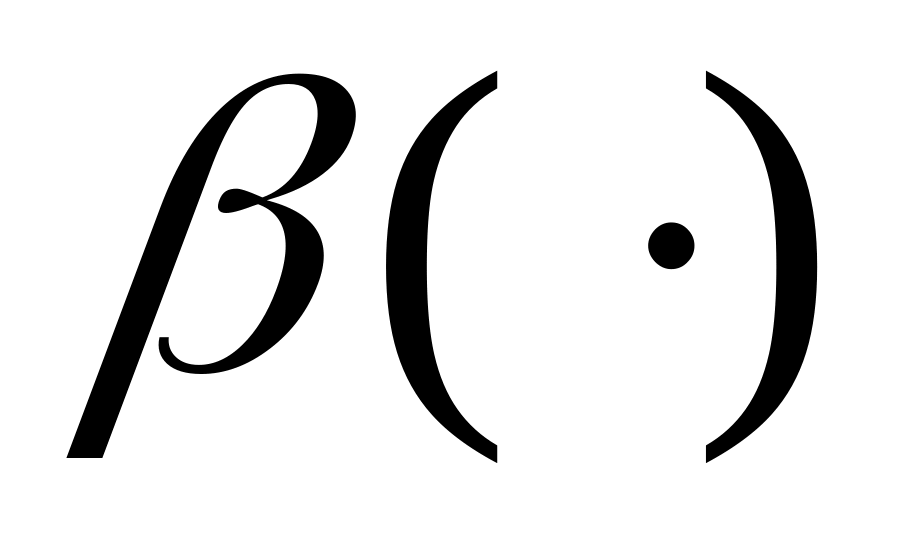– монотонно возрастающая функция .

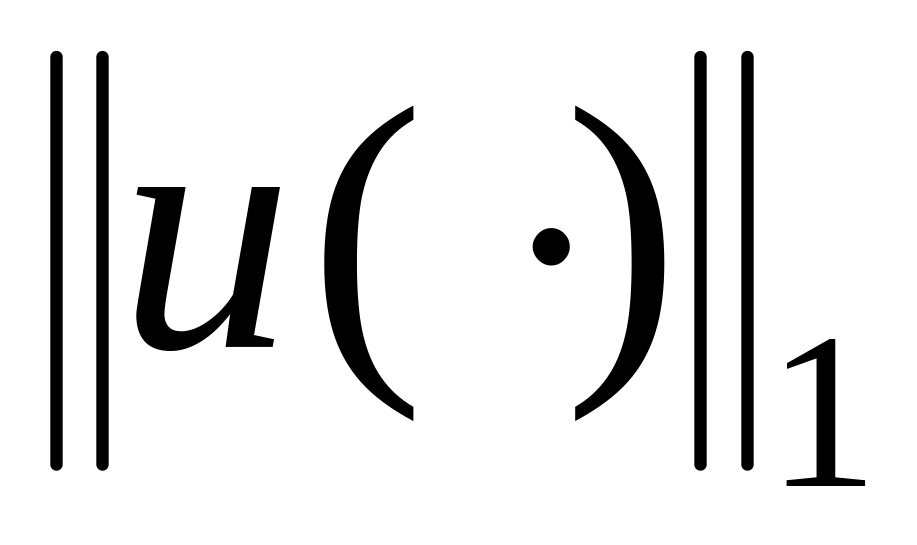Тогда в задаче (3.15) существует оптимальное управление .

Доказательство. Из условий 3) и 4) следует , поэтому существует неотрицательная нижняя грань m значений . Пусть – последовательность допустимых управлений таких, что при . Тогда можно написать для любого . Следовательно (см. условия 4) и 3)),

для достаточно больших k. Поэтому можно выбрать подпоследовательность , которая сходилась бы к некоторому пределу и такую, что

. (3.19)

Из (3.16)-(3.18) получаем:

,

где . Поэтому все траектории равномерно ограничены:

.

Для любых имеем оценку

.

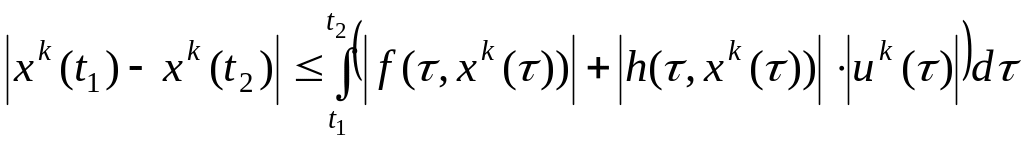Таким образом, существует постоянная , не зависящая от k, для которой

.

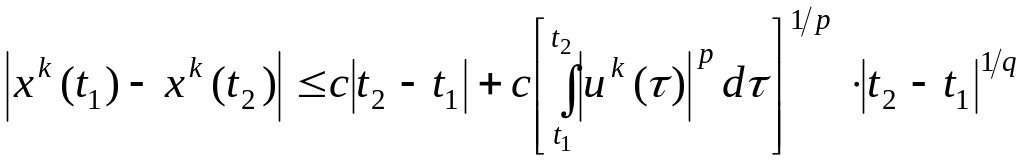Здесь c – наибольшая из неотрицательных нижних граней и (см. условия 3), 4)). Применяя (3.19), из последнего неравенства получаем:

.

Следовательно, семейство функций является равностепенно непрерывным на интервале .

Из теоремы Асколи следует, что можно выбрать подпоследовательность так, что

при каждом .

Покажем, что траектория порождена управлением . Распишем последнее равенство:

.

По определению пределов и имеем равномерно выполняющиеся равенства:

,

,

.

Пользуясь этими равенствами и равенством (3.17), написанным для , можно доказать, что

.

Отсюда следует, что

,

т.е. есть траектория, порожденная управлением .

Для минимизирующей последовательности и ее предела справедливо

.

Из этого неравенства и из выпуклости по u следует, что

.

Следовательно, и есть оптимальное управление в задаче (3.15). Теорема доказана.