§2. Задача Майера: постановка и обсуждение

Неавтономная задача Майера ставится следующим образом:

, ,

,

, , (3.4)

,

.

Таким образом, из любой точки множества M₀ требуется перевести систему в любую точку множества M₁ так, чтобы вдоль траектории функционал J принимал минимальное значение.

Так как время прихода траектории во множество M₁ для разных управлений разное, то момент T здесь не фиксирован. Существование оптимальных управлений в задаче (3.4) будем исследовать в классе измеримых по Лебегу на функций, определенных на множестве U. Таким образом, . Будем предполагать .

Напомним, что оптимальным в задаче (3.4) называется управление :

.

Если минимум не достигается, т.е. оптимальное управление не существует, то в практических задачах в качестве приближенного решения задачи (3.4) можно рассматривать любую минимизирующую последовательность :

.

Минимизирующая последовательность всегда существует и любая подпоследовательность минимизирующей последовательности будет также минимизирующей.

Пример 3.1. Пусть в (3.4) и

;

,

,

,

,

т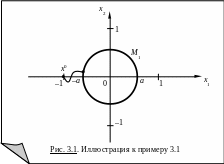 .е. требуется привести систему из заданной точки в окружность M₁ за минимальное время (рис. 3.1). Так как наибольшее значение правой части первого уравнения движения есть , то для любого управления . Как составляющая скорости по оси от точки x⁰ до окружности M₁, (T – время достижения M₁). Отсюда получаем, что для всех траекторий . Построим последовательность :

.

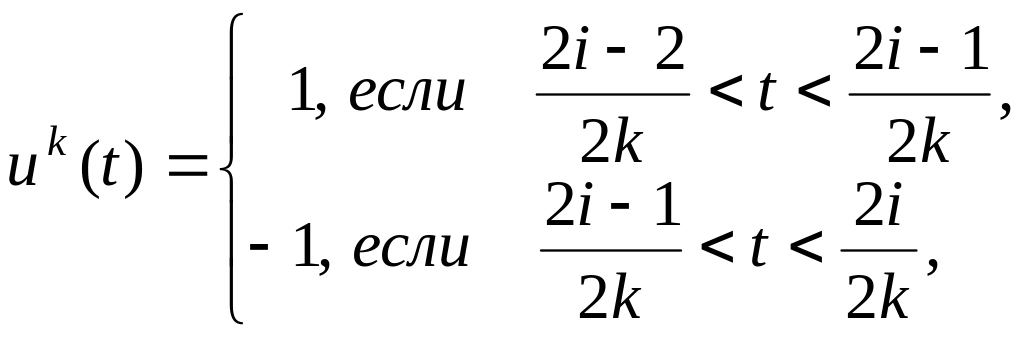
Можно показать, что . Тогда и

.

Следовательно, есть минимизирующая последовательность, а – минимальное время достижения множества M₁. Однако в этой задаче не существует управления такого, что (относительно причины отсутствия оптимального управления см. замечание после доказательства теоремы 3.1).

Пример 3.2. Пусть в (3.4) и

, ;

,

,

,

.

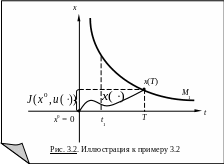Очевидно, для любого (рис. 3.2).

Покажем, что J не достигает минимума ни на одном допустимом управлении. Построим допустимое управление:

где t₁ – произвольный момент, T – первый момент попадания траектории в M₁: . По определению имеем – координата точки прихода в терминальное множество M₁ при управлении (т.е. по траектории ). Очевидно, . Поэтому, взяв t₁ достаточно большим, т.е. достаточно долго "удержав" систему в начале координат, можно приблизить значение сколь угодно близко к нулю:

.

Однако здесь нет допустимого управления, доставляющего критерию качества это наименьшее значение. Причина отсутствия оптимального управления – в некомпактности терминального множества (здесь точнее – в асимптотическом характере M₁).

В задаче (3.4) будем предполагать, что f непрерывна в , U компактно в , M₀ и M₁ компактны в , F непрерывна на M₁. Однако, как суперпозиция измеримой функции , f становится измеримой по t на . Поэтому решением задачи Коши для каждого допустимого управления будет абсолютно непрерывная на функция

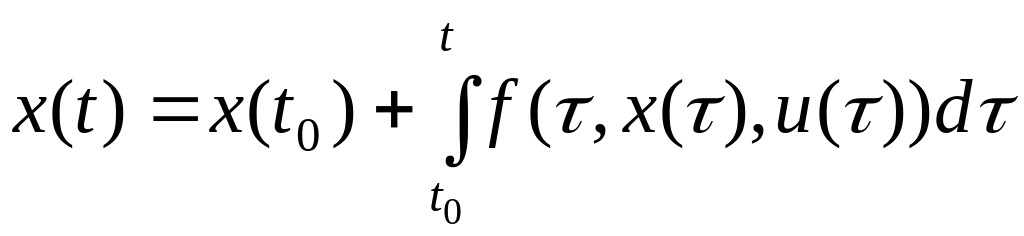. (3.5)

Производная абсолютно непрерывной функции существует почти всюду на .

Функция однозначно определяется управлением и точкой , если (см. теорему Каратеодори в §1) существуют положительные постоянные k₁ и k₂ такие, что для всех , и выполнены условия

, (3.6)

. (3.7)

Из (3.5) и (3.6) имеем:

.

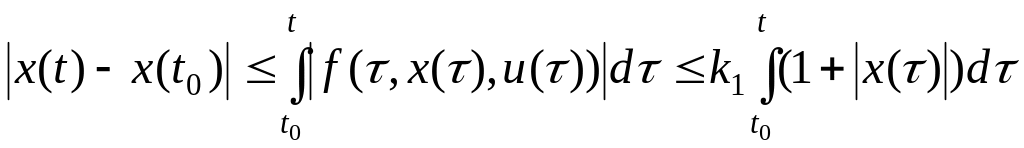Обозначим . Очевидно, . Поэтому

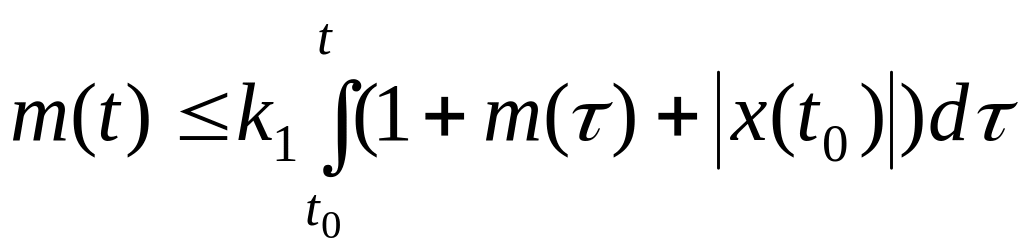
или

.

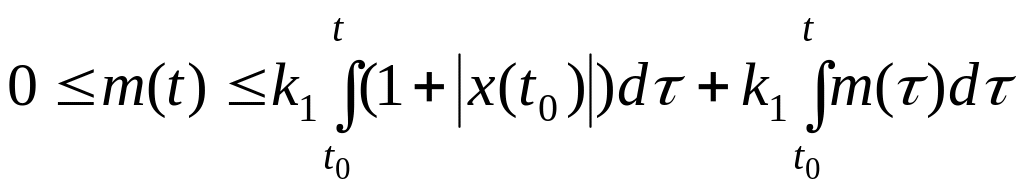Используя неравенство Гронуолла (3.3), отсюда получаем оценку

, (3.8)

где .

Для каждой фиксированной пары определим множество

, (3.9)

называемое множеством обобщенных скоростей в задаче (3.4). Оно является образом в множества при отображении . Поэтому и в силу непрерывности f по u, и компактности U множество компактно. В случае линейности f по u ( ) и выпуклости U (например, многогранник) множество выпукло.