§8. Примеры решения линейных задач оптимального управления с применением принципа максимума

Пример 2.2. Пусть дано уравнение , где u – скалярный управляющий параметр, подчиненный условию . Введя фазовые координаты x₁ = x, , это уравнение можно переписать в виде следующей системы:

, . (2.23)

Рассмотрим задачу о быстрейшем попадании фазовой точки, движущейся по закону (2.23), из заданного начального состояния x⁰ в начало координат (0,0). Иначе говоря, мы будем рассматривать задачу об оптимальном быстродействии в случае, когда конечным положением служит начало координат: x¹ = (0, 0).

В рассматриваемой задаче множество – ограниченный замкнутый многогранник (отрезок), причем 0int U. Условие общности положений заключается в линейной независимости векторов B, AB. Так как , , то это условие, очевидно, выполняется. Значит, по теореме 2.8, принцип максимума будет не только необходимым, но и достаточным условием оптимальности, и всякое экстремальное управление будет оптимальным.

Пользуясь приведенной в предыдущем параграфе схемой, найдем решение задачи.

На первом этапе определим решение сопряженной системы уравнений, которая в данном случае имеет вид

, . (2.24)

Отсюда ₁ = C₁, ₂ = C₂ – C₁t (здесь C₁, C₂ – постоянные).

Теперь, согласно этапа II, мы можем найти оптимальное управление. Максимизируя по u выражение

на множестве –1  u  1, получаем:

u*(t) = sign ₂(t) = sign (C₂ – C₁t). (2.25)

Из (2.25) следует, что каждое оптимальное управление u*(t), 0  t  T, является кусочно-постоянной функцией, принимающей значения 1 и имеющей не более двух интервалов постоянства (ибо линейная функция C₂ – C₁t не более одного раза меняет знак на отрезке 0  t  T). Обратно, любая такая функция u(t) может быть получена из соотношения (2.25) при некоторых значениях постоянных C₁, C₂.

Наконец, переходим к третьему этапу: зная управление, найдем соответствующую траекторию системы.

Для отрезка времени, на котором u*  1, в силу системы (2.23) имеем:

,

Рис. 2.6. Семейства парабол для примера 2.2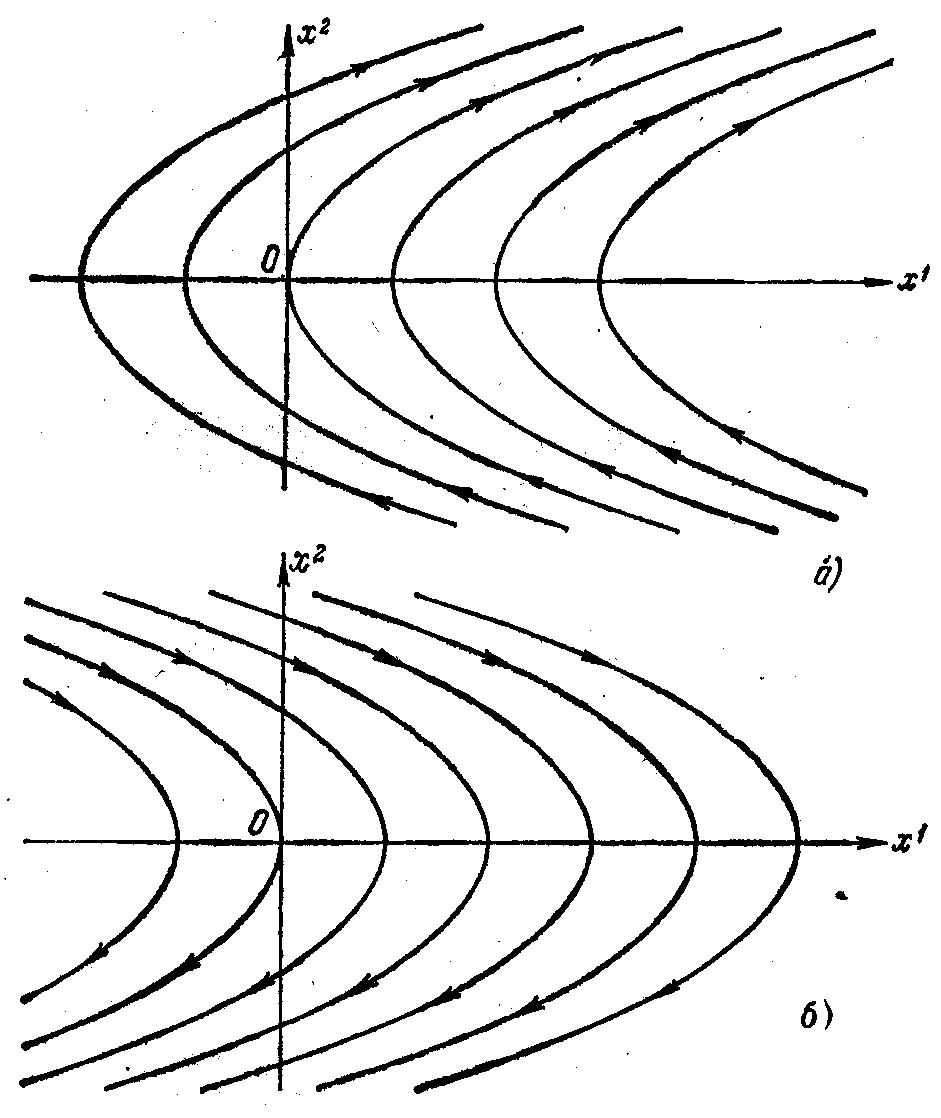

Рис. 2.7. Рисунки фазовых кривых

где S₁, S₂ – постоянные интегрирования. Отсюда получаем:

(2.26)

( – постоянная). Таким образом, кусок фазовой траектории, для которого u*  1, представляет собой дугу параболы (2.26). Семейство парабол (2.26) показано на рис. 2.6 а).

Аналогично, для отрезка времени, на котором u*  –1, мы имеем:

,

откуда получаем:

. (2.27)

Семейство парабол (2.27) показано на рис. 2.6 б). По параболам (2.26) фазовые точки движутся снизу вверх (ибо , т.е. – возрастающая функция параметра времени t, и движение должно происходить в сторону увеличения ), а по параболам (2.27) – сверху вниз ( , и движение должно происходить в сторону убывания ).

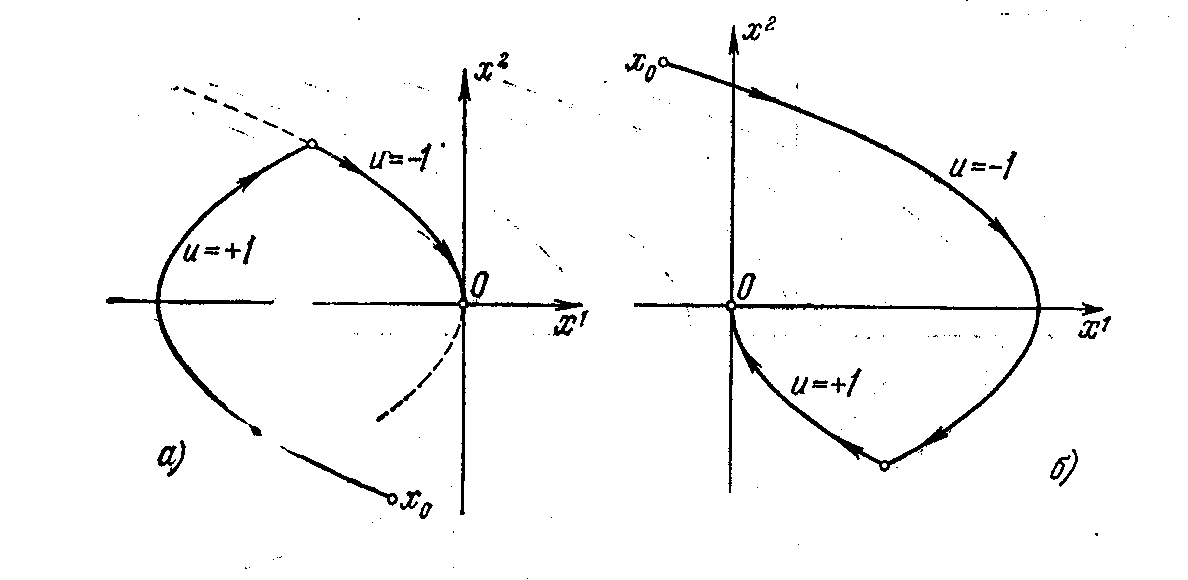
Рис. 2.7. Примеры фазовых траекторий

Как и было указано выше, каждое оптимальное управление является кусочно-постоянной функцией, принимающей значения 1 и имеющей не более двух интервалов постоянства. Если управление сначала, в течение некоторого времени, равно +1, а затем равно –1, то фазовая траектория состоит из двух кусков парабол (рис. 2.7 а)), примыкающих друг к другу, причем первый из этих кусков принадлежит параболе из семейства (2.26), а второй лежит на той из парабол (2.27), которая проходит через начало координат (ибо искомая траектория должна вести в начало координат). Если же, наоборот, сначала u* = –1, а затем u* = +1, то вначале движение идет вдоль кривой семейства (2.27), а затем – вдоль параболы (2.26), проходящей через начало координат (рис. 2.7 б)). На дугах парабол на рис. 2.7 надписаны соответствующие значения управляющего параметра u.

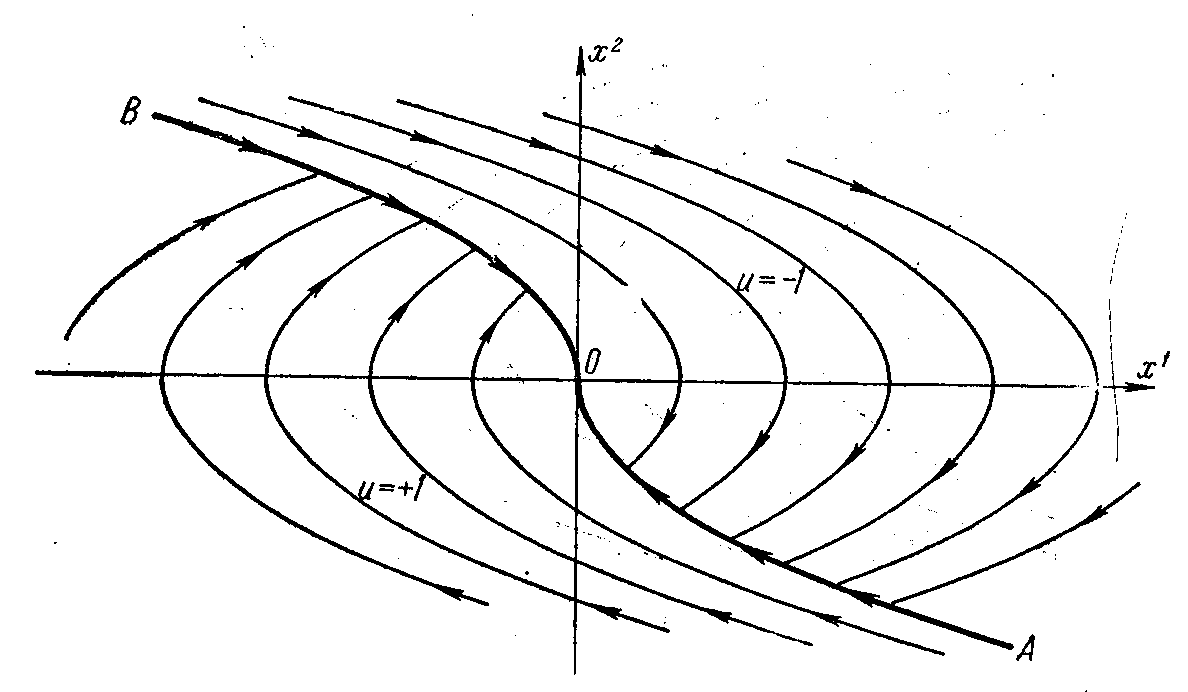
Рис. 2.8. Семейство фазовых траекторий

На рис. 2.8 изображено все семейство полученных таким образом фазовых траекторий (АО – дуга параболы , расположенная в нижней полуплоскости, ВО – дуга параболы , расположенная в верхней полуплоскости, только эти кривые приводят фазовую точку в начало координат).

Если начальная точка x⁰ расположена выше линии АОВ, то парабола (2.26) уводит фазовую точку от начала координат, поэтому двигаться нужно по дуге параболы (2.27) под воздействием управления u = –1 до тех пор, пока точка не попадет на дугу АО. В момент попадания на дугу АО значение u переключается и становится равным +1 вплоть до момента попадания в начало координат. Аналогичным образом, если начальное положение x⁰ расположено ниже линии АОВ, то фазовая точка должна двигаться по дуге параболы (2.26) до момента попадания на дугу ВО (при этом значение u равно +1), а в момент попадания на дугу ВО значение u переключается и становится равным –1. Наконец, если начальное положение x⁰ оказывается на линии АОВ, то переход в начало координат не требует переключения управления, и для дуги AO оно равняется +1, а для дуги BO управление равно –1. Отметим, что кривую АОВ называют линией переключений (см. также §6).

Итак, с помощью принципа максимума мы получили, что из каждой точки фазовой плоскости исходит только одна экстремальная траектория, ведущая в начало координат (т.е. задание начальной точки x⁰ однозначно определяет соответствующую траекторию). Более того, поскольку для автономных линейных задач на быстродействие принцип максимума Понтрягина является необходимым и достаточным условием оптимальности, то найденные траектории (рис. 2.8) являются оптимальными, и других оптимальных траекторий, ведущих в начало координат, не существует.

Пример 2.3. Рассмотрим для точки, движущейся по рассмотренному в предыдущем примере закону (2.23) (с тем же ограничением ), задачу о быстрейшем попадании на ось x₂ из заданного начального состояния x⁰. В этом случае мы имеем задачу с подвижным правым концом, где терминальным множеством М¹ служит прямая x₁ = 0.

Поскольку граничное условие для вектора x на правом конце отсутствует, то вместо него ставится так называемое условие трансверсальности на вектор , заключающееся в ортогональности этого вектора к опорной гиперплоскости множества М¹ в точке x(T). Подробнее о подобных задачах см. раздел 3.

Чтобы выписать условие трансверсальности для рассматриваемой задачи, найдем вектор  = ( ₁,  ₂), касающийся множества М¹ (в произвольной точке). В данном случае он имеет вид  = (0,  ₂), где  ₂  0. Следовательно, условие трансверсальности в правом конце записывается в форме , откуда .

Используем результаты примера 2.2. Так как функция ₂ линейна, то из соотношения вытекает, что ₂(t) сохраняет постоянный знак при 0  t < T. Таким образом (см. (2.25)), в этом случае каждое оптимальное управление постоянно и равно +1 или –1, и потому оптимальными могут быть только движения по параболам (2.26), (2.27) (без переключений).

Изучим множество 0-управляемости.

Предположим сначала, что начальное фазовое состояние x₀ находится справа от прямой x₁ = 0. Согласно сказанному выше, через точку x⁰ проходят только две фазовые траектории, которые могут оказаться оптимальными: траектория (2.26), по которой движение происходит снизу вверх, и траектория (2.27), по которой движение происходит сверху вниз (рис. 2.9).

Если точка x₀ расположена выше линии АО (см. рис. 2.8), то, двигаясь по параболе (2.26), фазовая точка не попадет на ось x₁ = 0 (рис. 2.10), и потому оптимальным может быть только движение по параболе (2.27).

Если же точка x⁰ расположена на линии АО или ниже нее, то оба движения (2.26), (2.27) приводят фазовую точку на ось x₁ = 0 (рис. 2.11). Итак, в этом случае имеются две траектории, удовлетворяющие принципу максимума.

Однако легко видеть, что время движения по этим траекториям из точки x⁰ до оси x₁ = 0 различно. Действительно, проведя касательные к параболам (2.26) и (2.27) в точке x⁰, мы легко найдем (см. рис. 2.12), что Q₀Q₂ > Q₀P₂ = Q₀P₁ > Q₀Q₁, а так как при u =  время движения по дуге параболы равно разности ординат (см. второе уравнение (2.23)), то движение по дуге x⁰Q₂ происходит дольше, чем по дуге x⁰Q₁. Таким образом, и в этом случае оптимальным может быть только движение по траектории (2.27). Итак, в правой полуплоскости оптимальными могут быть только движения по параболам (2.27), т.е. движения, совершающиеся при u = –1.

Аналогично, слева от оси x₁ = 0 оптимальными могут быть только движения по параболам (2.26), т.е. движения, совершающиеся при u = +1.

Это и дает функцию оптимального управления:

.

Фазовая картина оптимальных траекторий изображена на рис. 2.13.

Пример 2.4. Рассмотрим систему с законом движения

(2.28)

Пусть даны: ограничение на управление , начальное состояние x₁(0) = –1, x₂(0) = 1 в момент времени t = 0, целевой функционал

,

где T = 2 известно.

Поставленная задача – это задача с фиксированным временем и свободным правым концом, функционал в этой задаче смешанный. Преобразуем функционал в интегральный:

.

Третье слагаемое в подынтегральной функции можно заменить, используя закон движения:

.

С учетом краевых условий и заданного конечного времени T = 2 приходим к следующему виду целевого функционала:

.

Появившееся постоянное слагаемое 1 никак не влияет на выбор оптимального решения и его можно отбросить, заменив исходный функционал другим:

.

Применим к данной задаче принцип максимума. Поскольку вместо задачи оптимального быстродействия имеем задачу Лагранжа более общего вида, то для ее решения понадобится функция Понтрягина (см. раздел 3):

.

Эта функция является линейной по управлению u и поэтому достигает максимального значения либо при , либо при u = 1 в зависимости от знака выражения , т.е.

.

Запишем сопряженную систему:

.

Общее решение системы имеет вид

а учитывая краевые условия , для сопряженных переменных на правом конце, находим C₁ = 0, C₂ = –1, C₃ = –1, т.е.

.

Итак, , и мы можем записать экстремальное управление, анализируя знаки функции –1– 2 cost:

Поскольку найдено лишь одно управление, удовлетворяющее принципу максимума, оно и будет оптимальным при условии, что оптимальное управление в данной задаче существует. Определим экстремальную траекторию, соответствующую найденному управлению. Для этого необходимо решить систему (2.28) при двух возможных значениях u. На промежутке при имеем систему

(2.29)

решая которую, получим:

. (2.30)

Из начальных условий x₁(0) = –1, x₂(0) = 1 определяем постоянные интегрирования C₁ и C₂. С учетом этих постоянных имеем

. (2.31)

Очевидно, что при движении по найденной траектории в момент времени фазовая точка будет находиться в состоянии

.

На промежутке экстремальная траектория определяется системой

Общее решение этой системы имеет вид

.

Подставляя в общее решение найденные значения , при , получим систему относительно неизвестных постоянных:

.

Решая эту систему, находим . Следовательно, на промежутке экстремальной будет траектория

. (2.32)

На промежутке экстремальная траектория удовлетворяет той же системе (2.29), что и на первом участке, и, следовательно, имеет вид (2.30). Согласно (2.32), при имеем

.

Как и выше, составляем систему относительно неизвестных постоянных C₁ и C₂:

.

Решая ее, находим: . Таким образом, последний участок искомой траектории описывается системой

. (2.33)

Из соотношений (2.31), (2.32), (2.33) следует, что экстремальная траектория состоит из дуг трех окружностей (рис. 2.14).

Н а первом участке экстремальная фазовая траектория описывается уравнением , на втором участке – уравнением , на третьем участке – уравнением . Движение по дугам фазовой кривой осуществляется согласно направлению вектора фазовой скорости, т.е. по часовой стрелке.

Задачи

1. Решить следующие задачи оптимального быстродействия:

1. 

2. 

3. 

4. 

2. Решить задачу оптимального быстродействия с подвижным правым концом:

3. Решить задачи оптимального управления с фиксированным временем:

1. 

2. 

4. Найти оптимальное управление и оптимальную траекторию в следующих задачах оптимального управления:

1. 

2. 

5. При условиях минимизировать следующие функционалы:

1) 2)