- •Раздел 2. Линейные задачи оптимального управления
- •Раздел 2. Линейные задачи оптимального управления
- •§1. Постановка задачи
- •§2. Области достижимости и управляемости
- •§3. Существование оптимальных управлений
- •§4. Экстремальные управления
- •§5. Принцип максимума для линейных задач оптимального управления
- •§6. Структура оптимального управления
- •§7. Вычисление оптимального управления
- •§8. Примеры решения линейных задач оптимального управления с применением принципа максимума
- •Вопросы для самопроверки
§3. Существование оптимальных управлений
В вопросе существования оптимального управления важную роль играет ограниченность множества U. Покажем это на примере.
Пример
2.1. Рассмотрим
задачу на быстродействие в
![]() с одним управляющим параметром:
с одним управляющим параметром:
![]()
x(0) = x0, x(T) = 0;
T min.
Рассмотрим два случая относительно множества U.
U R1 (т.е. U – неограниченное множество).
Для произвольного числа T > 0 построим функцию :
![]()
Очевидно, для любого t u(t)U, т.е. является допустимым управлением, причем это есть непрерывная на [0,T] функция.
Подставляя это управление в уравнение движения и применяя формулу (2.8), вычислим соответствующую траекторию :
![]()
Видно,
что при
t = T
x(T) = 0
при любом начальном состоянии
x0,
т.е.
![]() решает задачу управления (приводит
систему в начало координат за некоторое
время T).
С другой стороны, какое бы малое число
T > 0
мы ни взяли, управление
остается допустимым, а траектория
к этому моменту приходит в начало
координат. Таким образом, оптимального
управления не существует (против любого
управления, приводящего систему в начало
координат, можно найти еще лучшее в
смысле минимизации времени T).
Здесь
G R1.
решает задачу управления (приводит
систему в начало координат за некоторое
время T).
С другой стороны, какое бы малое число
T > 0
мы ни взяли, управление
остается допустимым, а траектория
к этому моменту приходит в начало
координат. Таким образом, оптимального
управления не существует (против любого
управления, приводящего систему в начало
координат, можно найти еще лучшее в
смысле минимизации времени T).
Здесь
G R1.
U = [–1,1] (т.е. U – ограниченное множество).
Для любого
допустимого управления
такого, что
![]() ,
и произвольного
T > 0,
применяя формулу (2.10),
имеем:
,
и произвольного
T > 0,
применяя формулу (2.10),
имеем:
![]()
![]()
Справедлива оценка:
![]()
Следовательно,
равенство (2.10) справедливо только для
тех начальных состояний
x0,
для которых
![]() .
В этом случае область 0-управляемости
есть
.
В этом случае область 0-управляемости
есть
![]() .
После изучения методов вычисления можно
убедиться, что в этой области задача
быстрейшего попадания в начало координат
имеет единственное решение
.
После изучения методов вычисления можно
убедиться, что в этой области задача
быстрейшего попадания в начало координат
имеет единственное решение
![]() (задача управления имеет бесконечное
множество решений).
(задача управления имеет бесконечное
множество решений).
В терминах области управляемости в автономной задаче на быстродействие справедлива следующая теорема существования.
Теорема 2.4.
Пусть в задаче на быстродействие в
автономной системе (2.7) множество U
компактно в
![]() .
Тогда для любой точки
.
Тогда для любой точки
![]() существует, и притом единственное,
оптимальное управление.
существует, и притом единственное,
оптимальное управление.
Следующее утверждение является следствием теорем 2.3 и 2.4.
Следствие.
Пусть в автономной системе (2.7) U
компактно в
,
![]() ,
матрица A
устойчива (или выполнено условие общности
положения (2.9)). Тогда для любого
,
матрица A
устойчива (или выполнено условие общности
положения (2.9)). Тогда для любого
![]() существует единственное оптимальное
по быстродействию в начало координат
управление.
существует единственное оптимальное
по быстродействию в начало координат
управление.
Докажем более общую теорему существования для неавтономной системы.
Теорема 2.5. Пусть в неавтономной линейной задаче оптимального управления (2.1)-(2.5) выполнены следующие условия:
множество U компактно в Rm;
целевое множество M(t) компактно и непрерывно меняется на [0,T];
задача управления разрешима, т.е. существует управление , переводящее систему из состояния x0 в M(T).
Тогда в задаче
(2.1)-(2.5) существует оптимальное по
быстродействию (измеримое) управление
![]() :
:
![]() ,
,
![]()
Доказательство.
Случай
![]() является тривиальным, т.е. в этом случае
является тривиальным, т.е. в этом случае
![]() .
Поэтому предполагаем
.
Поэтому предполагаем
![]() .
Обозначим
.
Обозначим
![]() .
.
В
силу непрерывности M(t)
и K(t)
(см. теорему 2.1) и разрешимости задачи
управления момент T*
существует. По определению это есть
минимальное время достижения целевого
множества M(t)
из начальной точки
![]() .
Заметим, что либо такой момент единственен,
если множества K(t)
и M(t)
строго выпуклы, либо их множество
замкнуто в Rn.
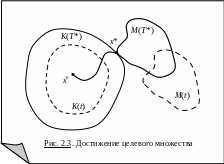
Точку касания множеств K(T*)
и M(T*)
обозначим x*
(см. рис.
2.3). По определению множества достижимости
K(T*)
существует допустимая траектория
.
Заметим, что либо такой момент единственен,
если множества K(t)
и M(t)
строго выпуклы, либо их множество
замкнуто в Rn.
Точку касания множеств K(T*)
и M(T*)
обозначим x*
(см. рис.
2.3). По определению множества достижимости
K(T*)
существует допустимая траектория
![]() такая, что
такая, что
![]() .
Порождающее эту траекторию допустимое
управление
и является оптимальным по быстродействию,
ибо оно приводит систему в целевое
множество за минимальное время
Теорема доказана.
.
Порождающее эту траекторию допустимое
управление
и является оптимальным по быстродействию,
ибо оно приводит систему в целевое
множество за минимальное время
Теорема доказана.