Оптимизация сапр Лекция №1 Постановка задачи оптимизации
М
одель
оптимизируемого объекта.
1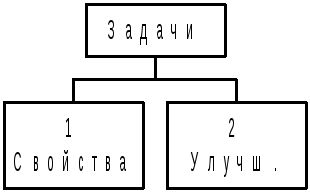
)
Анализ модели:
определ. вект. вых. хар-к.
2) Изменение модели: → структурные: кол-во переменных, кас. Ф (измен.)
→ параметрические: изм. пар-ров
–обычно
фиксирован.
В
обычно выделяют: подмножество коэф.
наз-ся вектор варьируемого коэф.
Будем
считать, что
.
Обычно на значения коэф.
накладываются ограничения, определ.
услов. их физ. реализуемости.
Скорее
всего в этой последовательности
наилучший вариант.
Задача.
Найти такое значение
обеспеч. наилучшие вых. хар-ки (чаще
всего встреч.)
Свойства модели (влияющие на нахождение наилучш. вых. хар-ки.):
Аналит. зависимость, анал. выр. исп. теорет. зн. < 1%
Алгорит.
завис-ть, вычисл. задача (система ур-й),
99%
Дискрет. или непрерыв. хар-р зависимость вых. хар-к от варьир. параметров.
Если хар-р зав. непр., то ф-ии бывают гладкие или нет (это можно оценить) и порядок гладкости.
Наклад. ограничения на вар. парам. или нет? Можно ли их классифицировать, если есть?
Трудоемкость процесса анализа, вычисл. производных.
Эти свойства модели очень важны.
Пример:
Смысл
ур-й менять нельзя, но можно менять
коэффициент.
Будем рассматривать параметр. изменения.
Постановка задач оптимизации.
Дано:
Мат. модель.
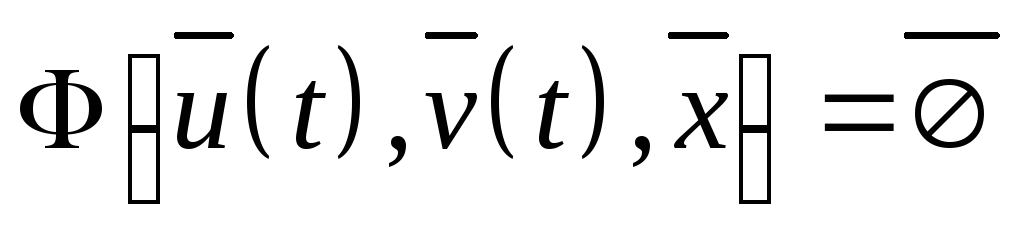
D – это ограничение на
,
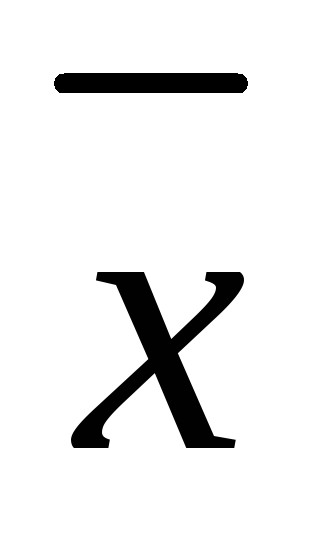вытекающее из специфики решения задачи.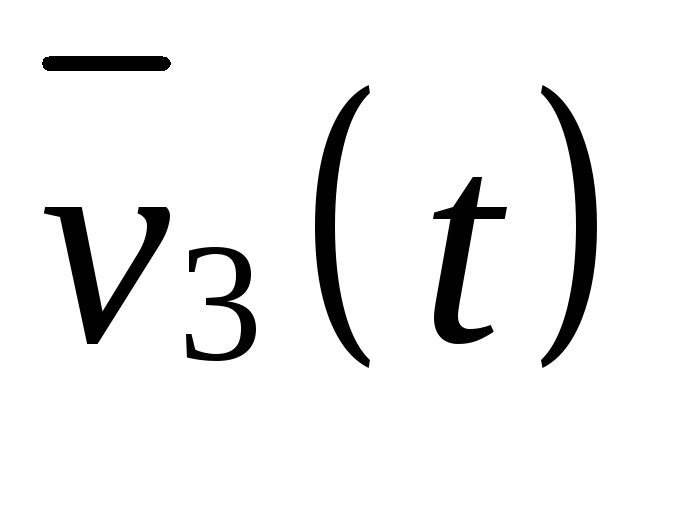
-
то, к чему должны стремиться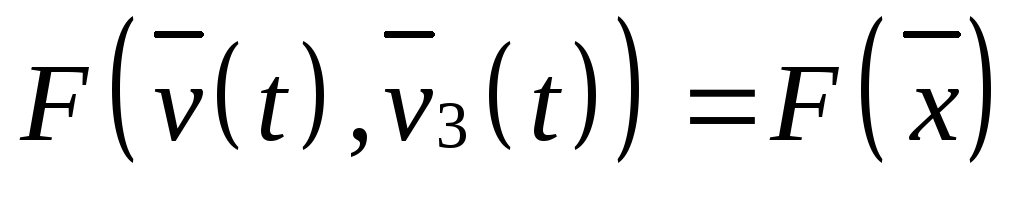
-
целевая функция, критерий качества,
функционал качества (разница между
желаемым и действительным).
Замечание. Построению F будет посвящена отдельная тема.
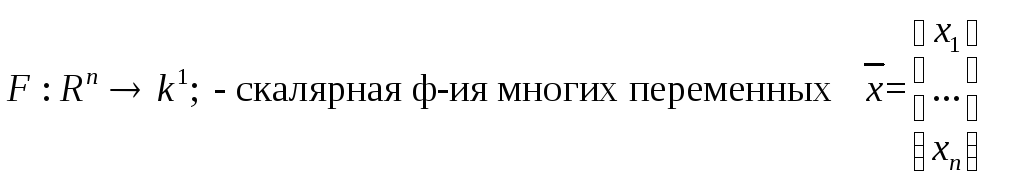
Функционал отображает вектор в скаляр.
Не всегда функционал отображает разницу между жел. и действит., но иногда и занимается поиском max и min и т.д.
Смысл F:
А) «как можно больше» (обратная задача)
Б) «как можно меньше»
В) «как можно ближе» (min разности между желаемым и действительным)
Во всех трех случаях речь идет о поиске min.
Найти:
Обсуждение основных подходов к решению задач.
Аналитический – исп. ан. мет. для поиска min значений. Недостаток: треб. аналит. зав. (1%), которая чаще всего отсутствует., треб. высокая квалификация человека, задачи могут оказаться очень сложными.
С
канирование
Если сотни параметров, то этот подход не подходит.
Поисковые методы оптимизации
Нас
интересует время решения этой задачи
Нам нужно уменьшить Т.
Типовой алгоритм:
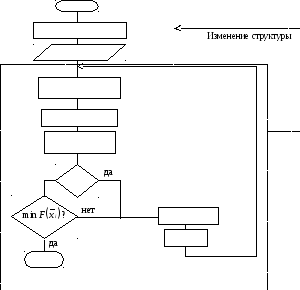Начало
Синтез структ. мод.
Задание N, i=0
Анализ мод.
Вычисл.
конец
Задача математического программирования
Если целевая функция или ограничения не линейны, то это задача нелинейного математического программирования.
Если целевая функция или ограничения линейны, то это задача линейного математического программирования.
В течение ближайших 6 тем не обращаем внимания на F.
В зависимости от вида целевой функции и ограничений задачу можно классифицировать.
Если ограничения заданы, то задача условной оптимизации, иначе безусловной оптимизации.
