Министерство образования и науки Российской Федерации

ФГБОУ ВПО

Всероссийский заочный финансово-экономический институт

Курсовая работа

По дисциплине «Информатика»

На тему: «Системы счисления в компьютерной обработке информации»

Вариант № 7

Исполнитель: Попова Марина Александровна

Факультет: непрерывного обучения

Направление подготовки: менеджмент

Группа: день, базовый уровень

№ личного дела: 11МЛД12152

Проверил: Комарцова Людмила Георгевна

Калуга – 2011

Содержание

Введение………………………………………………………………………..3

1. Теоретическая часть ……………………………………………………...4

1.1. Системы счисления……………………………………………………….4

1.2. Арифметические операции над числами, представленными в различных системах счисления……………………………………………………8

1.3. Представление чисел в компьютере……………………………………..9

2. Практическая часть……………………………………………………...15

2.1. Постановка задачи……………………………………………………..15

2.1.1. Цель решения задачи ………………………………………………….15

2.1.2. Условие задачи ………………………………………………………..15

2.2. Компьютерная модель решения задачи …………………………….17

2.2.1. Информационная модель решения задачи …………………………..17

2.2.2. Аналитическая модель решения задачи ……………………………..17

2.2.3.Технология решения задачи …………………………………………..18

2.3. Результаты компьютерного эксперимента и их анализ ………….23

2.3.1. Результаты компьютерного эксперимента …………………………..23

2.3.2. Анализ полученных результатов……………………………………..25

Заключение……………………………………………………………………26

Список использованной литературы………………………………………..27

Введение

Каждый регистр арифметического устройства ЭВМ, каждая ячейка памяти представляет собой физическую систему, состоящую из некоторого числа однородных элементов. Каждый такой элемент способен находиться в нескольких состояниях и служит для изображения одного из разрядов числа. Именно поэтому каждый элемент ячейки называют разрядом. Нумерацию разрядов в ячейке принято вести справа налево, самый левый разряд имеет порядковый номер 0. Наиболее надежным и дешевым является устройство, каждый разряд которого может принимать два состояния: намагничено - не намагничено, высокое напряжение - низкое напряжение и т.д. В современной электронике развитие аппаратной базы ЭВМ идет именно в этом направлении.

1. Теоретическая часть

1.1. Системы счисления

Для записи информации о количестве объектов материального мира используются числа, которые разделяются по определенным признакам. На рис. 1 представлена классификация чисел по групповому признаку, когда в каждую группу входят числа, обладающие определенными свойствами.

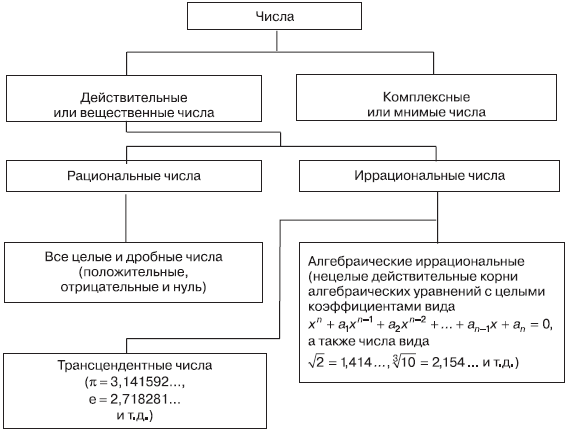
Рис. 1. Классификация чисел

Числа записываются с использованием особых знаковых систем, которые называются системами счисления, в них числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами.

Все системы счисления делятся на два вида: позиционные и непозиционные. В позиционных системах счисления значение цифры зависит от ее положения в числе, в непозиционных – не зависит. Самой распространенной из непозиционных систем является римская. В качестве цифр в римской системе используются следующие символы: I (1), V (5), X (10), L (50), С (100), D (500), М (1000). Значение цифры в этой системе не зависит от ее положения в числе. Величина числа в римской системе определяется как сумма и разность цифр в числе. Если меньшая цифра стоит слева от большей, то она вычитается, если справа – прибавляется.

Например, число 1997 (десятичная позиционная система счисления) в римской системе счисления будет выглядеть следующим образом: MCMXCVII = 1000 + (1000 – 100) + (100 – 10) + 5 + 1 + 1.

Наибольшее применение при вводе, обработке и выводе информации в компьютере и компьютерных системах нашли позиционные системы счисления, при этом самыми распространенными являются десятичная, двоичная, восьмеричная и шестнадцатеричная системы. В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе. Основание системы равно количеству цифр (знаков ее алфавита) и определяет, во сколько раз различаются значения цифр соседних разрядов числа. В общем случае в позиционной системе счисления любое число, содержащее целую и дробные части, в развернутой форме может быть представлено в виде:

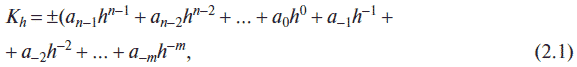
или в рекуррентной форме:

где K – представляемое число; h – основание системы счисления; а – разрядный коэффициент, а = 0, 1, 2, 3…, h-1, т. е. цифры, принадлежащие алфавиту данной системы счисления; i – номер разряда, позиция; n – число целых разрядов числа; m – число дробных разрядов числа.

В десятичной системе счисления формула (2.2) может быть записана следующим образом:

где а = 0, 1, 2, 3…, 9.

Например, число 827 десятичной системы счисления в соответствии с выражением (2.3) можно представить в виде: 827 = 8 · 102 + 2 · 101 + 7 · 100.

Десятичная система исчисления используется в компьютерах для ввода числовых данных и отображения полученного результата. Все внутренние, промежуточные операции компьютер производит в двоичной системе счисления и соотношение (2.2) примет вид:

где а = 0, 1.

Например, число 11001110112 двоичной системы счисления в соответствии с формулой (2.4) можно представить в виде: 1 · 29 + 1 · 28 + 0 · 27 + 0 · 26 + 1 · 25 + 1 · 24 + 1 · 23 + 0 · 22 + 1 · 21 + 1 · 20.

Достаточно широко при компьютерной обработке информации применяются восьмеричная и шестнадцатеричная системы счисления, которые используются, например, для обозначения адресов расположения данных в памяти компьютера и т. д.

Соотношение (2.2) для восьмеричной и шестнадцатеричной системы счисления соответственно примет вид (2.5) и (2.6) :

где а = 0, 1, 2, 3…, 7.

Например, число 14738 восьмеричной системы счисления в соответствии с (2.5) примет вид: 1 · 83 + 4 · 82 + 7 · 81 + 3 · 80.

где а = 0, 1, 2, 3…, 9, A, B, C, D, E, F.

В шестнадцатеричной системе счисления используется шестнадцать цифр, из которых десять цифр арабские (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), а остальные цифры (10, 11, 12, 13, 14, 15) обозначаются буквами латинского алфавита (А = 10, В = 11, С = 12, D = 13, E = 14, F = 15).

Например, число 33B16 шестнадцатеричной системы счисления, в соответствии с (2.6) примет вид: 3 · 162 + 3 · 161 + В · 160 (В = 11).

При операциях с числами, представленными в различных системах счисления, необходимо указывать систему счисления числа, используя нижний индекс, например: 82710 – число 827 в десятичной системе; 11001110112 – число 1100111011 в двоичной системе; 14738 – число 1473 в восьмеричной системе; 33B16 – число 33В в шестнадцатеричной системе счисления.

Преобразование чисел, представленных в двоичной, восьмеричной и шестнадцатеричной системах счисления, в десятичную осуществляется достаточно просто. Для этого необходимо записать число в развернутой форме в соответствии с выражением (2.1) и вычислить его значение. Например:

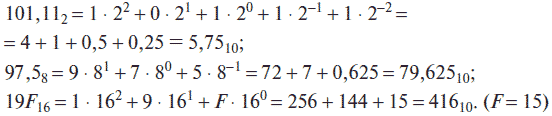
Преобразование чисел, представленных в десятичной системе счисления, в двоичную, восьмеричную и шестнадцатеричную системы счисления – более сложная процедура, которая может осуществляться различными способами: деления, умножения, вычитания и т. д. При этом необходимо учитывать, что способы перевода целых десятичных чисел и правильных дробей будут различаться. Для перевода целого десятичного числа, например 5310, в двоичную систему можно использовать способ деления, а десятичной правильной дроби, например 0,7510, в двоичную систему – способ умножения. Результаты действий отобразим в соответствующих табл. 1 и 2.

Таблица 1

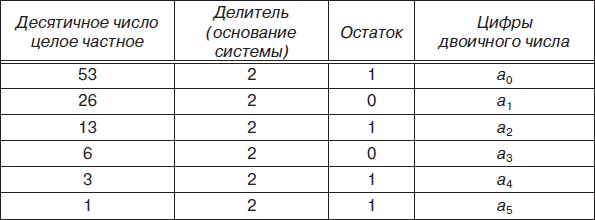
Таким образом, 5310 = 1101012.

Таблица 2

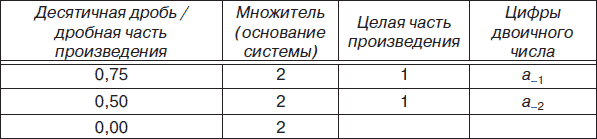
Таким образом, 0,7510 = 0,112.