Системное моделирование организации

Моделирование - метод исследования объектов, посредством представления их на моделях реально существующих предметов.

Модель - мера, норма, образец, аналог определенного фрагмента, оригинала объекта.

Для исследования объекта моделируем не весь объект, а его часть посредством абстрагирования от других частей.

По характеру модели различают:

1) предметные - воспроизводящие физические, геометрические и другие аналогичные характеристики объекта оригинала.

2) знаковые - схемы, чертежи, рисунки.

При моделировании объекта различают:

- модель структуры объекта;

- модель процесса объекта;

- модель функционирования объекта, что отражает поведение объекта

Модель - логико-вербальное или математическое описание объекта оригинала, отражающее интересующее нас свойство объекта.

Модель и оригинал одинаковы по своим целям.

Различают статистические и динамические модели.

Статистическая модель - отражает конкретное состояние объекта оригинала в какой-то отрезок времени.

Динамическая модель - отражает процесс изменения состояния оригинала, т.е. функциональная модель.

По способу воплощения модели бывают:

- абстрактные

- материальные

Абстрактная (виртуальная) модель - есть идеальная конструкция, построенная в воображении человека.

Материальная модель - вещественно-реальные модели, являющиеся отражением оригинала, представляющие собой материальные конструкции с установленным отношением подобия адекватности оригинала.

Существует:

1) прямое подобие, как результат взаимодействия оригинала и объекта (макет, фото);

2) косвенно установленное подобие между объектом и моделью без физического взаимодействия, но объективно существует в природе.

Абстрактность модели - это невозможность конечного определения, невозможность материализации в том виде, в котором она сформирована в сознании - только косвенное понятие (например, автопилот).

3) условное подобие (например, деньги-модель стоимости)

Условное подобие устанавливается в рамках какого-то соглашения.

Требования к моделям:

1. упрощенность модели.

Модель должна быть конечна, ограниченна, т.к. любой оригинал бесконечен. Модель всегда проще оригинала, т.к. выделяется только конкретные объекты, фрагменты для моделирования.

2. приближенность модели.

Модель есть приблизительное отражение оригинала и никогда не будет равна оригиналу, но всегда будет к этому приближаться.

3. адекватность модели поставленной цели.

Определяет необходимость выполнения требований, соответствия и достаточности модели для достижения цели исследуемого объекта.

4. истинность модели.

Использование в моделировании норм, законов, процессов функционирования объекта оригинала, посредством которых достигается достоверность результатов моделирования и возможность переносов результатов на исследуемый объект.

5. входные параметры и их размерности должны быть согласованны с выходными параметрами и их размерностями.

Точность выходных параметров не должна превышать точность входных.

Процесс моделирования

Рассмотрим простейшую модель «вход-выход»:

r

m₂

m₁

X Y

m_n

М = {m₁, m₂, … m_n} элементы соединены связью.

R {r₁₂ r₂₂ r… r_mn}

x {x₁, x₂, … x_n}  (x₁, x₂, … x_n)

Y { Y₁, Y₂, … Y_m} (y₁, y₂, … y_m)  (y₁, y₂, y₃, y₄)

R { m₁*m₂*…*m_n}

R {r₁ r … r_mn}

R {X C Y}  {Y₁ X₁… Y_mX_n}

пересечение параметру входа

входа и выхода; соответствует параметр выхода.

Простейшая модель «вход-выход» сформулирована как модель элементов, представляющих множество М, которые по средством имеющихся внутренних связей между элементами r определяют процесс функционирования системы.

В итоге существующих взаимосвязей определяют входы и выходы каждого элемента m в качестве совокупного входа Х и выхода У.

Совокупный вход Х представляет собой множество переменных х₁ … x_n, имеющих свои численные значения (х₁ … x_n).

Совокупный выход У представляет собой множество переменных Y₁, Y₂, … Y_m, имеющих свои координаты (y₁, y₂, … y_m).

Множество элементов М образуют отношения между входом Х и выходом У, которые обозначаются R.

Пусть множество R определяет декартовое произведение элементов системы между входом Х и выходом У, что в итоге сводится к отношению входа и выхода, задаваемое переменными входа и выхода. Т.к. R (m₁*m₂*…*m_n), тосвязи между ними можно представить в виде множества раскрывающего отношение входа и выхода.

Заменим произведение элементов на их связи:

R {X * Y}  {Y₁ * X₁ … Y_m * X_n}

Т.о. R {X * Y} (R есть отношение X на Y)

Каждому элементу входа соответствует элемент выхода (переменная - элемент).

Появляются пары элементов (x_i y_i).

Т.о. система определяется как соответствие подмножества X и Y, образуемые в результате декартового произведения входа на выход в виде множества, содержащего упорядоченные пары.

XY = {X₁Y₁ … X_iY_j}

Т.о. вход (Х), задаваемый своими числовыми значениями, физически представленных в виде каких-либо ресурсов, которые трансформируются в системе по средством внутренних свойств и взаимосвязей, которые в совокупности определяются отношением R в параметры функционирования системы Y, которая выводится во внешнею среду в множестве переменных.

Множество Y определяет результаты работы системы по средством трансформации Х через множества отношения R.

Т.о. модель системы «вход-выход» можно описать следующими отношениями Х, Y и R.

S = < Х, Y, R >

Отношение R в картеже выступает как функция изменения выходного сигнала в зависимости РТ входного и является отображением функции Х на Y.

Х  R (Y)

Когда модель R выступает в виде функции (RF), то можно представить выход как взаимосвязь Y= F*Х; Y=f (х).

Вывод: данная модель справедлива для статических моделей, когда имеет место 1-а соответствие (1-а, степень свободы), изменяется по закону линейному и каждому входу Х соответствует единичный параметр Y.

В природе таких объектов не бывает.

Рассмотрим объект, в котором Z ≠ 1.

Система имеет состояние Z, все остальное справедливо.

.

.

Z

R₁ R₂

m₁ m₂

.

m_n S

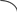
X Y

Z {Z₁ Z₂ Z₃ … Z_n}

Состояние Z определяет свойство элементов в момент, зависящий от времени или от подаваемого сигнала Х.

Т.о. состояние Z как множества {Z₁ … Z_n} формируется как отражение действия внешних и внутренних факторов.

В рассматриваемый момент времени t каждая такая система имеет состояние Z, которое в момент t зависит от входа Х (состояния) и предшествующего состояния Z’ в момент времени t-1.

Т.о. можно определить отражение входа Х и предшествующего состояния Z’ на текущее состояние системы Z и определить отношение R₁, как отношение входа Х и текущего состояния Z.

(Х Z’) * R_{1 *} Z_s = (Х Z’_t-1) * R₁ * Z_t

Параметры выхода системы Y в этом случае определяется как отношение текущего состояния Z к выходу по средством отношения R₂.

Z_t * R₂ * Y

Y: надо убрать из входа Z и R₁.

Т.о. после проведения вычислений система описывается следующим картежом:

S <X Y Z_t R₁ R₂>

S_t<X Y Z_t R₁ R₂ T>

F₁ F₂

В случае динамичности системы в картеже появляется параметр времени t.

Произведение t на состояние системы дает такое множество, которое называется пространством событий, в котором наблюдаются такие единичные пары t* Z, являющиеся свершением событий функции F.

(t_j* Z_i)  F_i

В этом случае отношение R₁ определяет траекторию развития системы в пространстве, а R₂ представляет состояние системы как функцию его отношения к выходу Y.