2. Матричный способ представления

Это - частный способ табличного представления логических функций. В частности – карты Карно.

Изобретены в 1952 Эдвардом В. Вейчем (диаграммы Вейча) и усовершенствованы в 1953 Морисом Карно (карты Карно).

Таблица 1.2 – Карта Карно четырех переменных

х3х4 х1х2	00	01	11	10
00	0	1	1	0
01	1	0	0	0
11	0	0	1	0
10	1	0	1	0

3. Графический способ представления

Логическая функция n переменных представляется n – мерным кубом, где каждый двоичный набор это n – мерный вектор, определяющий точку n – мерного пространства.

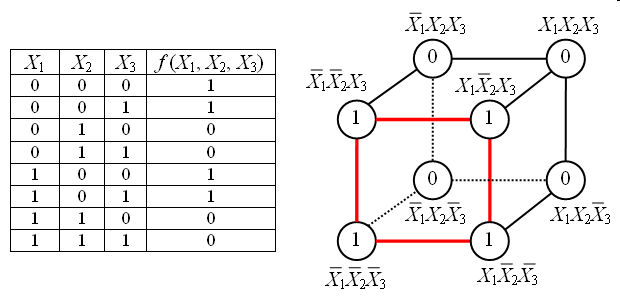
Рисунок 1.1 – Графическое представление функции трех переменных

4. Аналитический способ представления

Для этого вводится множество функций, а также правила зависимости функций от набора переменных, т.е. формулы – аналитические выражения на основе операций булевой алгебры.

1.4Логические функции

1. Логические функции одной переменной

Количество логических функций в зависимости от числа переменных определяется следующим соотношением:

_n

2 ² , т.к. функция и n аргументов принимают по 2 значения, т.е.

для одной переменной будет 4 функции:

Таблица 1.3 – Функции одной переменной

х	F0	F1	F2	F3
0	0	0	1	1
1	0	1	0	1

F₀ (х) = 0 - константа нуля;

F₁ (х) = х - тождественная функция;

F₂ (х) = х – инверсия (отрицание);

F₃ (х) = 1 - константа единицы.

2. Логические функции двух переменных

Таблица 1.4 – Функции двух переменных

х1	х2	F0	F1	F2	F3	F4	F5	F6	F7	F8	F9	F10	F11	F12	F13	F14	F15
0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	0	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
обознач.		0		х1х2	х1	х2х1	х2					 х2	х2х1	 х1	х1х2		1

Наименования:

F₀ = 0 – константа нуля;

F₁ = х₁  х₂ конъюнкция (логическое умножение), может обозначаться

х₁ х₂;

F₂ = х₁  х₂ отрицание импликации (следования), может обозначаться

х₁  х₂;

F₃ = х₁ тождественная функция первой переменной;

F₄ = х₂  х₁ – отрицание обратной импликации;

F₅ = х₂ тождественная функция второй переменной;;

F₆ = х₁  х₂ – сложение по модулю 2 (неравнозначность);

F₇ = х₁  х₂ – дизъюнкция (логическое сложение);

F₈ = х₁  х₂ – стрелка Пирса;

F₉ = х₁  х₂ – эквиваленция, может обозначаться х₁  х₂, х₁  х₂;

F₁₀ =  х₂ – отрицание (инверсия) х₂, может обозначаться ;

F₁₁ = х₂  х₁ – обратная импликация;

F₁₂ =  х₁ – отрицание х₁,

F₁₃ = х₁  х₂ – импликация;

F₁₄ = х₁  х₂ – штрих Шеффера;

F₁₅ = 1 – константа единицы.