1.Вступ. Методика статистичної обробки фізичних вимірювань

1. Статистична обробка масиву результатів n прямих вимірювань

Методика статистичної обробки експерименту при визначенні фізичної величини X, яка допускає прямі вимірювання полягає у наступному.

1. За істинне значення фізичної величини X приймається середньоарифметичне значення N вимірювань

(2)

2. Визначається дисперсія величини Х:

(3)

3. Визначається середньоквадратичне відхилення результатів вимірювання від середнього значення :

(4)

4. Визначається границя довірчого інтервалу X при заданій систематичній похибці  (точність приладу, яким вимірюється величина Х). Нехай :

де

,

, ,

Z_N,Р - табличний коефіцієнт Сть'юдента, для N вимірювань та ймовірності P=0.95.

Коефіцієнт Ст'юдента вибирається з Tаблиці 1 за заданими значеннями N та P.

Таблиця І.Коефіцієнт Ст'юдента для ймовірності Р = 0.9; 0.95; 0.99

N	3	4	5	6	7	8	9	10	11	12
ZN,0.9	2.92	2.35	2.13	2.02	1.94	1.90	1.86	1.83	1.81	1.80
ZN,0.95	4.3	3.18	2.78	2.57	2.45	2.36	2.31	2.26	2.23	2.2
ZN,0.99	9.93	5.84	4.06	4.03	7.71	3.50	3.36	3.25	3.17	3.11

Остаточно результат прямого вимірювання записується у вигляді

Х=  Х, P=0,95. (6)

Фізичний зміст виразу (6) полягає у наступному.

З імовірністю Р точне значення величини Х лежить в інтервалі ( - Х; + Х), або у 100*Р випадках із 100 вимірювання величини Х, її точне значення буде знаходитися у інтервалі ( - Х; + Х).

2. Обробка результатів експерименту при посередніх имірюваннях

Нехай шукана фізична величина А визначається функціональною залежністю від k параметрів Х_і

А = f(X₁,X₂,...,X_k). (6)

Спрощена методика статистичної обробки експерименту при вимірюванні фізичної величини А, що є функцією k величин Х_і, які допускають прямі вимірювання й обробляються за методикою п.1, для однакового значення ймовірності Р, полягає у наступному.

1. За істинне значення величини А приймається "середньоарифметичне"

(7)

2. Границя довірчого інтервалу визначається так

(8)

У цьому виразі

,

 частинна похідна від f(X₁,X₂,...,X_k) по змінній ,

 частинна похідна , обчислена для середніх значень параметрів , X_і - границя довірчого інтервалу величини X_і.

Остаточно результат вимірювання записується у вигляді

A=  A, P=0,95. (9)

і має фізичний зміст такий, як і для прямих вимірювань.

3.Метод найменших квадратів

Нехай ми маємо масив N виміряних у досліді значень величин Y,X. Покладемо, що зв'язок Y з X описується у теорії лінійною залежністю

Y=f(X,а,b), (10)

де а та b параметри зв'язку. У результаті потрібно так визначити параметри лінійності а,b, щоб точки, що визначаються масивом знаходилися як можна ближче до прямої. Така задача розв'язується за допомогою метода найменших квадратів.

Він виходить із того, що знайдені середні значення параметрів в (10) повинні забезпечити мінімум відхилення теоретичного значення Y(Xі) від експериментального значення Yі по всіх N точках X_і одночасно, тобто функціонал

. (11)

повинен мати мінімум по параметрах а та b.

Це означає, що величини можна визначити із системи рівнянь

. (12)

Вираз (12) у явному вигляді представляє систему двох рівнянь для визначення двох невідомих . Якщо б залежність (10) містила не два, а К параметрів, то у виразі (12) ми мали б відповідно систему К рівнянь для визначення К невідомих.

Нехай залежність (10) задається лінійною функцією Y=a+bX. Диференціювання Q по а та b дає

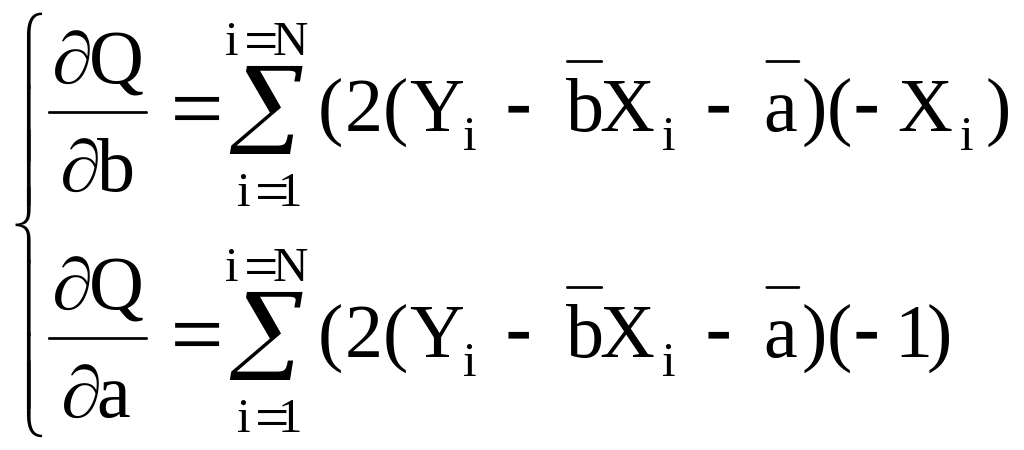. (13)

Якщо в (13) розкрити дужки, то одержимо

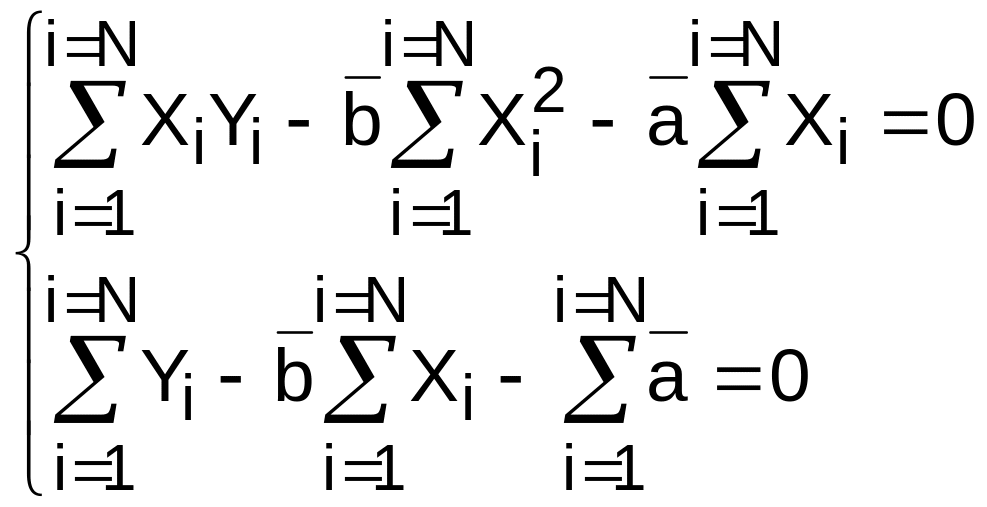. (14).

Якщо в (14) ліві частини поділити на число вимірювань N і ввести середні значення, то одержимо два лінійних рівняння для :

(15).

,

, .

Розв'язок цих рівнянь дає:

, (16).

де

(17)

- коефіцієнт кореляції,

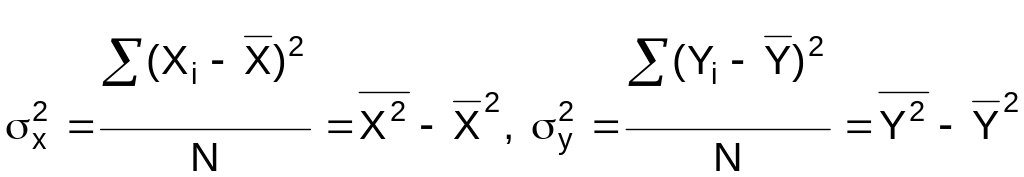(18)

• дисперсії величин X та Y.

За величиною r 1. Якщо r>0, то Y зростаюча, а при r<0 - спадна функція X. Можна показати, що у (11) величина і при r=1 маємо Q=0, тобто експериментальні значення Yі співпадають із теорією. На практиці для встановлення лінійної залежності між відповідними величинами необхідно, щоб значення коефіцієнта r було більше 0.98.

Границі довірчого інтервалу представляються у вигляді

. (19)

Остаточно результат вимірювання запишеться у вигляді

. (20)