6. Случайные погрешности. Функции распределения, виды и параметры распределения случайных величин

Случайная погрешность измерения (сл.п.) — составляющая погрешности измерения, изменяющаяся случайным образом при повторных измерениях одной и той же величины.

Случайная погрешность определяется факторами, проявляющимися нерегулярно с изменяющейся интенсивностью. Значение и знак случайной погрешности определить невозможно, так как в каждом опыте причины, вызывающие погрешность, действуют неодинаково. Случайная погрешность не может быть исключена из результата измерений. Однако проведением ряда повторных измерений и использованием для их обработки методов математической статистики определяют значение измеряемой величины со случайной погрешностью, меньшей, чем для одного измерения.

При организации статистических измерений, для которых и определяется случайная погрешность, создаются условия, характеризующиеся тем, что интенсивность всех действующих факторов доводится до некоторого уровня, обеспечивающего более или менее равное влияние на формирование погрешности. В этом случае говорят об ожидаемой погрешности. Кроме этой погрешности могут иметь место грубые погрешности и промахи.

Грубой погрешностью называют погрешность измерения, существенно превышающую ожидаемую при данных условиях. Причинами грубых погрешностей могут являться неисправность средств измерений, резкое изменение условий измерений и влияющих величин.

Промах — погрешность измерения, которая явно и резко искажает результат. Промах является случайной субъективной ошибкой. Его появление — следствие неправильных действий экспериментатора.

Грубые погрешности и промахи обычно исключаются из экспе­риментальных данных, подлежащих обработке.

Сл. погрешности описываются в метрологии с помощью методов теории вероятностей и математической статистики. При этом физическую величину, результат измерения которой содержит случайную погрешность, и саму случайную погрешность рассматривают как случайную величину. Наиболее распространённые методы: критерий Романовского и критерий 3-х .

подозрительный рез-тат.

выполняется, то подозрительный рез-тат явл. грубой погрешностью и отбрасывается или заменяется средним значением. При этом среднее значение и СКО вычисляются без подозрительного результата.

Это более жёсткий критерий и используется в тех случаях , когда заданная доверительная вероятность равна 0.99.

Математическое описание непрерывных случайных величин осуществляется обычно с помощью дифференциальных законов распределения случайной величины. Эти законы определяют связь между возможными значениями случайной величины (погрешности) и соответствующими им плотностями вероятностей.

Наиболее распространенным при измерениях является нормальный закон распределения. Для некоторой измеряемой величины Х кривая распределения плотности вероятности р(Х) для закона нормального распределения имеет вид:

П

p(X)

Х

ри этом плотность вероятности (или плотность распределения) характеризует плотность, с которой распределяются значения слу­чайной погрешности в данной точке.

Плотность вероятности для закона нормального распределения описывается уравнением

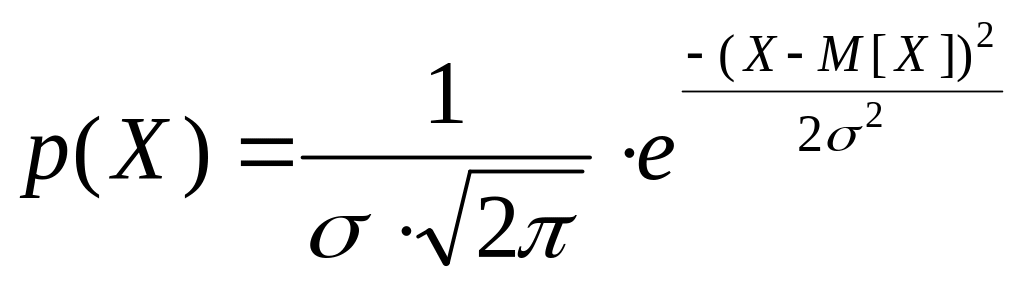
Это распределение характеризуется мат. ожиданием и среднеквадратич. отклонением.

Для практических целей необходимо найти доверительный интервал, который определяется по формуле: = ,

где коэф. Стьюдента, значение которого зависит от числа наблюдений и заданной доверительной вероятности.

При проведении технических измерений, доверительная вероятность задаётся 0.95, это значит, что за установленный интервал может попасть 5% рез-тов измерений, при определении физических констант, при проведении измерений связанных с безопасностью доверит. вероятность устанавливают 0.99.

Критерий ничтожно малой погрешности. Оч. Часто при проведении измерений необходимо учитывать большое кол-во погрешностей, что достаточно сложно. Учёт некоторых погрешностей не вносит сущ-нного влияния на рез-тат , поэтому часто используют критерий ничтожно малой погрешности в соответствии с которой из двух погрешностей одну можно не учитывать, если она в три раза меньше другой, такое допущение приводит к погрешности оценки не более чем 5%.