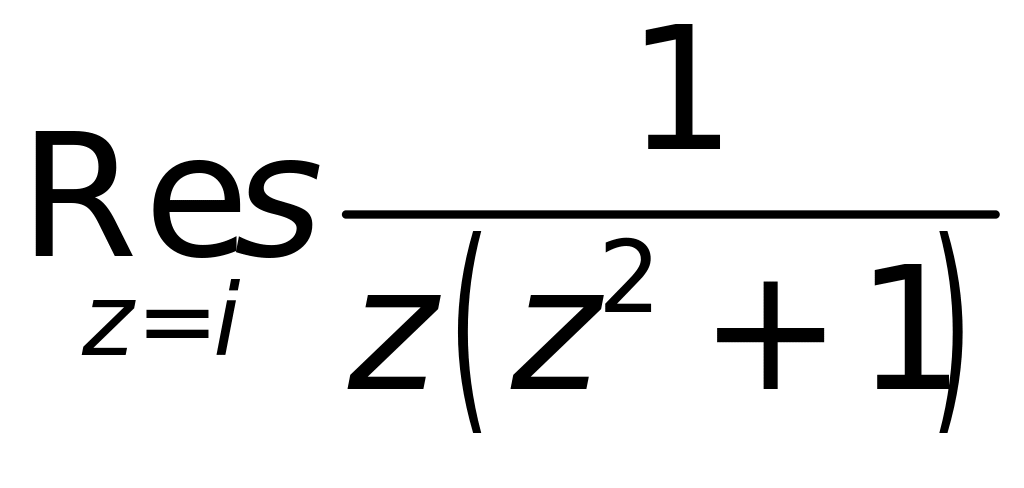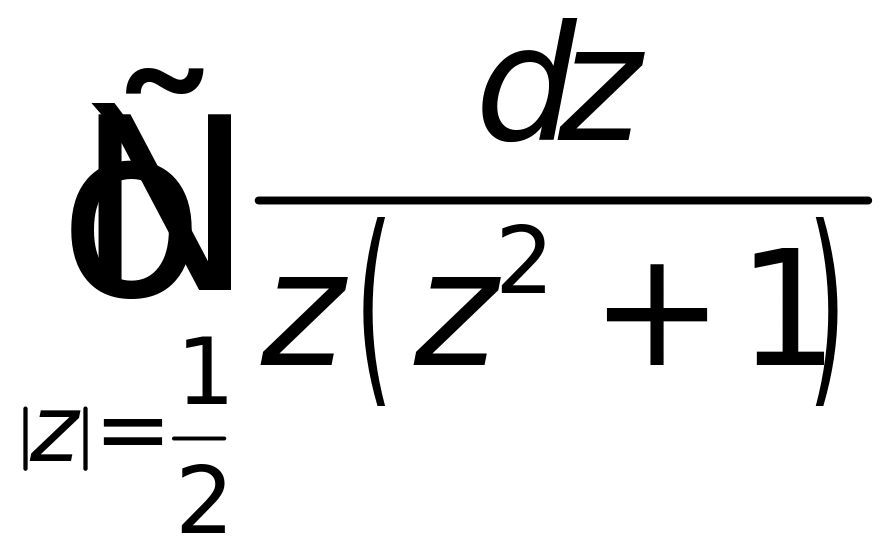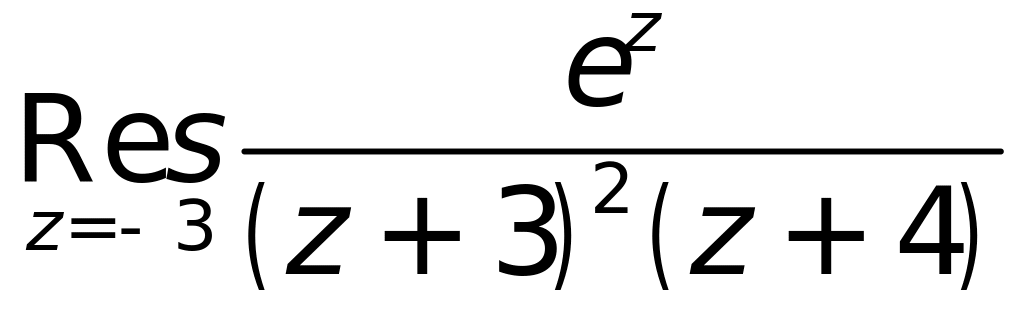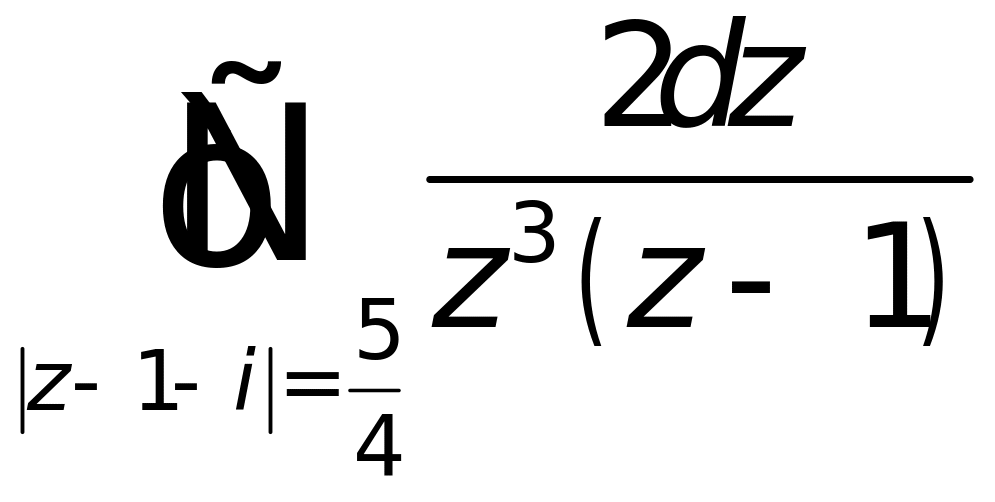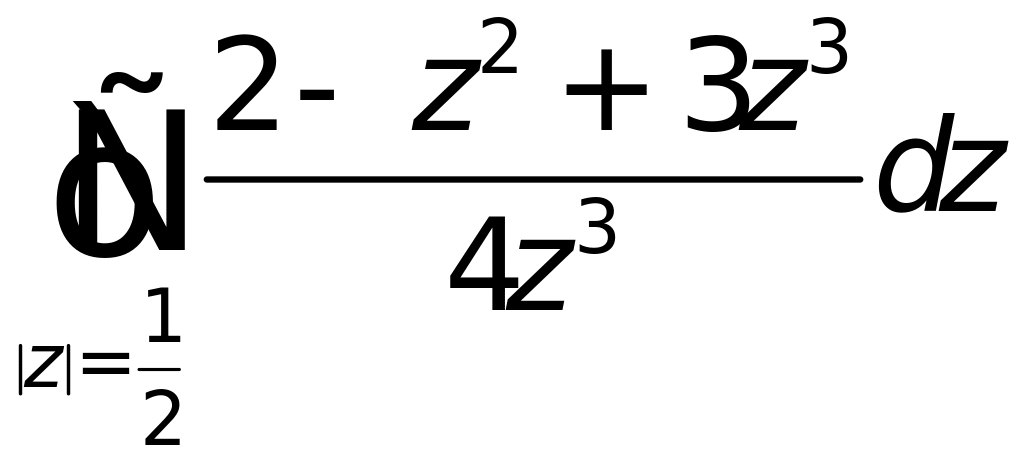- •Контрольная работа «Теория функций комплексного переменного и операционное исчисление» вариант 1
- •2. Даны комплексные числа и
- •2.1 Найти , ;
- •Контрольная работа «Теория функций комплексного переменного и операционное исчисление» вариант 2
- •Контрольная работа «Теория функций комплексного переменного и операционное исчисление» вариант 3
- •Контрольная работа «Теория функций комплексного переменного и операционное исчисление» вариант 4
- •Контрольная работа «Теория функций комплексного переменного и операционное исчисление» вариант 5
- •Контрольная работа «Теория функций комплексного переменного и операционное исчисление» вариант 6
- •Контрольная работа «Теория функций комплексного переменного и операционное исчисление» вариант 7
- •Контрольная работа «Теория функций комплексного переменного и операционное исчисление» вариант 8
- •Контрольная работа «Теория функций комплексного переменного и операционное исчисление» вариант 9
- •Контрольная работа «Теория функций комплексного переменного и операционное исчисление» вариант 10
- •Контрольная работа «Теория функций комплексного переменного и операционное исчисление» вариант 11
- •Контрольная работа «Теория функций комплексного переменного и операционное исчисление» вариант 12
- •Контрольная работа «Теория функций комплексного переменного и операционное исчисление» вариант 13
- •Контрольная работа «Теория функций комплексного переменного и операционное исчисление» вариант 14
- •Контрольная работа «Теория функций комплексного переменного и операционное исчисление» вариант 15
- •Контрольная работа «Теория функций комплексного переменного и операционное исчисление» вариант 16
- •Контрольная работа «Теория функций комплексного переменного и операционное исчисление» вариант 17
- •Контрольная работа «Теория функций комплексного переменного и операционное исчисление» вариант 18
- •Контрольная работа «Теория функций комплексного переменного и операционное исчисление» вариант 19
- •Контрольная работа «Теория функций комплексного переменного и операционное исчисление» вариант 20
- •Контрольная работа «Теория функций комплексного переменного и операционное исчисление» вариант 21
- •Контрольная работа «Теория функций комплексного переменного и операционное исчисление» вариант 22
- •Контрольная работа «Теория функций комплексного переменного и операционное исчисление» вариант 23
- •Контрольная работа «Теория функций комплексного переменного и операционное исчисление» вариант 24
- •Контрольная работа «Теория функций комплексного переменного и операционное исчисление» вариант 25
Контрольная работа «Теория функций комплексного переменного и операционное исчисление» вариант 1
1. Даны комплексные
числа
![]() и
и
![]()
1.1 Найти сумму и
разность чисел
![]() и
и
![]() ;
;
1.2 Найти комплексно сопряжённые числа к числам и ;
1.3 Найти
![]() ,
,
![]() ,
,
![]() ;
;
1.4 Изобразить
числа
,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
и
;
,
и
;
1.5 Найти
![]() ,
,
![]() ,
,
![]() ,
,
![]() и изобразить линии на плоскости
и изобразить линии на плоскости
![]() ;
;
![]() .
.
2. Даны комплексные числа и
2.1 Найти , ;
2.2 Извлечь квадратный
корень из комплексного числа
![]() ;
;
2.3 Возвести
комплексное число
![]() в четвёртую степень;
в четвёртую степень;
2.4 Найти мнимую
часть комплексного числа
![]() ,
если
,
если
![]() .
.
3. Вычертить область, заданную неравенствами:
![]() ;
;
![]() ;
;
![]() .
.
4. Найти в
алгебраической форме значение функции
![]() в заданной точке
в заданной точке
![]() :
:
![]() ;
;
![]() .
.
5. Восстановить
аналитическую в окрестности точки
![]() функцию
функцию
![]() по известной действительной части
по известной действительной части
![]() и значению
и значению
![]() :
:
![]() ;
;
![]() .
.
6. Вычислить интеграл от функции комплексного переменного по данной кривой:
![]() ;
;
![]() .
.
7. Данную функцию
разложить в ряд Лорана в окрестности
точки
.
Определить характер данной точки и
найти вычет в ней:
![]() ;
;
![]() .
.
8. Для данной функции
найти изолированные особые точки и
определить их тип:
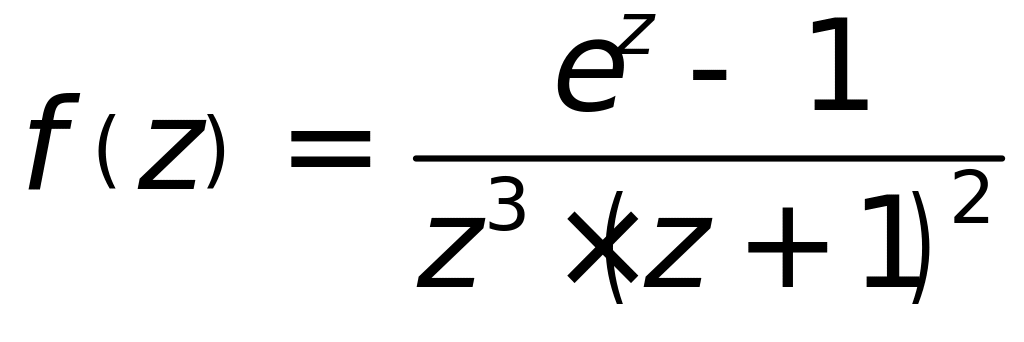
9. Найти значения вычетов в полюсах функций :
а)
|
б)
|
10. Вычислить интегралы:
а)
|
б)
|
11. Найти изображения
данных оригиналов
![]() :
:
а)
|
б)
|
12. По данному графику оригинала найти изображение:
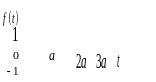
13. Найти оригинал
по заданному изображению:

14. Операционным
методом решить задачу Коши:![]() ,
,
![]() ,
,
![]() .
.
Контрольная работа «Теория функций комплексного переменного и операционное исчисление» вариант 2
1. Даны комплексные
числа
![]() и
и
![]()
1.1 Найти сумму и разность чисел и ;
1.2 Найти комплексно сопряжённые числа к числам и ;
1.3 Найти , , ;
1.4 Изобразить числа , , , , , , и ;
1.5 Найти , , , и изобразить линии на плоскости
;
.
2. Даны комплексные
числа
![]() и
и
![]()
2.1 Найти , ;
2.2 Извлечь квадратный корень из комплексного числа ;
2.3 Возвести комплексное число в четвёртую степень;
2.4 Найти мнимую часть комплексного числа , если .
3. Вычертить область, заданную неравенствами:
![]() ;
;
![]() ;
;
![]() .
.
4. Найти в алгебраической форме значение функции в заданной точке :
![]() ;
;
![]() .
.
5. Восстановить
аналитическую в окрестности точки
функцию
по известной мнимой
![]() и значению
:
и значению
:
![]() ;
.
;
.
6. Вычислить интеграл от функции комплексного переменного по данной кривой:
![]() ;
;
![]() .
.
7. Данную функцию
разложить в ряд Лорана в окрестности
точки
.
Определить характер данной точки и
найти вычет в ней:
![]() ;
;
![]() .
.
8. Для данной функции
найти изолированные особые точки и
определить их тип:
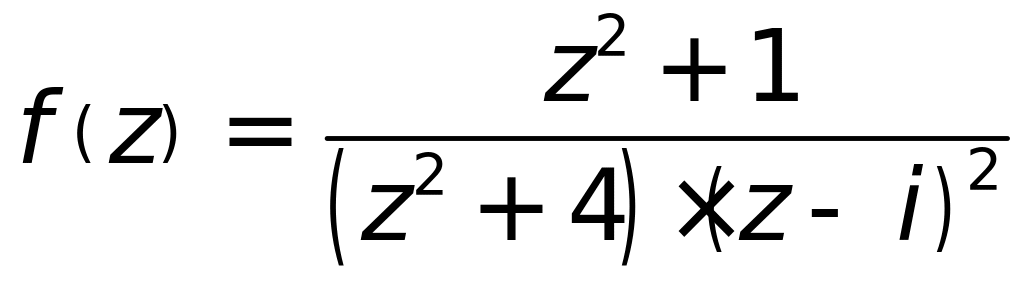
9. Найти значения вычетов:
а)
|
б)
|
10. Вычислить интегралы:
а)
|
б)
|
11. Найти изображения данных оригиналов :
а)
|
б)
|
12. По данному графику оригинала найти изображение:
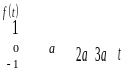
13. Найти оригинал
по заданному изображению:

14. Операционным методом решить задачу Коши:
![]() ,
,
![]() ,
,
![]() .
.