Самостоятельная работа.

1. Средний диаметр подшипников должен составлять 35 мм. Однако для выборки из 82 подшипников он составил 35,3 мм при выборочном среднем квадратичном отклонении 0,1 мм. При 5%-м уровне значимости проверить гипотезу о том, что станок, на котором изготавливают подшипники, не требует подналадки.

2. Поставщик удобрений утверждает, что применение новой партии удобрений обеспечивает урожайность пшеницы в 60 ц/га. Удобрения внесли на площадь в 37 га и получили урожай 55 ц/га при выборочном среднем квадратичном отклонении 3 ц/га. При 5%-м уровне значимости оценить справедливость утверждения поставщика.

3. Среднесуточная продажа хлеба в течение многих лет для данного магазина составляла 6 т при среднем квадратичном отклонении 0,05 т. Сегодня магазином было продано 7 т хлеба. Можно ли при 5%-м уровне значимости предполагать, что и завтра будет продано 7 т хлеба?

Задача. Фирма – изготовитель женских украшений, выпустив новый товар, утверждает, что 40% покупателей купят эти украшения. В ходе 10-дневной рекламной распродажи в среднем приобрели украшения 29,5% покупателей, выборочное среднее квадратичное отклонение составило 16,5%. При 5%-м уровне значимости оценить утверждение изготовителя товара.

Решение: Проверим нулевую гипотезу : = 40% и альтернативную

: < 40%. Предположим, что случайная величина Х – число покупателей – имеет нормальный закон распределения. В данной задаче требуется проверит гипотезу о числовом значении математического ожидания нормального распределения при неизвестной дисперсии. Критерий имеет вид T = .

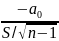Для заданного уровня значимости = 0,05 найдем левостороннюю критическую область с учетом того, что = 10 – 1 = 9 степеней свободы (см. Приложение 6). Критическая область есть интервал (- -1,833). Вычислим : = = -1.909.Число -1,909 попадает в критическую область. Таким образом, нулевая гипотеза отвергается.

Самостоятельная работа.

1. Поставщик двигателей утверждает, что средний срок их службы равен 800 ч. Для выборки из 17 двигателей средний срок службы оказался равным 865 ч при выборочном среднем квадратичном отклонении 120 ч. Проверить нулевую гипотезу при уровне значимости: а) 5% ; б) 1%.

2. По результатам 10 замеров установлено, что среднее время обслуживания мастером клиента = 15 мин. Предполагая, что время обслуживания клиента – нормально распределенная случайная величина с дисперсией = 9 ,при уровне значимости = 0,05 установить, можно ли принять в качестве норматива (математического ожидания) для обслуживания одного клиента: а) 21 мин; б) 16 мин.

3. По паспортным данным на автомобильный двигатель, расход топлива на 100 км пробега составляет 10 л при среднем квадратичном отклонении 2 л. В результате совершенствования конструкции ожидается, что расход топлива уменьшится. Для проверки проведены испытания 25 случайно отобранных автомобилей с модернизированным двигателем: средний расход топлива 100 км пробега составил 9,2 л. Используя 5%-й уровень значимости, проверить гипотезу, утверждающую, что модернизация повлияла на расход топлива.

4. Из большой партии ананасов одного размера случайным образом отобрано 36 штук. Выборочная средняя масса одной штуки при этом оказалась равной 930 г. Используя двусторонний критерий при , проверить гипотезу, что средняя масса одного ананаса (по утверждению поставщика) составляет 1 кг. ,если: а) Среднее квадратичное отклонение известно и составляет 200 г; б) Среднее квадратичное отклонение неизвестно, а выборочное 250 г.