Тема 2.?. Проверка статистических гипотез.

Если принятое решение о законе распределения генеральной совокупности или о числовых значениях его параметров проверяется по выборочным данным, то говорят о проверке статистических гипотез. Проверке подвергается гипотеза об отсутствии разности между принятым и найденным по выборке значениями исследуемого параметра. Такую гипотезу называют нулевой. Противоположную ей гипотез называют альтернативной.

2.Схема проверки нулевой гипотезы:

1. Рассматривая выборочные данные х₁, х₂, …, х_n и учитывая конкретные условия задачи, принимают Н₀ – нулевую гипотезу и Н₁ – альтернативную гипотезу, конкурирующую с Н₀.

2. Так как решение о справедливости гипотезы Н₀ принимается на основе выборочных данных, могут возникать ошибки двух родов:

- гипотеза Н₀ отвергается, а на самом деле она верна – это ошибка первого рода; вероятность ошибки первого рода равна уровню значимости , т.е.

= Р (Н₁);

- гипотеза Н₀ принимается, а на самом деле она неверна – это ошибка второго рода; вероятность ошибки второго рода равна , т.е. = Р (Н₀) .

Соответственно, вероятность принять верную гипотезу равна

Р (Н₀) = 1 – , а вероятность отвергнуть неверную гипотезу Н₀ равна Р (Н₁) – 1 – .

3. Используя выборочные данные, вводят статистический критерий – некоторую функцию К, зависящую от условий решаемой статистической

задачи. Эти функции, являясь случайными величинами, подчинены некоторому известному, затабулированному закону распределения (t-распределение, ² – распределение или нормальное распределение).

В зависимости от принятого уровня значимости из области допустимых значений функции критерия К выделяют критическую область . Далее руководствуются следующим правилом: если вычисленное по выборке значение критерия К попадают в критическую область, то Н₀ справедлива и, следовательно, совершена ошибка первого рода, вероятность которой , т.е. Р(К ) = .

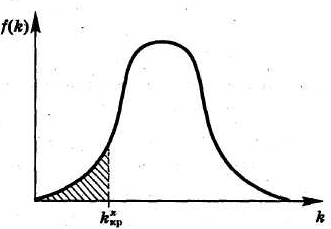
Возможны три варианта расположения критической области:

правосторонняя критическая область (рис. 1, а), состоящая из интервала ( , ), где определяется из условия Р(К ) = ;

левосторонняя критическая область (рис 1, б), состоящая из интервала

(- ), где определяется из условия Р(К ) = ;

двусторонняя критическая область (рис..1, в), состоящая из интервалов (- ) и ( , ), где точки определяются из условий Р(К ) = /2 и Р(К ) = /2.

4. По выборочным данным находят числовое значение критерия ( ). Если попадает критическую область , то гипотеза Н₀ отвергается и принимается альтернативная гипотеза Н₁. Если не попадает в критическую область, то гипотеза Н₀ принимается.

При проверке статистических гипотез учитываются конкретные условия рассматриваемой задачи.

3.Сравнение выборочной средней с математическим ожиданием

На практике часто требуется оценить соответствуют ли в действительности рекламные данные о параметрах того или иного товара. В этом случае возникает задача сравнения выборочной средней с анонсируемым значением этого параметра.

Задача. Фирма-поставщик в рекламном буклете утверждает, что средний срок безотказной работы предлагаемого изделия – 2900 ч. Для выборки из 50 изделий средний срок безотказной работы оказался равным 2720 ч при выборочным среднем квадратичном отклонении 700 ч. При 5%-м уровне значимости проверить гипотезу о том, что значение 2900 ч является математическим ожиданием.

Решение. Предположим, что случайная величина срока безотказной работы подчинена нормальному закону распределения. Требуется проверить гипотезу о числовом значении математического ожидания нормально-распределённой величины (генеральной средней) при неизвестной генеральной дисперсии. В этом случае в качестве критерия выбирают функцию Т= , где - выборочная средняя, а₀ – математическое ожидание, S – выборочное среднее квадратичное отклонение. Случайная величина Т имеет t-распределение (распределение Стьюдента) с = n-1 степенями свободы. В данной задаче речь идёт о сравнении выборочной средней 2720 ч с гипотическими математическим ожиданием ₀ = 2900 ч, при этом выборочная среднее квадратичное отклонение равно 700 ч.

Требуется найти критическую область для нулевой гипотезы Н₀: а₀ = 2900 при альтернативной гипотезе Н₁: а₀ 2900. Очевидно, что другие альтернативные гипотезы (а₀ 2900 и а₀ 2900) нецелесообразный, так как потребитель обычно обеспокоен лишь тем, что срок службы изделия может оказаться меньше гарантируемого поставщиком.

Критическая область левосторонняя; находим из условия Р(T ) = a. При = 0,05 и = 50-1 = 49 в таблице t-распределения (см. Приложение 6), используя линейную интерполяцию, находим = - = -1,677. Таким образом, критическая область = (- , -1,677). Рассчитаем t_r1 полагая а₀ = ₀:

t_r = = = -1,8.

Значение -1,8 попадает в критическую область, поэтому нулевая гипотеза Н₀ должна быть отвергнута. Следовательно, фирма в рекламе завышает срок безотказной работы изделия.

Задача. Составлена случайная выборка из 64 покупателей, которые интересовались товаром А. Из них товар А купили 16 человек. Поставщик утверждает, что данный товар дожжен привлечь треть покупателей, а среднее квадратическое отклонение _х равно одному человеку. Проверить нулевую гипотезу при 5%-м уровне значимости.

Решение: Предположим, что число покупателей, приобретающих товар А, есть случайная величина, подчинённая нормальному закону распределения. Гипотетическая генеральная средняя при этом составит 21 человек (64* ). Будем считать, что

_х = 1. Таким образом, речь идёт о проверке гипотезы о числовом значении математического ожидания нормального распределения при известной дисперсии, т.е. о сравнении гипотетической генеральной средней 21 с выборочной средней 16 при известном среднем квадратичном отклонении _х. Нулевая гипотеза в этой задаче имеет вид Н₀:а₀ = 21, а альтернативная, например, Н₁:а₀ 21 или Н₁:а₀ 21. Уровень значимости задан: В качестве критерия в этом случае рассматривается функция Z = . Функция Z подчинена нормальному закону распределения N(0,1). Критическая область будет двусторонней, её образуют интервалы (- и ( , ) , определяемые из условий Р(Z ) = /2 и P(Z ) = .

Если Это вероятность попадания случайной величины Z в левостороннюю или правостороннюю критическую область

(1- ) можно представить следующим образом:

P(- ) = Р(- + P(0 ) = 1 – .

Так как Р(- = 0,5, а P(0 ) = Ф( ) – функция Лапласа в точке , то Ф( ) = 1- - 0,5 = 0,475. На основании таблицы значений функции Лапласа (см. Приложение 2) находим - 1,96. Точка расположена симметрично и равна -1,96. Следовательно, критическая область состоит из интервалов (- . Рассчитаем z_r: Z_r = = -40.

Значение z_r попадает в критическую область, поэтому гипотеза Н₀:а₀ = 21 отвергается.