6 Методические рекомендации по расчету трехфазных цепей

Пример 1. В трехфазную сеть с линейным напряжением U_л = 220 В включен приемник, соединенный треугольником, сопротив­ление каждой фазы которого Z = (10+j10) Ом (рис. 9). Найти то­ки в каждой фазе нагрузки и линии и показания каждого ваттмет­ра. Построить векторную диаграмму. Найти те же величины в слу­чае обрыва цепи в точке d.

Решение. Расчет токов в трехфазных цепях производится комп­лексным методом. Примем, что вектор линейного напряжения U_АВ направлен по действительной оси, тогда

U_AB = U_ab = 220 B; U_BC = U_bc = 220e^-j120˚ B; U_CA = U_ca =220e^j120˚ B.

Рис. 9.

Определяем фазные токи:

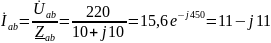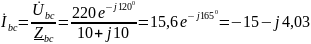(A)

(A);

.

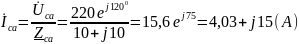Находим линейные токи:

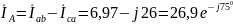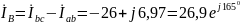A;

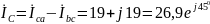A;

A.

Определим показания ваттметров:

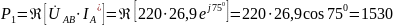Вт

Вт.

Активная мощность цепи (алгебраическая сумма показаний ваттметров) Р равна:

Р = Р₁ + Р₂ = 1530 + 5730 = 7260 Вт.

Рис. 10

Пример 2. В четырехпроводную трехфазную сеть с линейным на­пряжением U_л = 220 В включен звездой приемник, активные и индук­тивные сопротивления фаз которого соответственно равны: r_а = 3 Ом, х_а = 4 Ом, r_b = 3 Ом, x_b = 5,2 Ом, r_с = 4 Ом, х_с = 3 Ом

(рис. 11). Определить токи в линейных и нейтральном проводах и построить векторную диаграмму.

Решение. Считаем, что вектор фазного напряжения U_А направлен по действительной оси, тогда

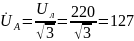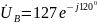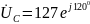В, B, B

Рис. 11 Рис.12

Находим линейные токи:

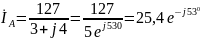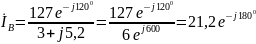A;

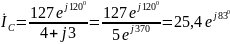A;

A.

Ток в нейтральном проводе определяется как геометрическая сумма линейных токов:

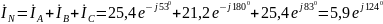A

Векторная диаграмма показана на рис. 12.

При несимметричной нагрузке для определения активной мощности находят мощность каждой фазы отдельно:

P_ф = U_ф I_ф cos φ,

а мощность трехфазной системы получают как сумму мощностей всех фаз или используют схему включения двух ваттметров.

Пример 3. В трехфазную сеть с линейным напряжением U_л = = 380 В включен звездой приемник, активное, индуктивное и емкостное сопротивление фаз которого равны: r = х_L = x_C = 22 Ом (рис. 13).

Рис. 13 Рис. 14

Решение. Расчет токов производится комплексным методом. Находим фазные напряжения:

В; ;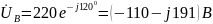

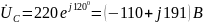
Определяем напряжение между нейтральными точками приемника и источника питания:

.

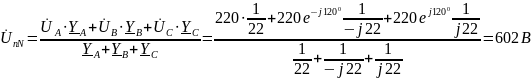Определяем напряжения на зажимах фаз приемника:

U_an = 220 - 602 = – 382 B;

U_bn = (-110 - j191) – 602 = (-712 – j191) B;

U_cn = (-110 + j191) – 602 = (- 712 + j191) B.

Определяем фазные (линейные) токи:

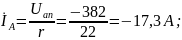
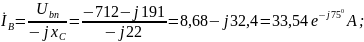
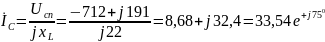A;

Правильность расчета токов проверяем по первому закону Кирхгофа:

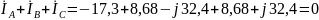
Векторная диаграмма изображена на рис. 14.

Из рассмотрения этой задачи следует, что напряжения на зажимах фаз приемника получаются неодинаковыми. Поэтому несимметричные приемники (бытовые и др.) соединяют либо четырехпроводной звездой, либо треугольником.