Алгоритми виявлення місця та величини спотворень

Алгоритм табличного виявлення місця та величини спотворень. Виходячи із властивості коду про наявність однозначного зв’язку можна побудувати та використати таблицю відповідності типу → та здійснити виправлення цього спотворення.

При цьому слід мати на увазі, що процедури виявлення і виправлення спотворень у циклічних кодах витікають із загальних властивостей корегуючих кодів і ґрунтуються на аналізі залишків від ділення прийнятої комбінації 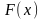на багаточлен , який утворює цей код.

Слід врахувати, що максимальна кількість можливих залишків при розподілі на багаточлен ступеня k є завжди меншим значення 2^k при максимальному значенні залишку, яке дорівнює (2^k – 1). Це означає, що і максимальна кількість спотворень, а отже і довжина коду п повинні відповідати умові

, (1)

інакше неминучим є повторення значень залишків. Останнє призводить до явища, коли при порушенні нерівняння (1) спотворенням у різних символах інформаційного об’єкті будуть відповідати залишки, які хоча і відрізняються від нуля, але є однаковими. Таким чином при порушенні нерівняння (1) код виявляє наявність спотворення, але є нездатним виявити їх місце та величину, отже є нездатним до їх виправлення.

Із виразу (1) неважко визначити ступінь утворюючого поліному, який потрібно застосовувати для виявлення і виправлення спотворень в інформаційному об’єкті загальною довжиною п символів:

. (2)

Якщо умови (1) та (2) дотримано, то як елементи цієї таблиці використовують результати розподілу х_і/Р(x), які для прикладу при Р(x) = х³ + х² + х⁰ та і = 0, 1,…, 6 зведено в таблицю 2.

Таблиця 2

Показник ступеня хі	Значення Е = хі	Результат розподілу хі/Р(x)	Двійковий еквівалент хі/Р(x)
0	х0 =1	х0=1	001
1	х1	х1	010
2	х2	х2	100
3	х3	х2 + 1	101
4	х4	х2 + х + 1	111
5	х5	х + 1	011
6	х6	х2 +х	110

Звернемо увагу, що в цьому прикладі умова (2) має вигляд і задовольняється при . Така таблиця є основою першого, табличного, алгоритму виявлення та виправлення спотворень на основі циклічного коду.

Алгоритм пошуку і виправлення помилкових розрядів будується виходячи із тих же міркувань, що результат ділення прийнятої комбінації F(x) та ділення відповідного спотворення на утворюючий поліном є еквівалентними. Тоді можна застосувати пошук і виправлення помилкових розрядів в n- елементній комбінації (n = m + k), включаючи такі кроки:

1. Отримуємо залишок від ділення E_п, відповідного спотворенню в старшому розряді [100…00], на утворюючий поліном : R₀(x) =E_і (x)/ .

2. Ділимо отриманий поліном на і одержуємо поточний залишок R(x).

3. Порівнюємо R₀(x) і R(x).

• Якщо вони рівні, то спотворення сталася в старшому розряді.

• Якщо ні, то збільшуємо ступінь прийнятого полінома на x і знову проводимо розподіл: •x/ = R(x).

4. Знову порівнюємо отриманий залишок з R₀(x).

• Якщо вони рівні, то спотворення в другому розряді.

• Якщо ні, то множимо •х² і повторюємо ці операції до тих пір, поки R(x) не буде дорівнює R₀(x). Спотворення буде в розряді, відповідному числу, на яке підвищений ступінь , плюс один. Наприклад: •x³/ = R₀(x), тоді спотворення в розряді із номером (3 + 1) = 4.