Задание № 3

Решение:

1. Определим ошибку выборки средней оптовой цены реализованной продукции и границы, в которых она будет находиться в генеральной совокупности.

Формула предельной ошибки при механическом отборе:

, где t – критерий Стьюдента, - дисперсия по выборке, n – объём выборки, - коэффициент выборки.

В нашем случае:

=3,00 (по результатам задания 1)

= 5% = 0,05 (по условию).

При вероятности Р = 0,997 t = 3.

= руб.

Искомый доверительный интервал определим по формуле:

,

Следовательно, с вероятностью 0,997 средняя оптовая цена в генеральной совокупности будет находится в пределах:

руб.,

2. Определим ошибку выборки доли организаций с оптовой ценой реализации продукции 17 руб. и более и границы, в которых будет находиться генеральная доля.

Ошибка выборки для доли определяется по формуле:

,

где

В нашем случае m - число организаций с оптовой ценой реализации продукции 17 руб. и более равно 8

= 0,27;

Границы, в которых будет находиться генеральная доля организаций с оптовой ценой реализации продукции 17 руб. и более:

;

Следовательно в генеральной совокупности доля организаций с оптовой ценой реализации продукции 17 руб. и более будет составлять от 4 до 50%. Такие широкие границы обусловлены большой вероятностью, с которой необходимо гарантировать предельную ошибку.

Задание № 4

Решение:

Имеются следующие данные о реализации продукции торго­вой организацией:

Продукция	Цена за 1 шт, руб.		Объем реализации, тыс. шт.
	базисный,	отчетный,	базисный,	отчетный,
А	45	50	130	200
Б	65	55	140	100

1. Индексы цен по каждому виду продукции.

Индивидуальный индекс цен вычисляется по формуле

Этот индекс показывает, во сколько раз увеличилось (уменьшилось) цена одного товара в отчетном периоде по сравне­нию с базисным, или сколько процентов составляет рост (сниже­ние) цен какого-либо одного товара. Подставляя значения, получим:

Для продукции А: цена увеличилась 11%.

Для товара Б: цена снизилась на 15,4%.

По двум видам продукции вместе.

Среднее относительное изменение цен на продукцию в целом и за счет отдельных факторов определяется системой индексов переменного состава, постоянного состава и структурных сдвигов:

Индекс переменного состава

Индекс постоянного состава

Индекс структурных сдвигов

Здесь - доли структуры в общей массе.

При этом сумма абсолютных приростов (убыли) среднего уровня цен в целом и за счет отдельных факторов определяются как разница между числителем и знаменателем соответствующих индексов:

- характеризует влияние двух факторов вместе;

- влияние фактора изменения цены по отдельным видам продукции на среднее изменение цен;

- влияние фактора изменения структуры реализованной продукции на среднее изменение цен.

Для автоматизации вычислений все расчеты будем проводить в MS Excel. Формульные шаблоны расчетных таблиц приведены на рис. 2.6, Результаты расчетов в таблице 2.6.

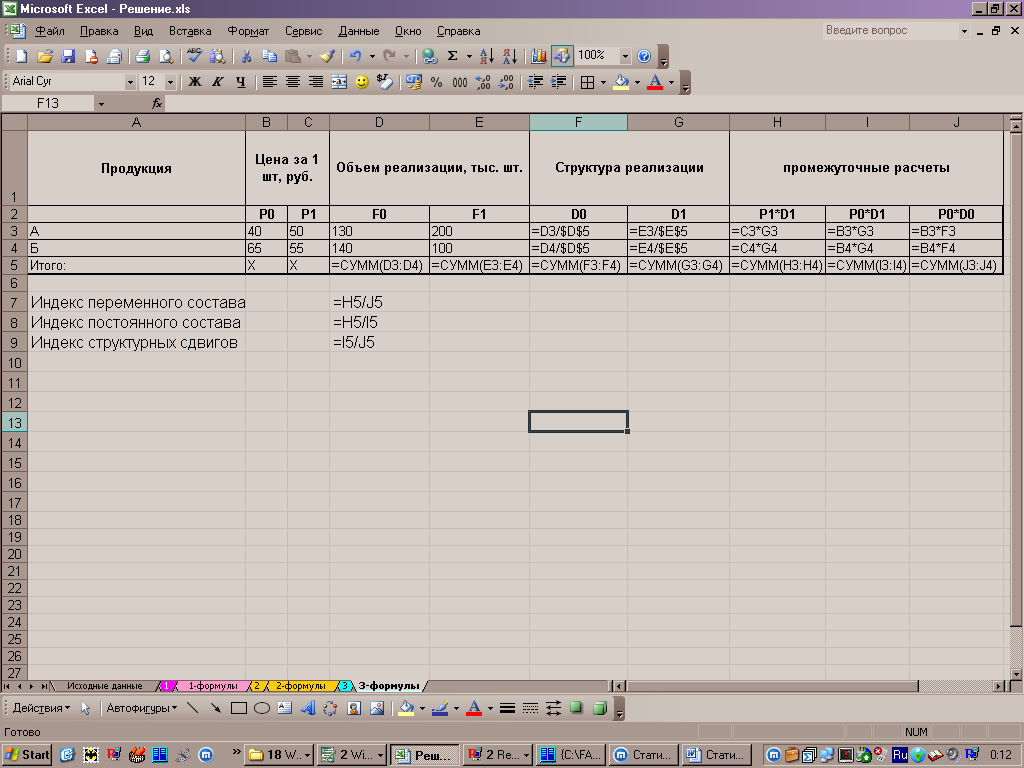
Рис. 2.6. Формульный шаблон расчетной таблицы 2.6.

Таблица 2.6.

Результаты расчетов

Продукция	Цена за 1 шт, руб.		Объем реализации, тыс. шт.		Структура реализации		промежуточные расчеты
	P0	P1	F0	F1	D0	D1	P1*D1	P0*D1	P0*D0
А	40	50	130	200	0,481	0,667	33,33	26,67	19,26
Б	65	55	140	100	0,519	0,333	18,33	21,67	33,70
Итого:	Х	Х	270	300	1,000	1,000	51,67	48,33	52,96

Таким образом, индекс переменного состава равен:

(97,6%)

Индекс постоянного состава (107%)

Индекс структурных сдвигов (91,3%)

Абсолютное изменение среднего уровня цен:

За счет обоих факторов: руб.

За счет фактора изменения цен по отдельным видам продукции руб.

За счет фактора изменения структуры: .

Выводы. В отчетном периоде по сравнению с базисным, в данной торговой организации, средняя цена реализации продукции А и Б снизилась на 2,4%, что составило 1,29 руб.

При этом за счет только изменения цен на реализованную продукцию средняя цена возросла на 7%, что составило 3,34 руб. Однако за счет изменения структуры реализации средняя цена снизилась на 4,63 руб, что составило 8,7%.