1 Билет.

Электрический заряд, источник электромагнитного поля, связанный с материальным носителем; внутренняя характеристика элементарной частицы, определяющая её электромагнитные взаимодействия. Э. з. — одно из основных понятий учения об электричестве. Вся совокупность электрических явлений есть проявление существования, движения и взаимодействия Э. з.

Различают 2 вида Э. з., условно называемые положительным и отрицательным; при этом одноимённо заряженные тела (частицы) отталкиваются, а разноимённо заряженные притягиваются (впервые установлено Ш. Ф. Дюфе в 1733—34). Заряд наэлектризованной стеклянной палочки назвали положительным, а смоляной (в частности, янтарной) — отрицательным. В соответствии с этим условием Э. з. электрона (электрон по-гречески — янтарь) отрицателен. Э. з. дискретен: существует минимальный, элементарный электрический заряд, которому кратны все Э. з. тел. Полный Э. з. замкнутой физической системы, равный алгебраической сумме зарядов слагающих систему элементарных частиц (для обычных макроскопических тел — протонов и электронов), строго сохраняется во всех взаимодействиях и превращениях частиц системы (см. Заряда сохранения закон). Сила взаимодействия между покоящимися заряженными телами (частицами) подчиняетсяКулона закону. Связь Э. з. с электромагнитным полем определяется Максвелла уравнениями.

В Международной системе единиц Э. з. измеряется в кулонах.

Зако́н Куло́на — это закон, описывающий силы взаимодействия между точечными электрическими зарядами.

Был открыт Шарлем Кулоном в 1785 г. Проведя большое количество опытов с металлическими шариками, Шарль Кулон дал такую формулировку закона:

Модуль силы взаимодействия двух точечных зарядов в вакууме прямо пропорционален произведению модулей этих зарядов и обратно пропорционален квадрату расстояния между ними

Иначе: Два точечных заряда в вакууме действуют друг на друга с силами, которые пропорциональны произведению модулей этих зарядов, обратно пропорциональны квадрату расстояния между ними и направлены вдоль прямой, соединяющей эти заряды. Эти силы называются электростатическими (кулоновскими).

Важно отметить, что для того, чтобы закон был верен, необходимы:

1. точечность зарядов — то есть расстояние между заряженными телами много больше их размеров — впрочем, можно доказать, что сила взаимодействия двух объёмно распределённых зарядов со сферически симметричными непересекающимися пространственными распределениями равна силе взаимодействия двух эквивалентных точечных зарядов, размещённых в центрах сферической симметрии;

2. их неподвижность. Иначе вступают в силу дополнительные эффекты: магнитное поле движущегося заряда и соответствующая ему дополнительная сила Лоренца, действующая на другой движущийся заряд;

3. взаимодействие в вакууме.

Однако с некоторыми корректировками закон справедлив также для взаимодействий зарядов в среде и для движущихся зарядов.^[1]

В векторном виде в формулировке Ш. Кулона закон записывается следующим образом:

где   — сила, с которой заряд 1 действует на заряд 2;   — величина зарядов;   — радиус-вектор (вектор, направленный от заряда 1 к заряду 2, и равный, по модулю, расстоянию между зарядами —  );   — коэффициент пропорциональности. Таким образом, закон указывает, что одноимённые заряды отталкиваются (а разноимённые — притягиваются).

Электростатическое поле — поле, созданное неподвижными в пространстве и неизменными во времени электрическими зарядами (при отсутствии электрических токов).

Электрическое поле представляет собой особый вид материи, связанный с электрическими зарядами и передающий действия зарядов друг на друга.

Если в пространстве имеется система заряженных тел, то в каждой точке этого пространства существует силовое электрическое поле. Оно определяется через силу, действующую на пробный заряд, помещённый в это поле. Пробный заряд должен быть малым, чтобы не повлиять на характеристику электростатического поля.

Свойства:

1. Всегда незамкнуты: начинаются на положительных и заканчиваются на отрицательных зарядах

2. Не пересекаются

3. Густота линий тем больше, чем больше напряженность, то есть напряженность поля прямо пропорциональна количеству силовых линий, проходящих через единицу площади поверхности

электростатическое поле оказывается потенциальным полем. (  в этом случае - случае электростатики - принято называть электростатическим потенциалом).

• Также и обратно 

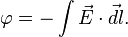
Уравнения поля (уравнения Максвелла) при этом также сильно упрощаются (уравнения с магнитным полем можно исключить, а в уравнение с дивергенцией можно подставить  ) и сводятся к уравнению Пуассона:

а в областях, свободных от заряженных частиц - к уравнению Лапласа:

Учитывая линейность этих уравнений, а следовательно применимость к ним принципа суперпозиции, достаточно найти поле одного точечного единичного заряда, чтобы потом найти потенциал или напряженность поля, создаваемого любым распределением зарядов (суммируя решения для точечного заряда).

Очень полезной в электростатике оказывается теорема Гаусса, содержание которой сводится к интегральной форме единственного нетривиального для электростатики уравнения Максвелла:

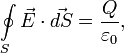
где интегрирование производится по любой замкнутой поверхности S (вычисляя поток   через эту поверхность), Q - полный (суммарный) заряд внутри этой поверхности.

Эта теорема дает крайне простой и удобный способ расчета напряженности электрического поля в случае, когда источники имеют достаточно высокую симметрию, а именно сферическую, цилиндрическую или зеркальную+трансляционную. В частности, таким способом легко находится поле точечного заряда, сферы, цилиндра, плоскости.