Ответы на билеты за 2008 год (doc) / Билет27

Билет№27. Дайте определение разрешимого множества, приведите примеры. Докажите теорему о свойствах замкнутости класса разрешимых множеств.

Определение: множество называется разрешимым, если его характеристическая функция вычислима.

; 1 – если n принадлежит А, 0 – если не принадлежит А.

Примеры:

N, , r(чётные), Н (нечётные), простые числа.

Теорема о замкнутости класса разрешимых множеств:

Если множество А, В – разрешимы, то разрешимы так же их объединения, их пересечения, декартово произведение.

1. докажем разрешимость множества 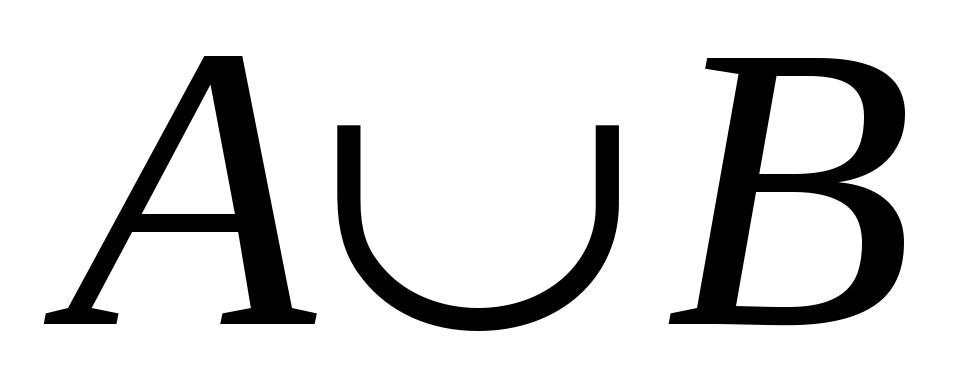- это следует из того, что

Множество (нат. чисел) называется перечислимым, если оно является множеством значений нек выч функции.