Подобие треугольников. Первый признак подобия

Примечание. Это урок с задачами по геометрии о подобии треугольников. Здесь размещены задачи, которые вызывают трудности при решении. Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме.

Задача

В треугольнике ABC угол A вдвое больше угла B, а длины противолежащих этим углам сторон соответственно равны 12 и 8. Найти третью сторону. 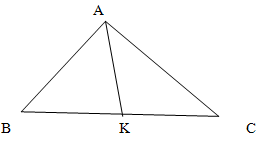  Решение. Для угла А построим биссектрису на противоположную сторону BC. Пусть она пересечет противоположную сторону в точке К. Исходя из того, что AK -  биссектриса, углы ABC и KAC - равны. Поскольку угол С у них общий, то и третий угол этих треугольников является одинаковым. Таким образом, треугольники являются подобными по трем углам. Исходя из того, что треугольники ABC и AKC подобны: AC : BC = KC : AC = AK : AB AC : BC = KC : AC 8 / 12 = KC / 8 KC = 64 / 12 = 16 / 3 Поскольку угол AKB = ABK (BK - биссектрисса, следовательно - треугольник AKB равнобедренный) Откуда AK = BK Учтем, что BK = AC - KC, тогда AK = BK = 12 - 16 / 3 Теперь вернемся к свойствам подобных треугольников KC : AC = AK : AB и подставим известные значения (16 / 3 ) / 8 = ( 12 - 16 / 3 ) / AB AB =  (AK * AC) / KC = 10 Ответ: 10 см

Подобие треугольников. Третий признак подобия

В этом уроке, вы найдете решение задач по геометрии, которые используют правила подобия треугольников и являются интересными для решения. Я их размещаю здесь если они вызывают некоторые трудности при решении у школьников.

Задача

Треугольники ABC и A₁B₁C₁ подобны. Соотношение сторон теругольников 3:4 . Площадь одного из них больше площади другого на 14 см². Найдите площади треугольников.

Решение

Для решения данной задачи будем руководствоваться основным свойством подобия треугольников - все размеры одного теругольника подобны размерам другого. Сначала опустим на сторону а каждого треугольника высоту h. Таким образом площадь первого треугольника будет выражаться формулой S₁=1/2ah, а площадь второго треугольника формулой S₂=1/2*3/4a*3/4h. Таким образом, можно определить соотношение площадей треугольников:

S₁/S₂ = 1/2 ah / ( 1/2 * 9/16 ah)

S₁/S₂ = ah / ( 9/16 ah)

S₁/S₂ = 16/9

Выше перечисленные преобразования мы могли бы не проводить, если нам известна теорема: "площади подобных треугольников относятся как квадрат соотношения их сторон"

Выразим площадь одного треугольника через площадь другого:

S1=16S₂/9

По условию задачи S₁-S₂=14, таким образом

16S₂/9-S₂=14

7/9S₂=14

S₂=18, следовательно S₁ = 14+18=32

Ответ: 18 и 32

Задача

Стороны AB и DC трапеции ABCD продлили так, что прямые AB и DC пересеклись в точке E. Таким образом, продолжения сторон трапеции образовали треугольник площадью 98 квадратных сантиметров. Найти площадь трапеции, если ее основания относятся друг к другу как 5 к 7.

Решение

Начало решения. Из условия задачи видно, что у нас получились треугольники EAD и EBC. Поскольку оба треугольника имеют общий угол E, а основания трапеции, являющиеся параллельными, согласно теореме Фалеса, отсекают на сторонах AE и DE пропорциональные отрезки отрезки, то треугольники EAD и EBC являются подобными. Способ 1. Опустим из вершины E высоту на основание AD. Она же будет высотой для основания BC, поскольку основания трапеции параллельны. Обозначим высоту для треугольника EAD как h₁, а для треугольника EBC как h₂. Таким образом: Площадь треугольника EAD будет равна S_EAD=1/2*AD*h₁. Площадь треугольника EBC будет равна S_EBC=1/2*BC*h₂. Поскольку треугольники подобны, то все стороны относятся друг к другу с одним и тем же коэффициентом подобия. Поскольку основания трапеции относятся дрцг к другу как 5:7, то и все остальные стороны относятся друг к другу с тем же соотношением. Из этого следует: BC / AD = 5 / 7 BC = 5AD / 7 аналогично: h₂ / h₁ = 5 / 7 h₂  = 5h₁ / 7 Таким образом: S_EBC=1/2*BC*h₂. Подставим значения сторон меньшего подобного треугольника через значения сторон большего подобного треугольника: S_EBC=1/2*(5AD / 7)*(5h₁ / 7) S_EBC=1/2*AD*h₁*25 / 49 Заметим, что по условию задачи площадь получившегося треугольника EAD равна 98 сантиметрам, одновременно S_EAD=1/2*AD*h₁. Подставим вместо указанного выражения его значение: S_EBC = 98*25/49 S_EBC = 50 см² Способ 2. Если нам известна теорема: "площади подобных треугольников относятся как квадрат соотношения их сторон", то площади подобных треугольников AED и BEC будут соотноситься как 5² : 7². То есть: S_EBC / S_EAD = 5² / 7² S_EBC / S_EAD = 25 / 49 S_EBC = S_EAD * 25 / 49 Поскольку площадь треугольника EAD известна нам по условию и составляет 98 см² , то S_EBC = 98 * 25 / 49 S_EBC = 50 см² Продолжение решения. Площадь трапеции ABCD равна разности площадей треугольников AED и BEC. Таким образом, площадь трапеции равна 98 - 50 = 48 см². Ответ: 48 см².