Правильная пирамида с треугольником в основании. Тетраэдр

Правильная треугольная пирамида - это пирамида, основанием которой является правильный треугольник, а вершина проецируется в центр основания.

Свойства правильной треугольной пирамиды:

• боковые ребра правильной пирамиды равны

• все боковые грани правильной пирамиды являются равнобедренными треугольниками

• в правильную треугольную пирамиду можно как вписать, так и описать вокруг неё сферу

• если центры вписанной и описанной вокруг правильной треугольной пирамиды, сферы совпадают, то сумма плоских углов при вершине пирамиды равна π (180 градусов) , а каждый из них соответственно равен π / 3  (пи делить на 3 или 60 градусов ).

• площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему

Тетраэдр

Частным случаем правильной треугольной пирамиды является тетраэдр.

Тетраэдр - это правильный многогранник (правильная треугольная пирамида) у которой все грани являются правильными треугольниками.

У тетраэдра:

• Все грани равны

• 4 грани, 4 вершины и 6 ребер

• Все двугранные углы при рёбрах и все трёхгранные углы при вершинах равны

Медиана тетраэдра - это отрезок, соединяющий вершину с точкой пересечения медиан противоположной грани (медиан равностороннего треугольника, противолежащего вершине)

Бимедиана тетраэдра - это отрезок, соединяющий середины скрещивающихся рёбер (соединяющий середины сторон треугольника, являющегося одной из граней тетраэдра)

Высота тетраэдра - это отрезок, соединяющий вершину с точкой противоположной грани и перпендикулярный этой грани (то есть является высотой, проведенной от любой грани, также совпадает с центром описанной окружности).

Тетраэдр обладает следующими свойствами:

• Все медианы и бимедианы тетраэдра пересекаются в одной точке

• Эта точка делит медианы в отношении 3:1, считая от вершины

• Эта точка делит бимедианы пополам

Площадь, объем, высота, радиус вписанной и описанной окружности и другие формулы для тетраэдра

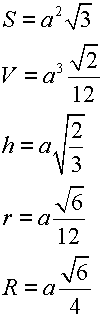
См. пример задачи: формулы и свойства тетраэдра.

Правильная пирамида с треугольником в основании

Примечание. Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме. В задачах вместо символа "квадратный корень" применяется функция sqrt(), в которой sqrt - символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак "√". Задача. Боковая грань правильной треугольной пирамиды представляет собой правильный треугольник, площадь которого 16 корней из 3 см² (16√3). Вычислить периметр основания пирамиды. Решение. Правильный треугольник - это равносторонний треугольник. Соответственно, боковая грань пирамиды представляет собой равносторонний треугольник. Площадь равностороннего треугольника равна: Соответственно: 16√3 = a² √3 / 4 16 = a² / 4 a² = 64 a = 8 см Основанием правильной треугольной пирамиды является правильный (равносторонний) треугольник. Таким образом, периметр основания пирамиды равен 8 * 3 = 24 см Ответ: 24 см. Задача. В правильной треугольной пирамиде высота равна 10 см, а сторона основания 16 см. Найти площадь боковой поверхности. Решение. Поскольку основанием правильной треугольной пирамиды является равносторонний треугольник, то AO является радиусом описанной вокруг основания окружности. (Это следует из свойств правильной пирамиды) Радиус окружности, описанной вокруг равностороннего треугольника найдем из его свойств 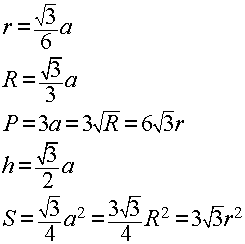Откуда длина ребер правильной треугольной пирамиды будет равна: AM² = MO² + AO² высота пирамиды известна по условию (10 см), AO = 16√3/3 AM² = 100 + 256/3 AM = √(556/3) Каждая из сторон пирамиды представляет собой равнобедренный треугольник. Площадь равнобедренного треугольника найдем как S = 1/2 * 16 sqrt(  (√(556/3) + 8) (√(556/3) - 8) ) S = 8 sqrt(  (556/3) - 64 ) S = 8 sqrt(  364/3 ) S = 16 sqrt(  91/3 ) Поскольку все три грани у правильной пирамиды равны, то площадь боковой поверхности будет равна 3S = 48 √(91/3) Ответ: 48 √(91/3)