Призма с треугольником в основании ( часть 2)

Примечание. Это часть урока с задачами по геометрии (раздел стереометрия, задачи о призме). Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме. В задачах вместо символа "квадратный корень" применяется функция sqrt(), в которой sqrt - символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак "√".

Задача

Площадь боковой поверхности правильной треугольной призмы равна площади основания. Вычислите длину бокового ребра, если сторона основания 7см. Решение. Площадь правильного треугольника, который является основанием правильной треугольной призмы, найдем по формуле: S = a²√3 / 4 S = 49√3 / 4 Площадь боковой поверхности правильной треугольной призмы найдем по формуле S = 3 ab тогда S = 3 * 7 * b = 21b Таким образом, 49√3 / 4 = 21b b = 49√3 / 84 b = 7√3 / 12 Ответ: 7√3 / 12

Задача

В основании прямой треугольной призмы лежит прямоугольный треугольник с катетами 8 и 6 см. Найти боковое ребро призмы, если ее боковая поверхность равна 120 квадратных сантиметров. Решение. Сначала найдем гипотенузу основания призмы. AB² = AC² + BC² AB² = 8² + 6² AB² = 64 + 36 AB = √100 AB = 10 Обозначим боковое ребро призмы как  h . Боковое ребро одновременно является и высотой призмы, поскольку по условию задачи призма является прямой. Тогда площадь боковой поверхности призмы является суммой площадей трех прямоугольников - ACC1A1, CBB1C1 и ABB1A1 или, если подставить известные значения катетов основания призмы, то 10h + 6h + 8h = 120 24h = 120 h =5 Ответ: ребро прямоугольной призмы с прямоугольным треугольником в основании равно 5 см.

Призма с треугольником в основании ( часть 3)

Примечание. Это часть урока с задачами по геометрии (раздел стереометрия, задачи о призме). Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме. В задачах вместо символа "квадратный корень" применяется функция sqrt(), в которой sqrt - символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак "√". Задача. Основание прямой призмы - треугольник со сторонами 5 и 3 см и углом 120 градусов между ними. Наибольшая из площадей боковых граней равна 35 см2, найти площадь боковой поверхности. 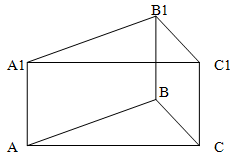Решение. Согласно теореме косинусов Откуда AC² = AB² + BC² - 2*AB*BC*cos 120 AC² = 25 + 9 - 2*5*3*cos 120 Косинус 120 градусов найдем по таблице значений тригонометрических функций. AC² = 34 - 30 (-0.5) AC² = 49 AC = 7 Каждая из граней боковой поверхности представляет собой прямоугольник. При чем длина одной из сторон прямоугольников одинакова и равна высоте призмы. Таким образом, боковая грань призны наибольшей площади лежит на той стороне основания, длина стороны которого наибольшая. То есть наибольшая из боковых граней имеет длину основания 7 см. Откуда высота призмы равна 35 / 7 = 5 см Таким образом, площадь боковой поверхности будет равна сумме площадей каждой из боковых граней S = 5*5 + 3*5 + 7*5 = 75 см² Ответ: 75 см² .