Хорды на окружности

Задача. Хорды АВ и СD пересекаются в точке S, при чем AS:SB = 2:3, DS = 12см, SC = 5см, найти АВ. Решение. 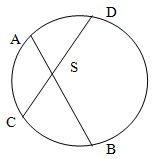Поскольку соотношение AS:SB = 2:3 , то пусть длина AS = 2x, SB = 3x Согласно свойству хорд AS x SB = CS x SD, тогда 2х * 3х = 5 * 12 6х² = 60 х² = 10 x = √10 Откуда AB = AS + SB AB = 2√10 + 3√10= 5√10 Ответ: 5√10 Задача. Окружность разделена на части, которые относятся как 3,5:5,5:3 и точки деления соединены между собой. Определить величину углов образовавшегося треугольника. Решение. Обозначим коэффициент пропорциональности дуг окружности, как х. Соединим центры окружности с концами дуг. Поскольку центральный угол равен градусной мере дуги, на которую опирается, то соотношение центральных углов окружности будет равно соотношению ее частей (дуг). 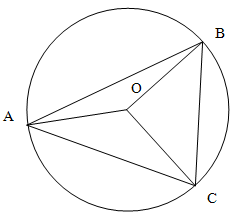Поскольку градусная мера окружности равна 360 градусам, то 3,5х + 5,5х + 3х = 360 12х = 360 х = 30 Откуда градусные величины центральных углов равны: 3 * 30 = 90 3,5 *30 = 105 5,5 *30 = 165 Углы образовавшегося треугольника являются углами, вписанными в окружность. Вписанный угол равен половине градусной меры дуги, на которую опирается. Откуда углы треугольника равны: 90 / 2 = 45 105 / 2 = 52,5 165 / 2 = 82,5 Ответ: Величина углов треугольника равна 45 ; 52,5 ; 82,5 ;

Треугольники

Задачи по геометрии про треугольники и их свойства. Рассматриваются задачи по геометрии, решение которых вызывает у школьников трудности. Основное внимание уделяется принципу решения подобных задач.

Высота Задача на подобие треугольников.

В прямоугольном треугольнике ABC (угол C = 90⁰) проведена высота CD. Определите CD, если AD = 9 см, BD = 16 см

Решение.

Треугольники ABC, ACD и CBD подобны между собой . Это непосредственно следует из второго признака подобия (равенство углов в этих треугольниках очевидно).

Прямоугольные треугольники - единственный вид треугольников, которые можно разрезать на два треугольника, подобных между собой и исходному треугольнику.

Обозначения этих трех треугольников в таком порядке следования вершин: ABC, ACD, CBD. Тем самым мы одновременно показываем и соответствие вершин. (Вершине A треугольника ABC соответствует также вершина A треугольника ACD и вершина C треугольника CBD и т. д.)

Треугольники ABC и CBD подобны. Значит:

AD/DC = DC/BD, то есть

DC²=AD*BD

DC²=9*16

DC=12 см

Задача на применение теоремы Пифагора.

Треугольник ABC является прямоугольным. При этом C-прямой угол. Из него проведена высота CD=6см.  Разность отрезков BD-AD=5 см.

Найти: Стороны треугольника ABC. Решение.

1.Составим систему уравнений согласно теореме Пифагора

CD²+BD²=BC²

CD²+AD²=AC²

поскольку CD=6

36+BD²=BC²

36+AD²=AC²

Поскольку BD-AD=5, то

BD = AD+5, тогда система уравнений принимает вид

36+(AD+5)²=BC²

36+AD²=AC²

Сложим первое и второе уравнение. Поскольку левая часть прибавляется к левой, а правая часть к правой - равенство не будет нарушено. Получим:

36+36+(AD+5)²+AD²=AC²+BC²

72+(AD+5)²+AD²=AC²+BC²

2. Теперь, взглянув на первоначальный чертеж треугольника, по той же самой теореме Пифагора, должно выполняться равенство:

AC²+BC²=AB²

Поскольку AB=BD+AD, уравнение примет вид:

AC²+BC²=(AD+BD)²

Поскольку BD-AD=5, то BD = AD+5, тогда

AC²+BC²=(AD+AD+5)²

3. Теперь взглянем на результаты, полученные нами при решении в первой и второй части решения. А именно:

72+(AD+5)²+AD²=AC²+BC²

AC²+BC²=(AD+AD+5)²

Они имеют общую часть AC²+BC² . Таким образом, приравняем их друг к другу.

72+(AD+5)²+AD²=(AD+AD+5)²

72+AD²+10AD+25+AD²=4AD²+20AD+25

-2AD²-10AD+72=0

В полученном квадратном уравнении дискриминант равен D=676, соответственно, корни уравнения равны:

х₁=-3,5

x₂=4 

Поскольку длина отрезка не может быть отрицательной, отбрасываем первый корень.

AD=4

Соответственно

BD = AD + 5 = 9

AB = BD + AD = 4 + 9 = 13

По теореме Пифагора находим остальные стороны треугольника:

AC = корень из (52)

BC = корень из (117).