Параллелограмм

Примечание. Это часть урока с задачами по геометрии (раздел параллелограмм). Здесь размещены задачи, которые вызывают трудности при решении. Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме. Для обозначения действия извлечения квадратного корня в решениях задач используется символ √  или sqrt(), при чем в скобках указано подкоренное выражение. Задача. Высоты параллелограмма равны 5см и 4см, а периметр равен 42см. Найдите площадь параллелограмма. Решение. Площадь параллелограмма равна произведению стороны на высоту, опущенную на эту сторону.  Обозначим стороны параллелограмма как a и b. Следовательно площадь и периметр будут равны: S = 4a S = 5b P = 2a + 2b Откуда 4a = 5b a = 5/4b Поскольку периметр параллелограмма равен 42 см, то 2( 5/4b ) + 2b = 42 b = 9 1/3 Откуда a = 11 2/3 Теперь находим площадь параллелограмма: S = 4 * 11 2/3 = 5 * 9 1/3 = 46 2/3 см² . Ответ: 46 2/3 см² . Задача. Периметр параллелограмма равен 16 см. Чему равны стороны параллелограмма, если известно, что одна его сторона в 3 раза больше другой Решение. У параллелограмма противоположные стороны равны, обозначим их как а и b, тогда периметр будет равен: Р = 2(а+b). Пусть х - это сторона а, тогда b=3х. 2(х+3х)=16 2*4х=16 х=2 значит сторона а=2, а сторона b=6. Ответ: 2 и 6.

Параллелограмм (часть 2) Задача

На диагонали МР прямоугольника МNРQ отложены равные отрезки МА и РВ. Докажите, что АNBQ параллелограмм. Решение. Четырехугольник является параллелограммом, если его противоположные стороны попарно равны. Докажем это. Исходя из условия задачи треугольники MAN и PBQ равны. Так как PB = AM по условию задачи, PQ = NM как противоположные стороны прямоугольника, а углы BPQ и NMA равны, как внутренние накрест лежащие для параллельных прямых NP и MQ и секущей MP. Аналогично доказывается равенство треугольников NBP и QAM. Поскольку описанные треугольники равны, то NA = BQ,  NB = BQ. Таким образом, поскольку противолежащие стороны равны, то АNBQ параллелограмм.

Задача

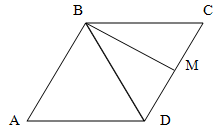
В параллелограмме ABCD диагональ BD = 6 см и образует со сторонами AD и DC углы по 60 градусов. Определите углы и периметр параллелограмма ABCD. Дополнительно: определите вид четырехугольника ABMD, где точка M - середина DC, определите углы четырехугольника ABMD. Решение. Поскольку нам дана величина угла ADB (диагональ параллелограмма образует со сторонами AD и DC углы по 60 градусов), то величина угла DBC также равна 60 градусов, поскольку противоположные стороны параллелограмма параллельны, соответственно диагональ является секущей для двух параллельных прямых AD и BC, а для любой секущей внутренние накрест лежащие углы равны. Таким образом, в треугольнике BCD нам известны два угла из трех, и они оба равны 60 градусов. Соответственно, поскольку сумма углов треугольника равна 180 градусов, то угол BCD также равен 60 градусам, из чего следует, что треугольник BCD - равносторонний. Поскольку треугольник BCD - равносторонний, то BC = CD = BD = 6 см. Таким образом, поскольку противолежащие стороны параллелограмма равны, периметр его равен 24 см. Параллелограмм является ромбом. Дополнительно: Поскольку точка М лежит на стороне CD, то AB и MD - параллельны, следовательно, ABMD - трапеция. Угол DAB трапеции равен 60 градусов, исходя из решения, изложенного выше, как угол параллелограмма. Угол ADM равен 120 градусов, так как по условию диагональ BD образует со сторонами AD и DC углы по 60 градусов, а ADM равен сумме данных углов. Поскольку по условию точка M - середина DC, CM = MD. Значит BM - медиана треугольника DBC. Как указано выше, треугольник DBC - равносторонний, а в равностороннем треугольнике медиана является, одновременно, биссектрисой и высотой. Значит, угол DBM равен половине угла DBC и равен 60 / 2 = 30 градусов. Откуда угол ABM = 60 + 30 = 90 градусов. Поскольку BM - высота, то BMD равен также 90 градусов. Исходя из сказанного,  ABMD - прямоугольная трапеция. Ответ: 24 см. 60º, 90º, 90º, 120º - прямоугольная трапеция.