Окружность, описанная вокруг треугольника

Для нахождения радиуса окружности, описанной вокруг треугольника, можно воспользоваться следующими формулами:

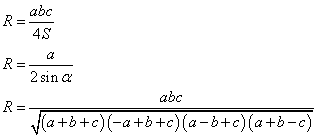
где: a,b,c - стороны треугольника S - площадь треугольника α  - угол, противолежащий стороне a

Окружность, описанная вокруг треугольника

Примечание. В данном уроке изложены задачи по геометрии о треугольниках, вписанных в окружность. Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме.

Задача

Внутри окружности проведены хорды AB и BC, длина которых равна радиусу окружности. Определите величину угла ABC. Решение. Проведем к центру окружности, который обозначим буквой O, отрезки AO, BO и CO. Поскольку по условию задачи AB и BC равны радиусу окружности, а AO, BO и CO равны радиусу по определению, то в треугольнике ABO  AB=AO=BO=r (радиусу окружности), а в треугольнике BCO BC=OC=OB=r (радиусу окружности). Таким образом, треугольники ABO и BCO - равносторонние. Углы равностороннего треугольника равны между собой и составляют 60 градусов. Таким образом углы ABO=OBC=60⁰, а угол ABC равен сумме углов ABO и OBC, ABC = ABO + OBC = 60⁰ + 60⁰= 120⁰. Ответ: Искомый угол ABC, образованный двумя хордами AB и BC равен 120 градусов.

Задача

Гипотенуза прямоугольного треугольника равна 26 см. Найдите радиус описанной окружности. Решение. Центр описанной вокруг прямоугольного треугольника окружности лежит на середине гипотенузы. Значит R = 26/2 = 13 см. Ответ: 13 см.

Задача

В треугольнике АВС угол В=60 градусов, АВ больше ВС на 1, радиус описанной окружности равен √7. Найдите площадь треугольника и длину стороны АС. Решение. обозначим BC как x, тогда AB = x+1 Радиус окружности, описанной вокруг треугольника равен R = a / 2sinα где a - сторона, противолежащая углу α Таким образом, учитывая, что sin 60 градусов равен √3/2 : √7 = AC / 2sin60º √7 = AC / ( 2 √3/2 ) √7 = AC / √3 AC = √21

Окружность, описанная вокруг треугольника (часть 2)

Примечание. Это часть урока с задачами по геометрии (раздел окружность, описанная вокруг треугольника, треугольник, вписанный в окружность). Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме. Для обозначения действия извлечения квадратного корня в решениях задач используется символ √  или sqrt(), при чем в скобках указано подкоренное выражение. Задача. Радиус окружности , описанной около остроугольного треугольника ABC, равен √3 см. Найдите градусную меру угла B , если AC =√6 см Решение. Радиус окружности, описанной вокруг треугольника равен R = a / 2sinα, где a - сторона треугольника, вписанного в окружность, α - противолежащий угол. Таким образом: √3 = √6 / 2sinα 2sinα = √2 sinα = √2/2 Смотрим таблицу значений тригонометрических функций, α = 45º Ответ: градусная мера угла треугольника, вписанного в заданную окружность равна 45 градусов.

Вписанная в треугольник окружность

Свойства вписанной окружности

• В каждый треугольник можно вписать окружность, при этом только одну

• Центр вписанной окружности называется инцентром, он равноудалён от всех сторон

• Центр вписанной окружности является точкой пересечения биссектрис треугольника

Радиус вписанной окружности

Радиус вписанной в произвольный треугольник окружности равен отношению его площади к полупериметру. Формулы радиуса вписанной окружности:

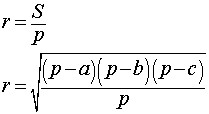
Центр вписанной в треугольник окружности - это точка пересечения биссектрис его улов. При этом стоит заметить, что для равнобедренного треугольника - биссектриса угла напротив основания - является одновременно и высотой.

Четырехугольники

Свойства четырехугольников

Четырехугольник, описанный вокруг окружности (окружность, вписанная в четырехугольник).

Главное свойство описанного четырехугольника:

Четырехугольник можно описать вокруг окружности тогда и только тогда, когда суммы длин противоположных сторон равны.

Четырехугольник, вписанный в окружность (окружность, описанная вокруг четырехугольника)

Главное свойство вписанного четырехугольника:

Четырехугольник можно вписать в окружность тогда и только тогда, когда суммы противоположных углов равны 180 градусов.