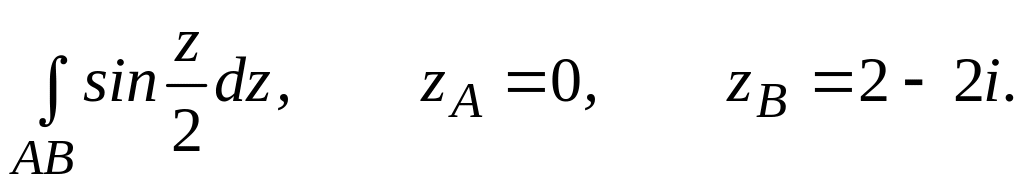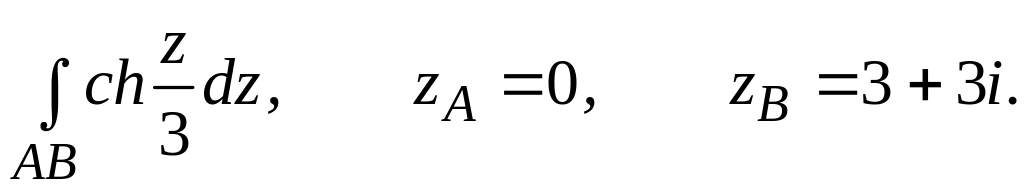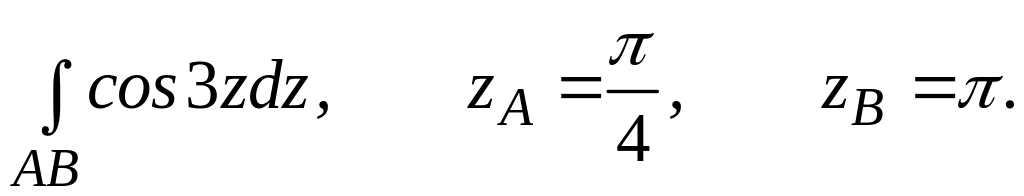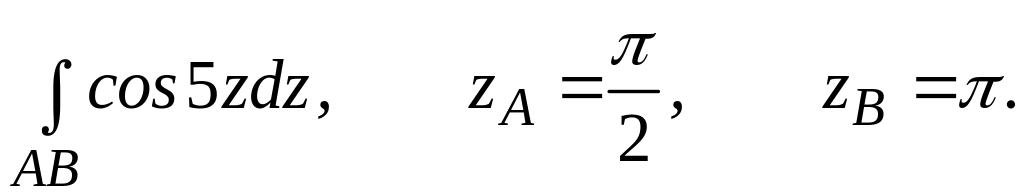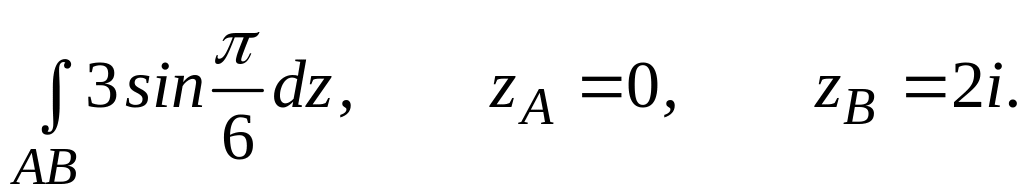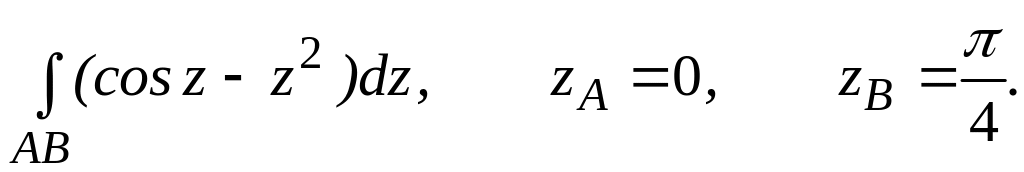4 Завдання для типових розрахунків
4.1 Комплексні числа
4.1.1 Знайти всі корені рівняння і зобразити їх на комплексній площині.
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]()
6. ![]()
7. ![]()
8. ![]()
9. ![]()
10. ![]()
11. ![]()
12. ![]()
13. ![]()
14.
15. ![]()
16. ![]()
17. ![]()
18. ![]()
19. ![]()
20. ![]()
21. ![]()
22. ![]()
23. ![]()
24. ![]()
25. ![]()
26. ![]()
27. ![]()
28. ![]()
29. ![]()
30. ![]()
31. ![]()
32. ![]()
33. ![]()
34.
35. ![]()
36. ![]()
37. ![]()
38. ![]()
39. ![]()
40.
41. ![]()
42. ![]()
43. ![]()
44. ![]()
45. ![]()
46. ![]()
47. ![]()
48. ![]()
49. ![]()
50. ![]()
4.1.2 Для заданих чисел
![]() та
та
![]() виконати вказані дії:
виконати вказані дії:
а) знайти значення
![]() ;
;
б) числа та записати в показниковій та тригонометричній формах;
в) для числа знайти всі корені степеня m та зобразити їх на комплексній площині; зробити перевірку одного з коренів;
г) число піднести до степеня k.
1. ![]() ,
,
![]() ,
,
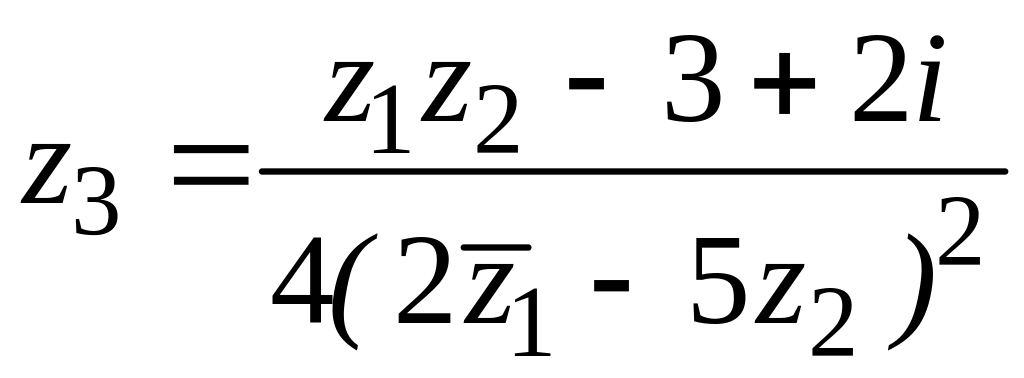 ,
,
![]() ,
,
![]() .
.
2. ![]() ,
,
![]() ,
,
 ,
,
![]() ,
,
![]() .
.
3. ![]() ,
,
![]() ,
,
 ,
,
![]() ,
,
![]() .
.
4. ![]() ,
,
![]() ,
,
 ,
,
,
,
![]() .
.
5. ![]() ,
,
,
,
 ,
,
.
,
,
.
6. ![]() ,
,
![]() ,
,
 ,
,
.
,
,
.
7. ![]() ,
,
![]() ,
,
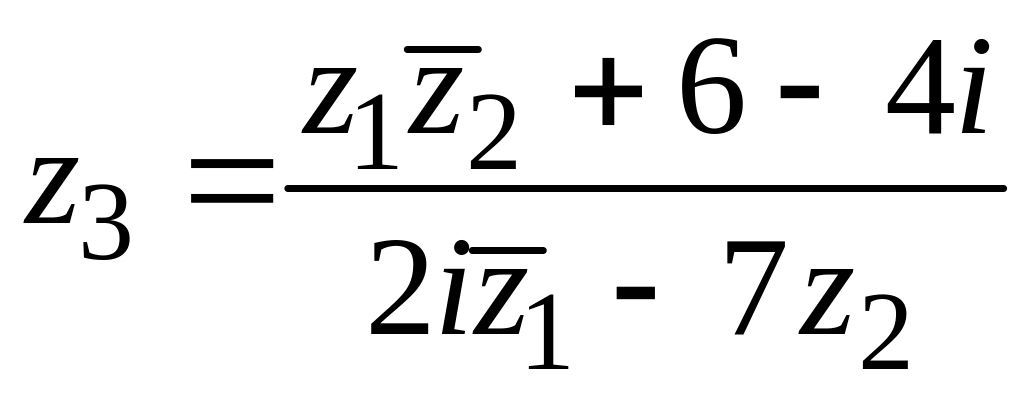 ,
,
.
,
,
.
8. ![]() ,
,
,
,
 ,
,
,
,
![]() .
.
9. ![]() ,
,
![]() ,
,
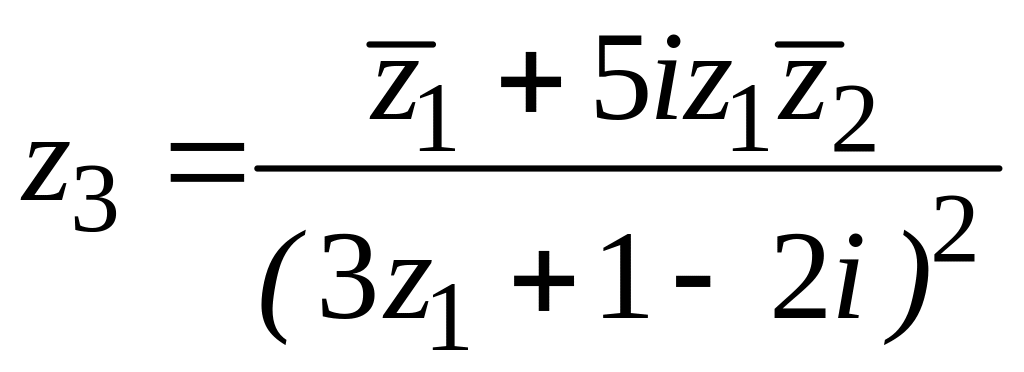 ,
,
.
,
,
.
10. ![]() ,
,
,
,
 ,
,
.
,
,
.
11. , ,
 ,
,
.
,
,
.
12. ![]() ,
,
![]() ,
,
 ,
,
.
,
,
.
13. ![]() ,
,
![]() ,
,
 ,
,
.
,
,
.
14. , ,
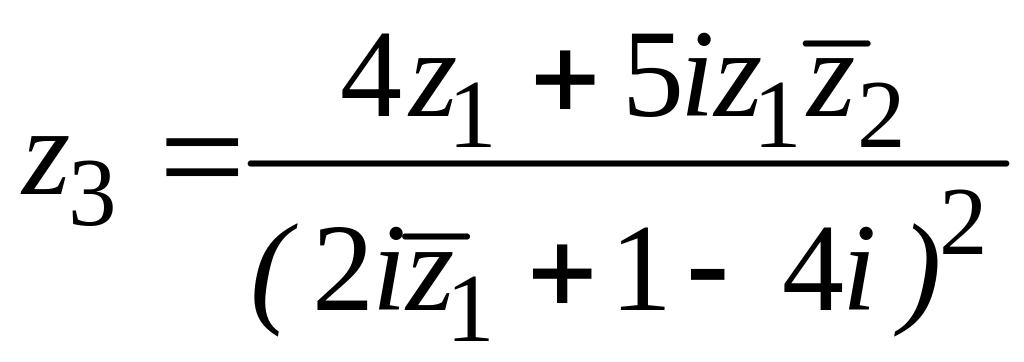 ,
,
.
,
,
.
15. ![]() ,
,
,
,
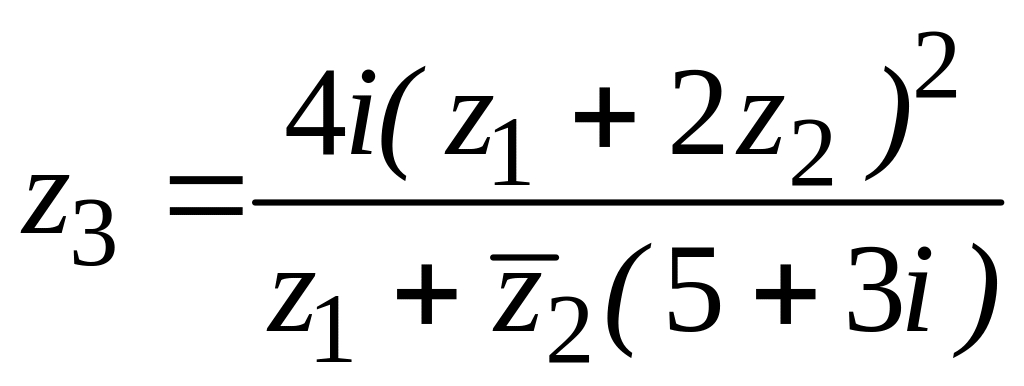 ,
,
.
,
,
.
16.
,
![]() ,
,
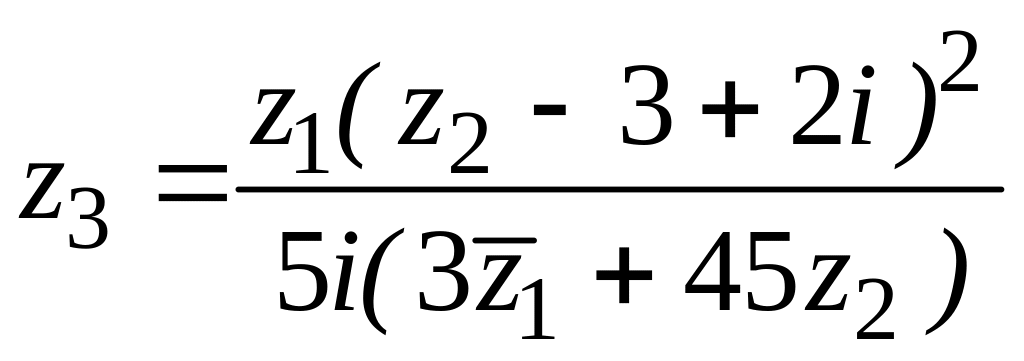 ,
,
.
,
,
.
17. , ,
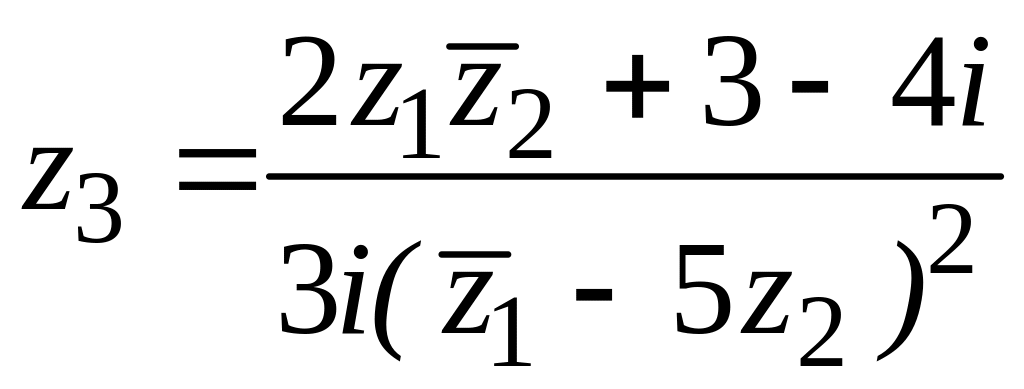 ,
,
.
,
,
.
18. ![]() ,
,
![]() ,
,
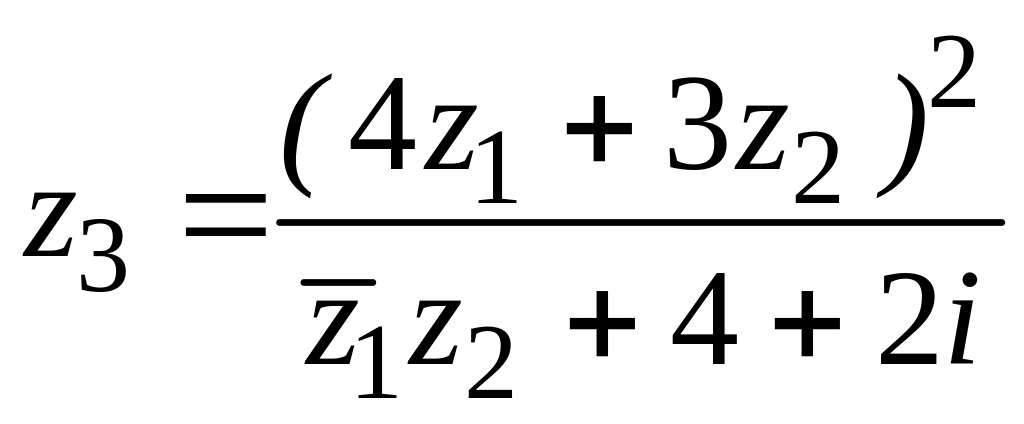 ,
,
.
,
,
.
19. ![]() ,
,
![]() ,
,
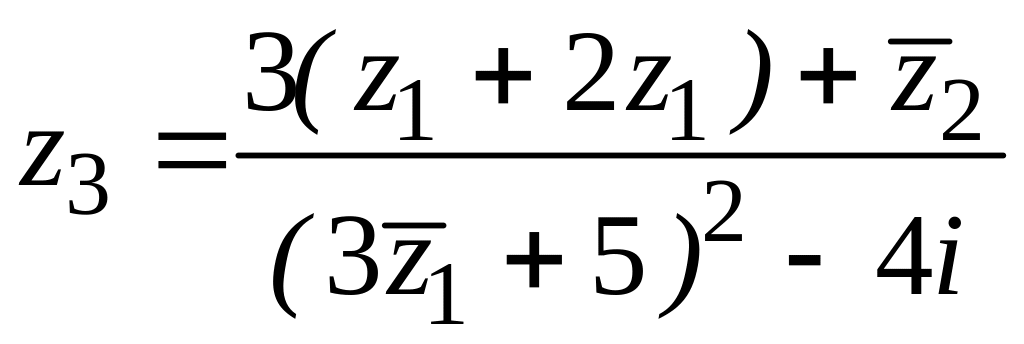 ,
,
.
,
,
.
20. ![]() ,
,
![]() ,
,
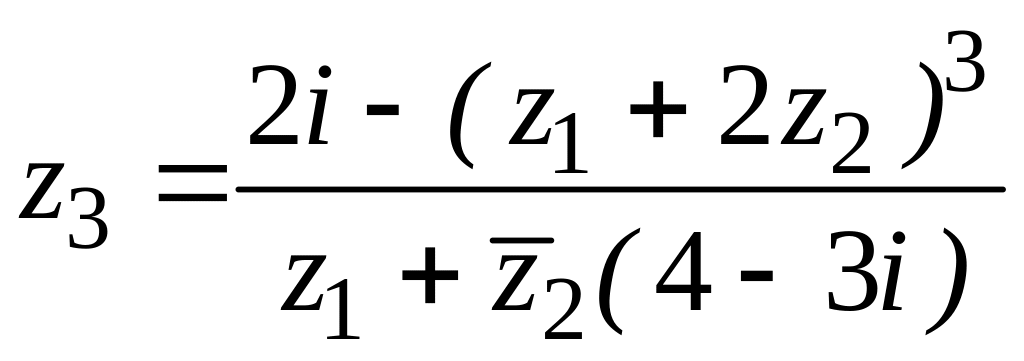 ,
,
.
,
,
.
21.
,
![]() ,
,
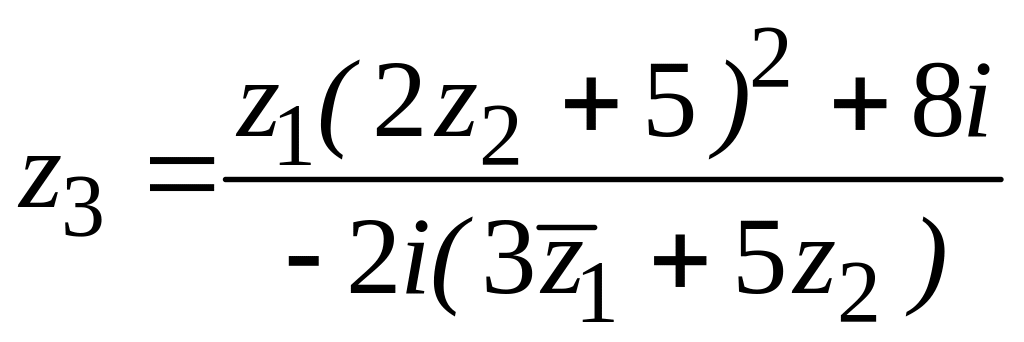 ,
,
.
,
,
.
22.
,
![]() ,
,
 ,
,
.
,
,
.
23. , ,
 ,
,
.
,
,
.
24. ![]() ,
,
,
,
 ,
,
.
,
,
.
25. ![]() ,
,
,
,
 ,
,
.
,
,
.
26. , ,
 ,
,
.
,
,
.
27. , ,
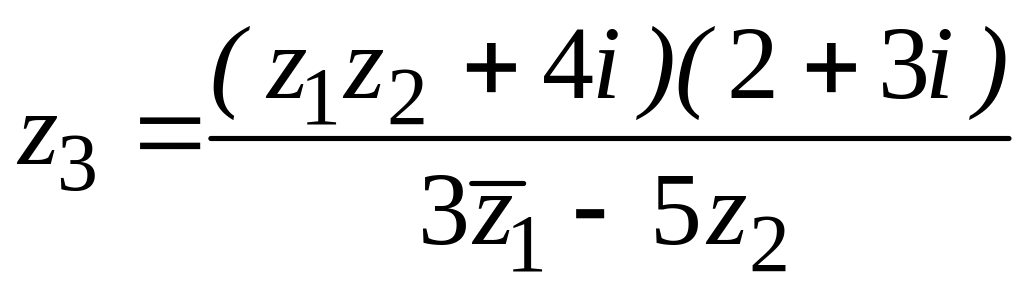 ,
,
.
,
,
.
28. , ,
 ,
,
.
,
,
.
29. ![]() ,
,
![]() ,
,
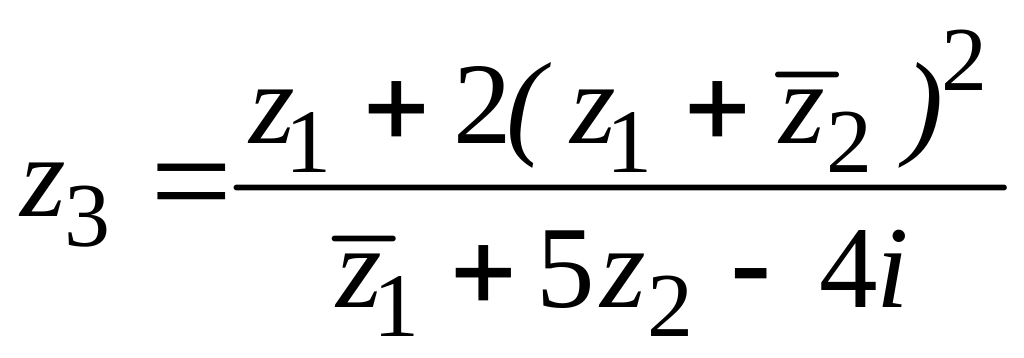 ,
,
.
,
,
.
30.
,
![]() ,
,
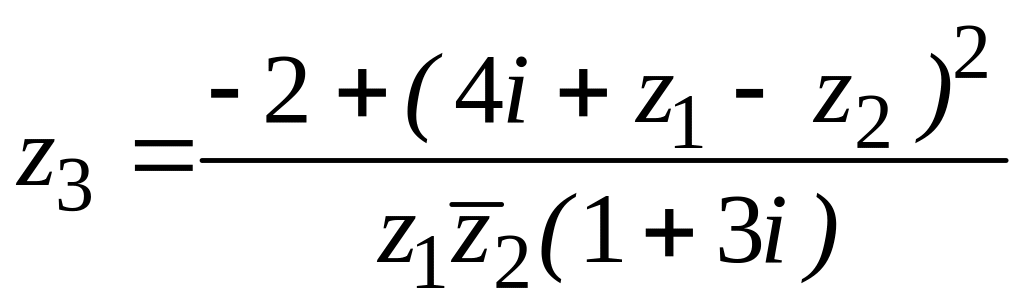 ,
,
.
,
,
.
31.
,
![]() ,
,
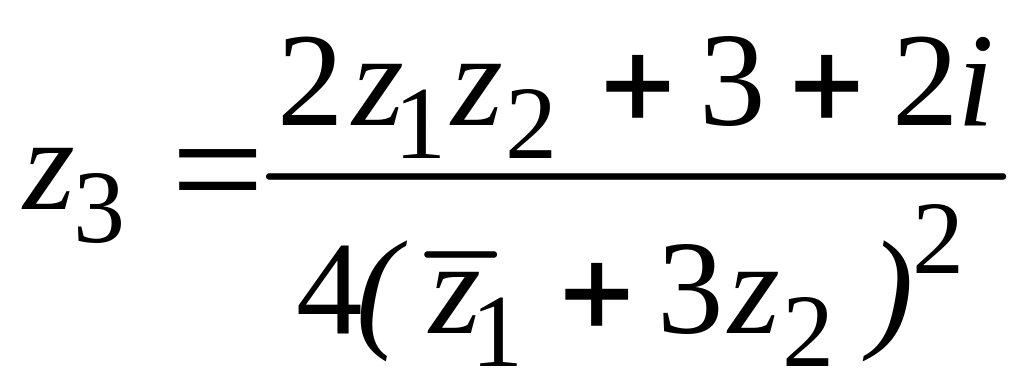 ,
,
.
,
,
.
32. ![]() ,
,
![]() ,
,
 ,
,
.
,
,
.
33. ![]() ,
,
,
,
 ,
,
.
,
,
.
34.
,
![]() ,
,
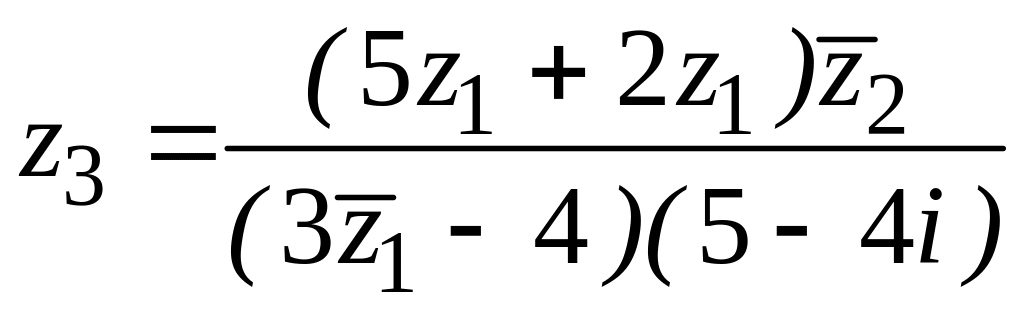 ,
,
.
,
,
.
35. ![]() ,
,
,
,
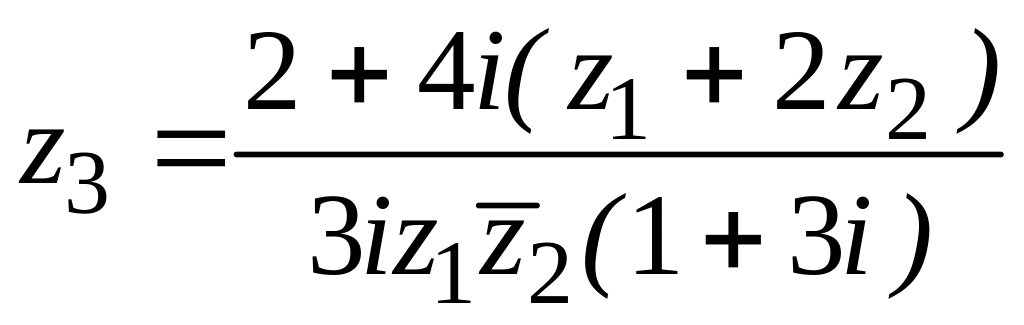 ,
,
.
,
,
.
36. ![]() ,
,
,
,
 ,
,
.
,
,
.
37. ![]() ,
,
,
,
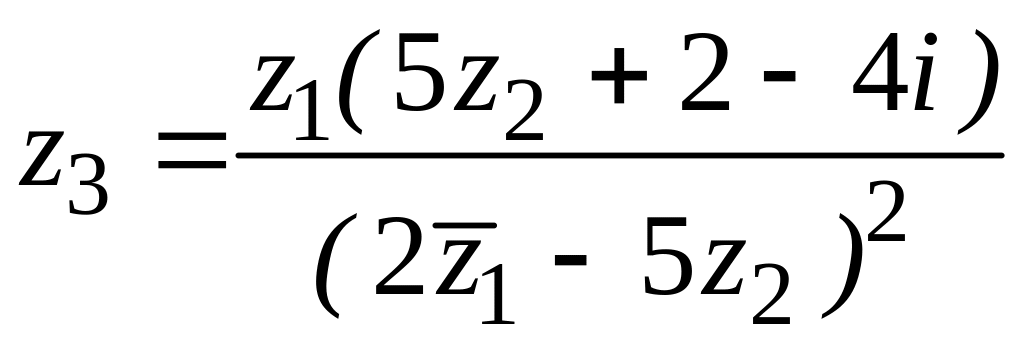 ,
,
.
,
,
.
38.
,
![]() ,
,
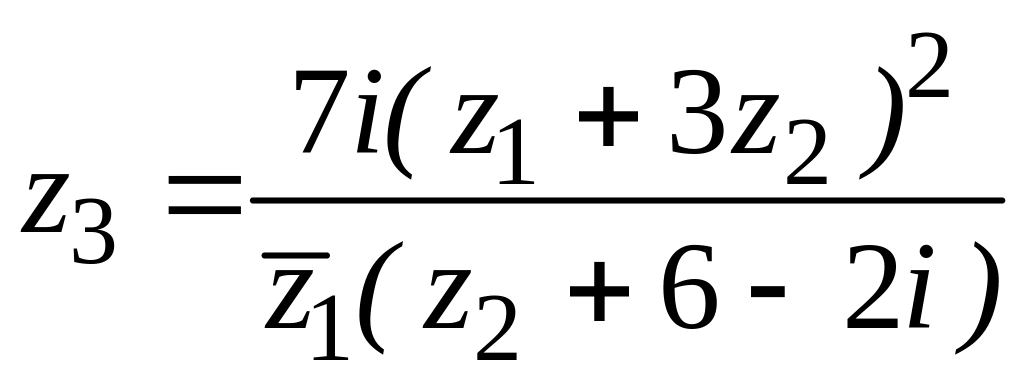 ,
,
,
,
![]() .
.
39. , ,
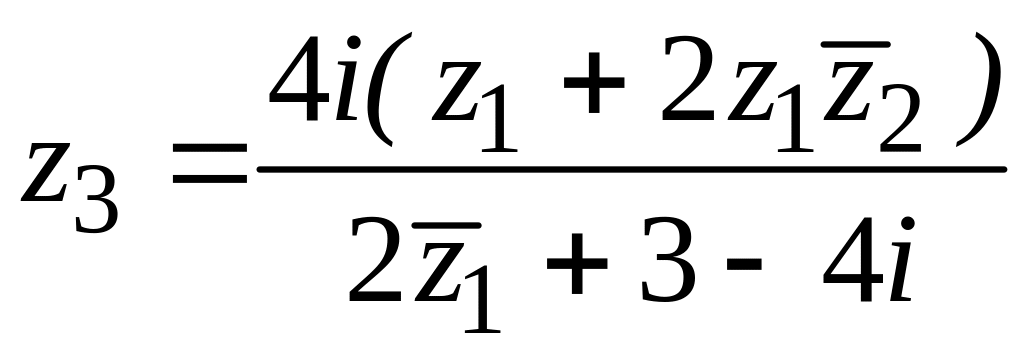 ,
,
.
,
,
.
40. , ,
 ,
,
.
,
,
.
41.
,
![]() ,
,
 ,
,
.
,
,
.
42. , ,
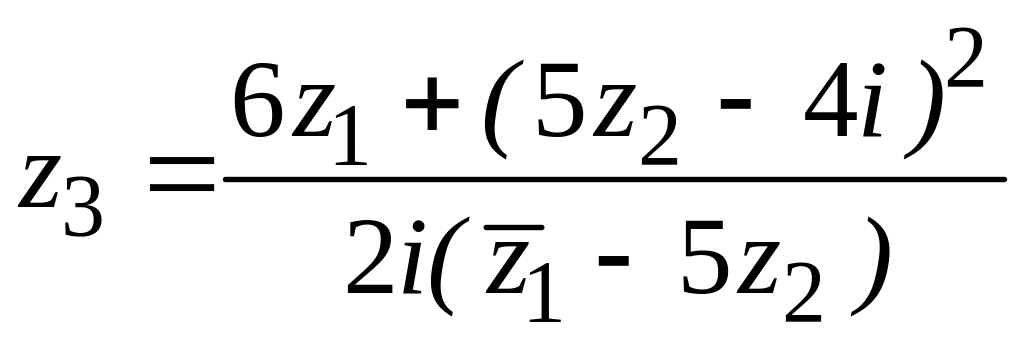 ,
,
.
,
,
.
43.
,
![]() ,
,
 ,
,
.
,
,
.
44. ![]() ,
,
![]() ,
,
 ,
,
.
,
,
.
45. ![]() ,
,
,
,
 ,
,
.
,
,
.
46. , ,
 ,
,
.
,
,
.
47. , ,
 ,
,
.
,
,
.
48. ![]() ,
,
,
,
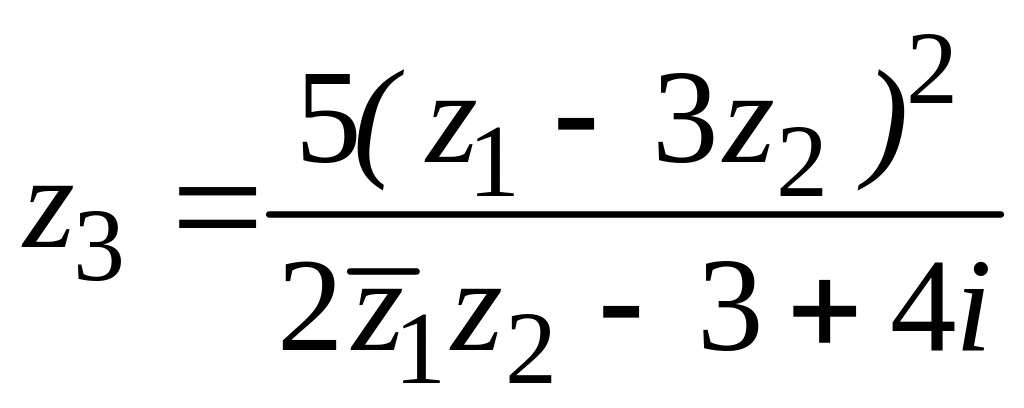 ,
,
.
,
,
.
49. ![]() ,
,
,
,
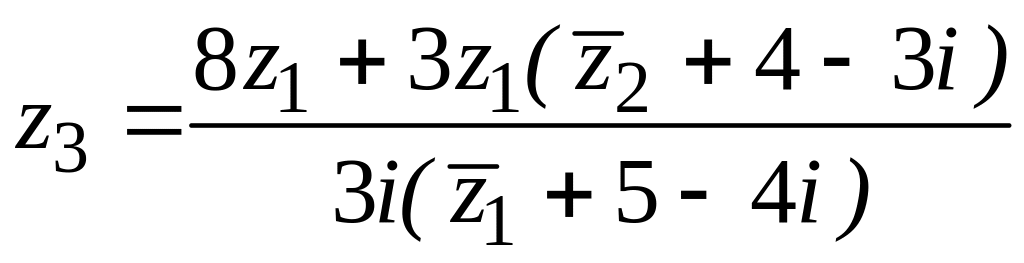 ,
,
.
,
,
.
50. ![]() ,
,
,
,
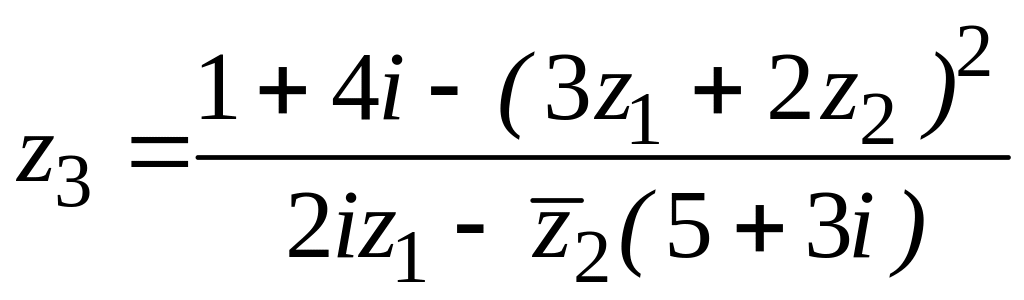 ,
,
.
,
,
.
4.2 Функції комплексної змінної
4.2.1 Зобразити на комплексній площині множини точок, які задовольняють вказані нерівності.
1. ![]() .
.
2. ![]() .
.
3. ![]() .
.
4. ![]()
5. ![]() .
.
6. ![]()
7. ![]() .
.
8. 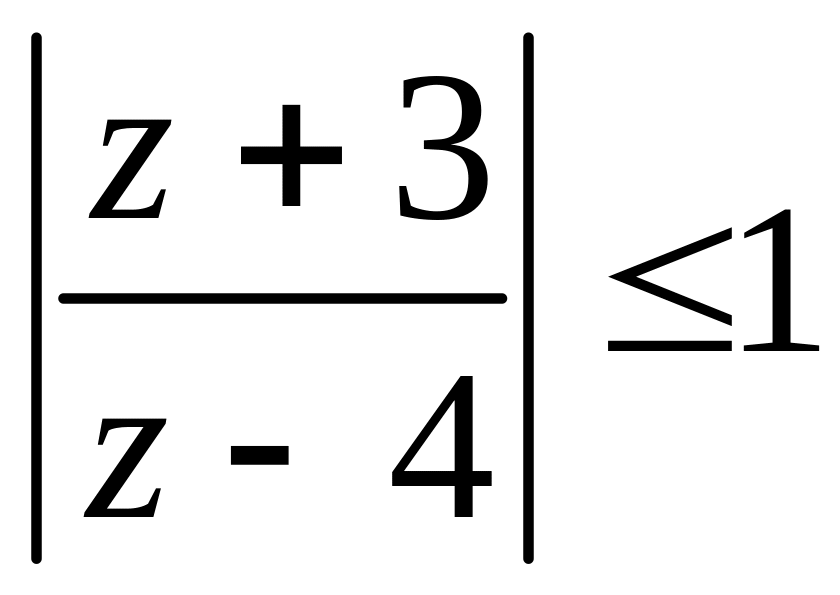 .
.
9. ![]() .
.
10. ![]() .
.
11. ![]() .
.
12. ![]() .
.
13. .
14.  .
.
15. ![]() .
.
16. ![]() .
.
17. ![]() .
.
18. ![]() .
.
19. ![]() .
.
20. ![]() .
.
21. ![]() .
.
22. ![]() .
.
23. .
24. 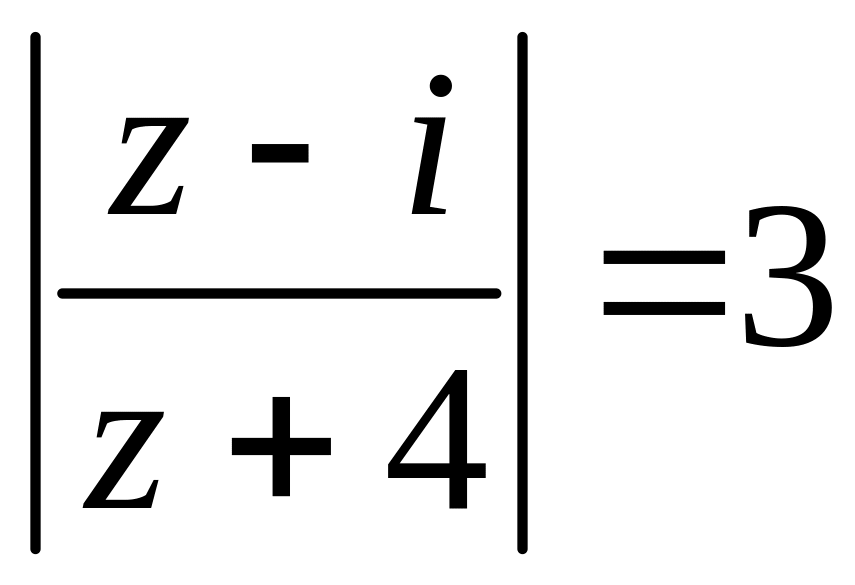 .
.
25. ![]() .
.
26. ![]() .
.
27. ![]() .
.
28. ![]() .
.
29. ![]() .
.
30. ![]() .
.
31. ![]() .
.
32. ![]() .
.
33. ![]() .
.
34. .![]()
35. ![]() .
.
36. ![]()
37. ![]() .
.
38.  .
.
39. ![]() .
.
40. ![]() .
.
41. ![]() .
.
42. ![]() .
.
43. ![]() .
.
44. ![]()
45. ![]() .
.
46. ![]()
47. ![]() .
.
48.  .
.
49. ![]() .
.
50. ![]() .
.
4.2.2 Довести, що функція аналітична на всій комплексній площині. Знайти похідну функції
а) за теоремою Коші-Рімана;
б) за таблицею похідних.
Показати, що значення похідних збігаються.
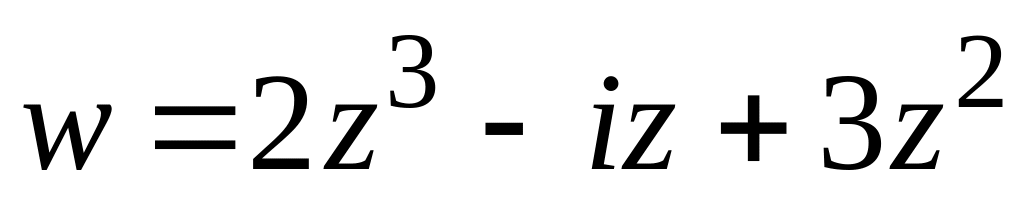 .
.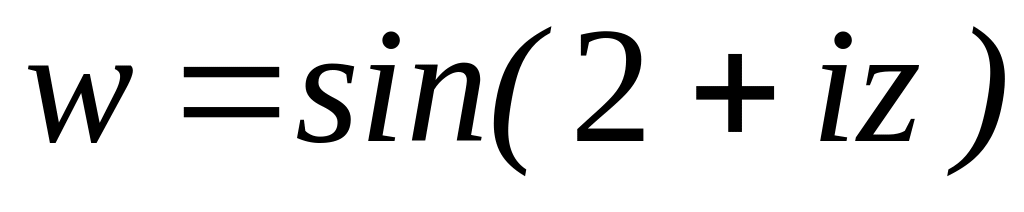
 .
. .
.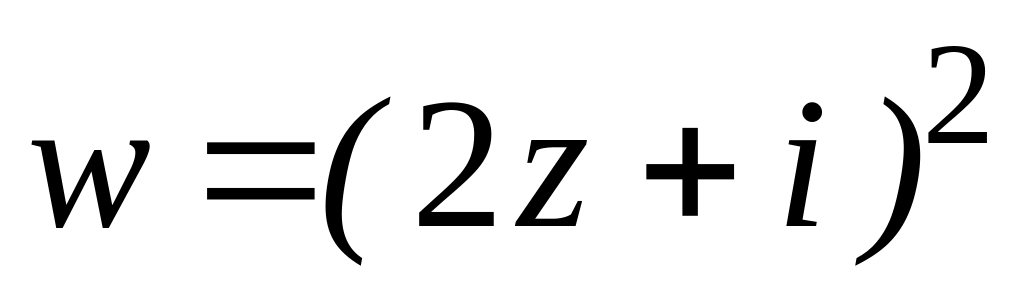
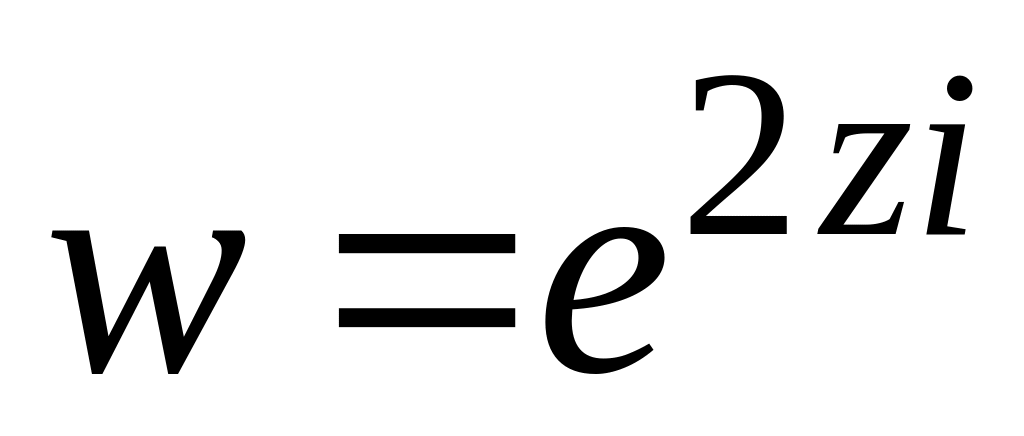 .
.
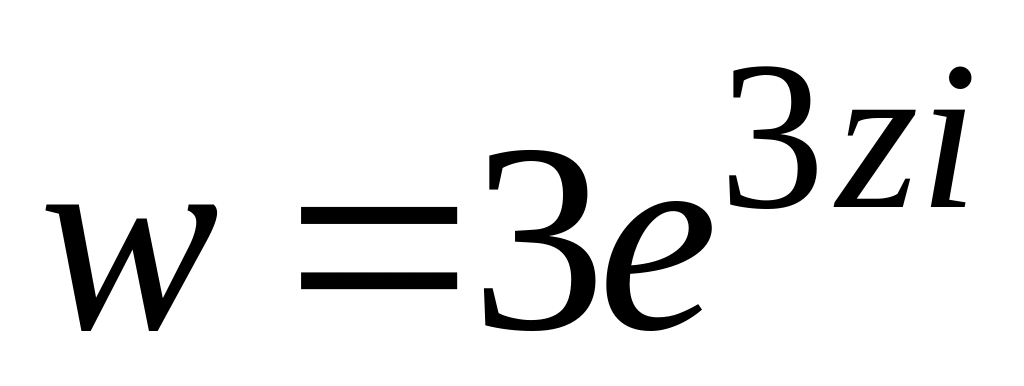 .
.
 .
.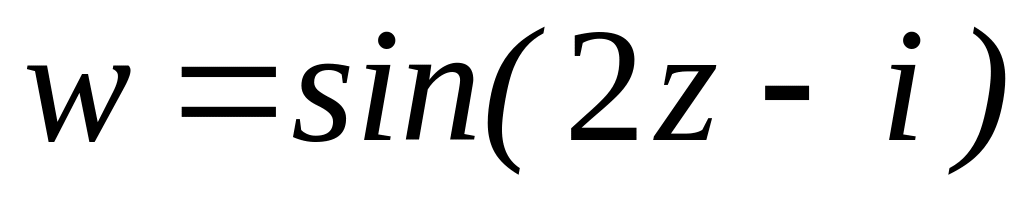 .
. .
. .
. .
. .
.
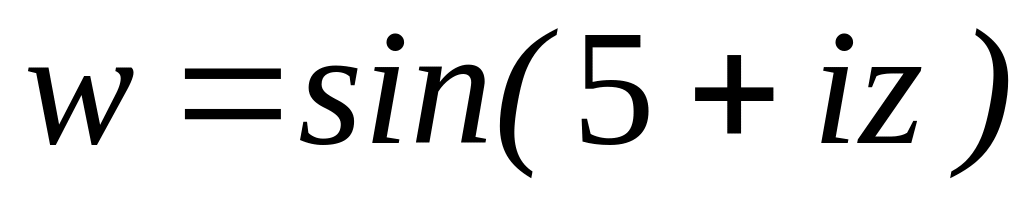
 .
.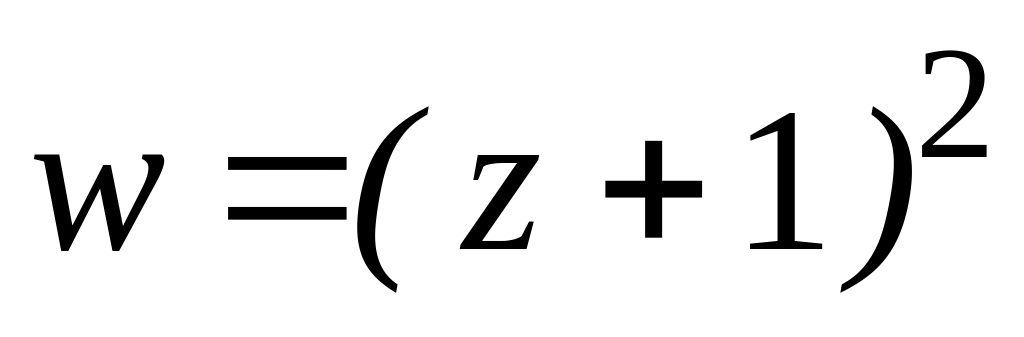 .
.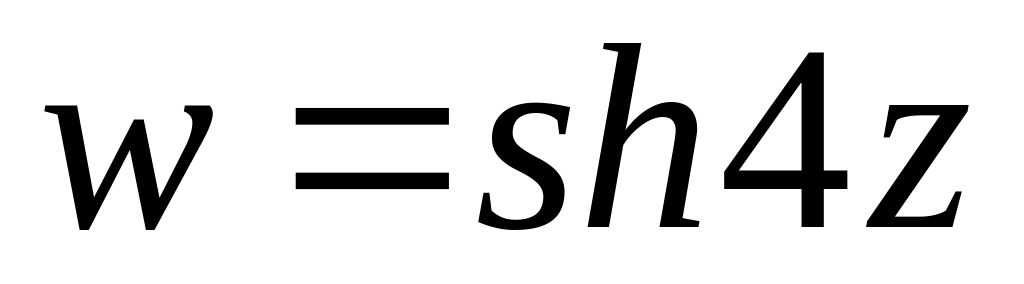
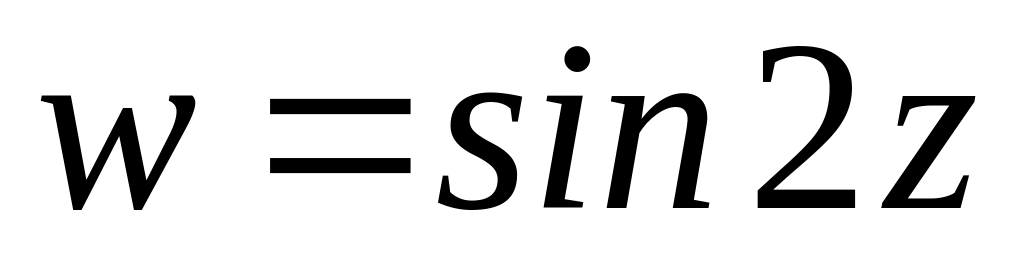 .
..
 .
. .
.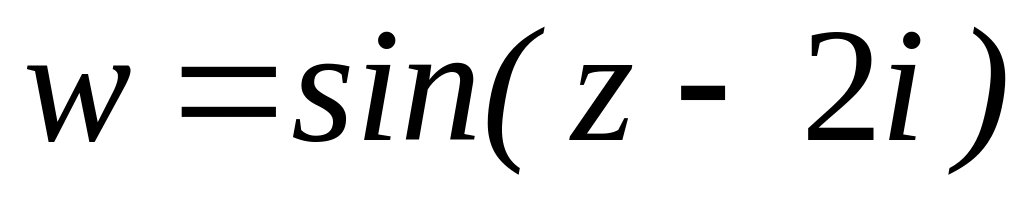 .
. .
. .
. .
.
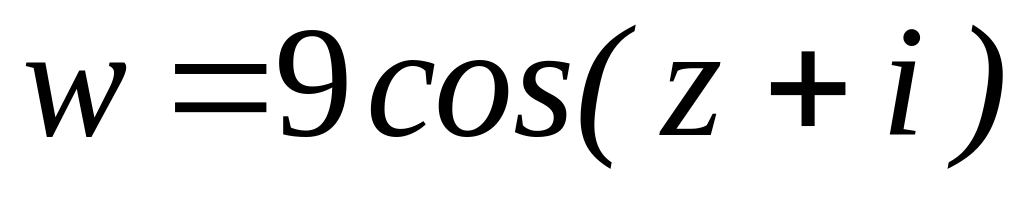 .
.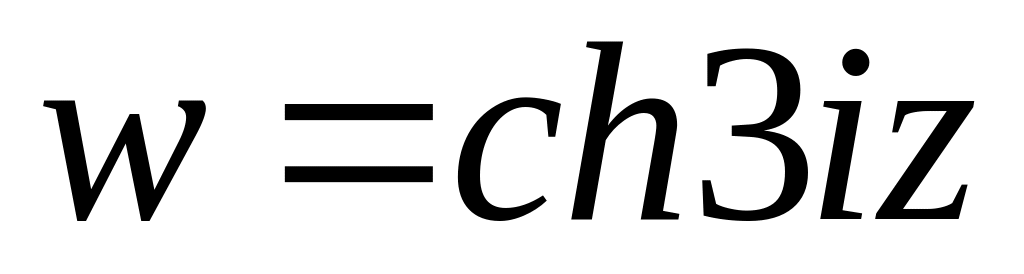
 .
.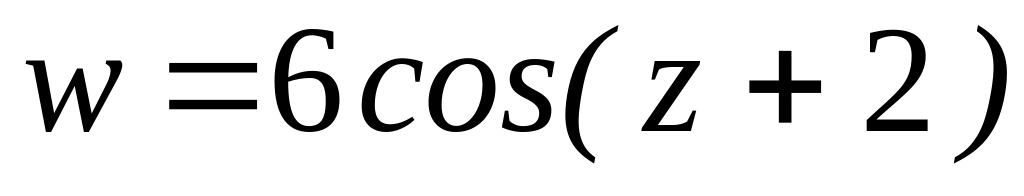 .
.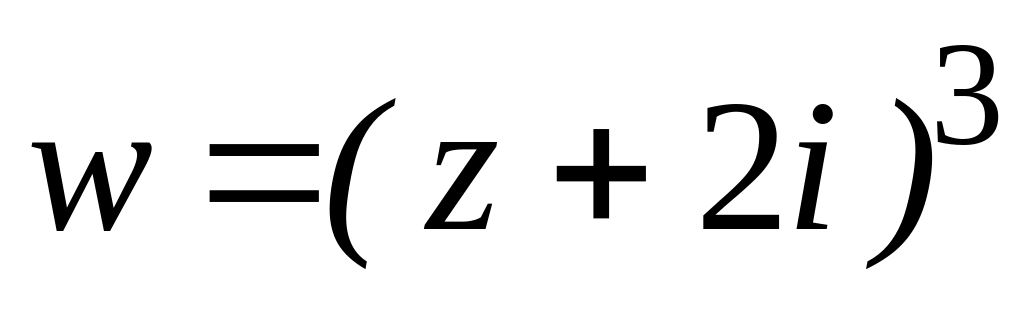
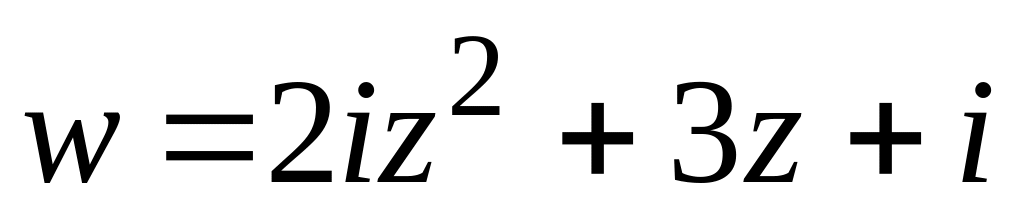
 .
.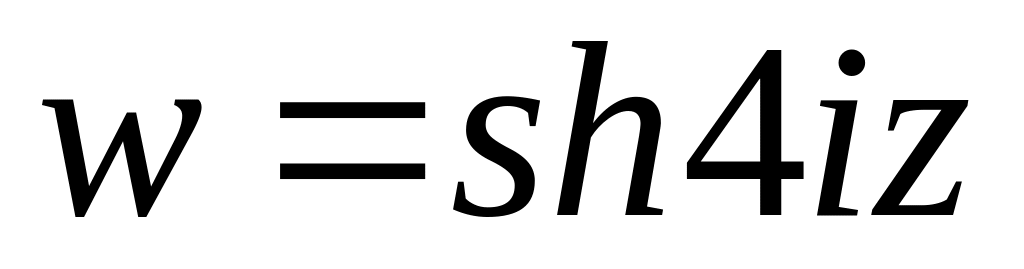 .
.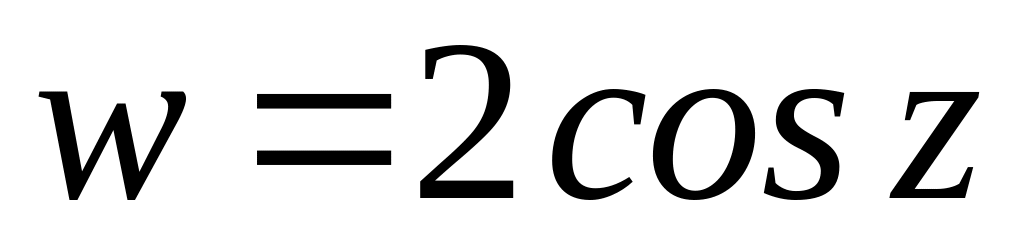 .
. .
.
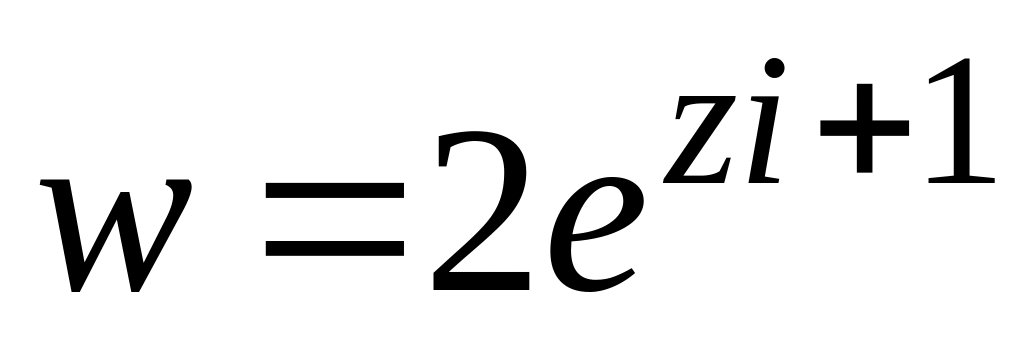 .
.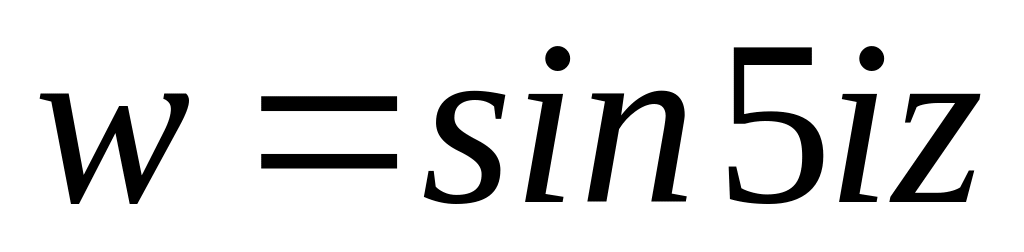
 .
. .
.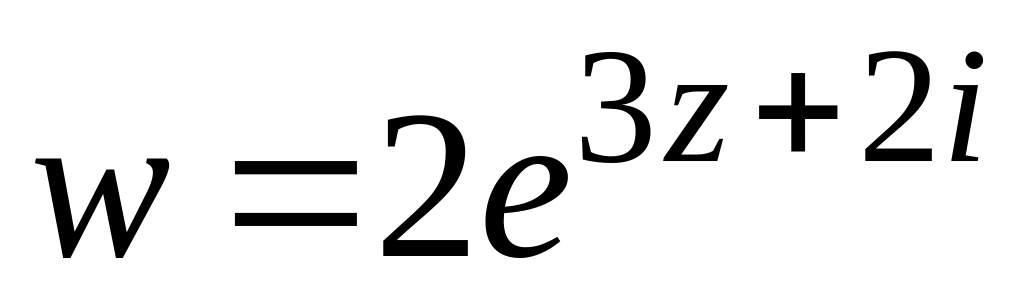 .
.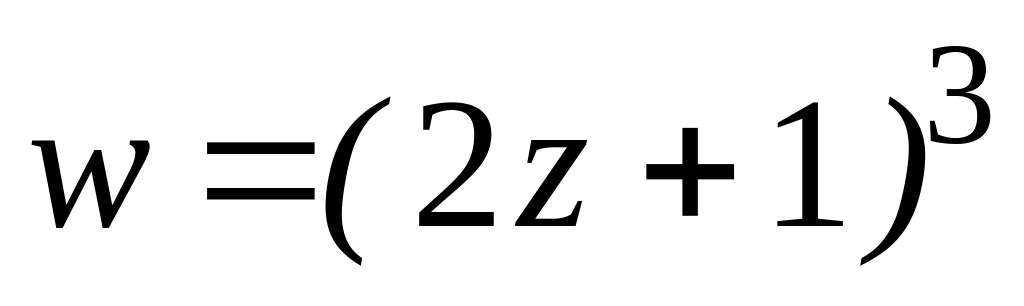
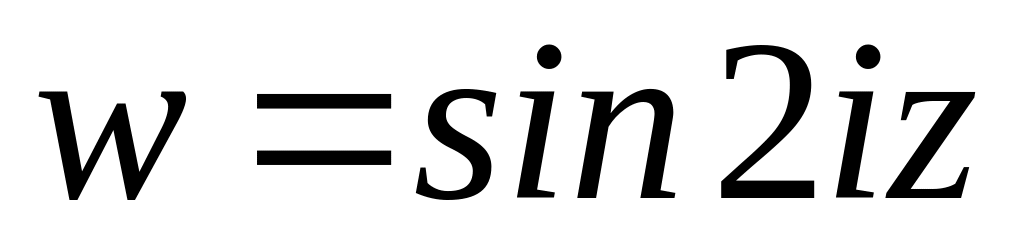 .
..
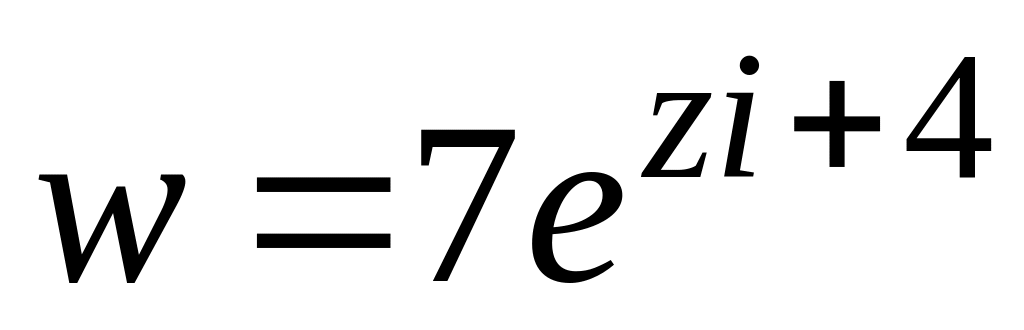 .
.

4.2.3 Відновити аналітичну в околі
![]() функцію
функцію
![]() за заданою дійсною
за заданою дійсною
![]() чи уявною
чи уявною
![]() частиною.
частиною.
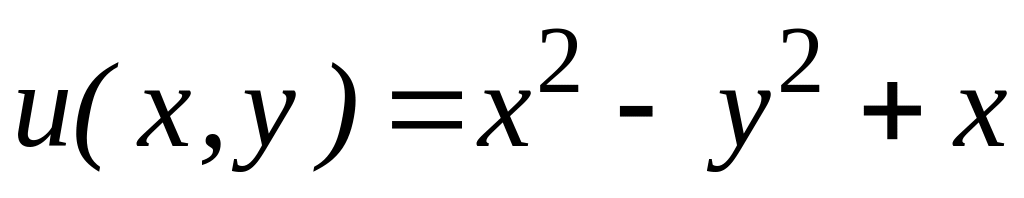 ,
, 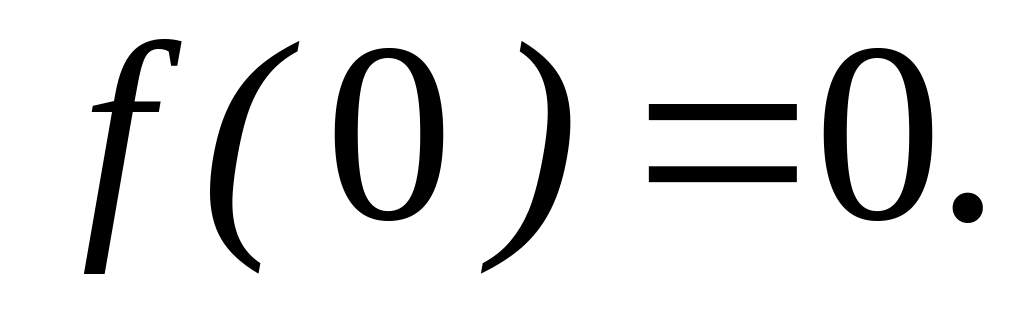
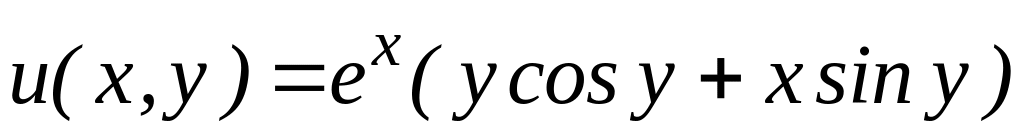 ,
,

 ,
, 
 ,
, 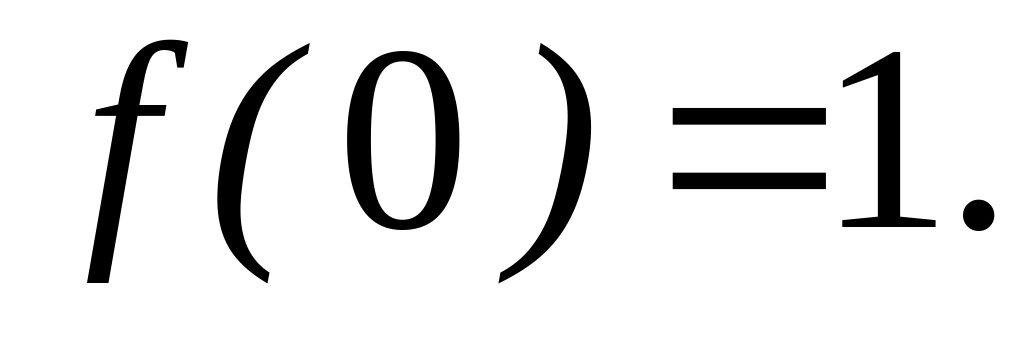
 ,
,
 ,
, 

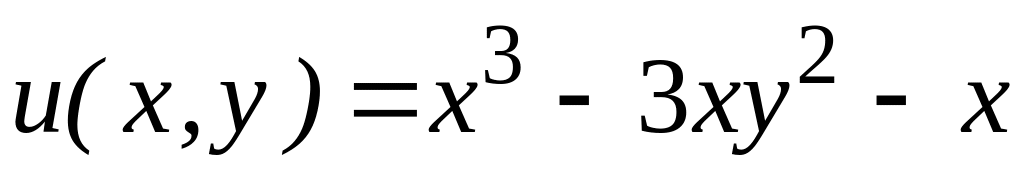 ,
,
 ,
,
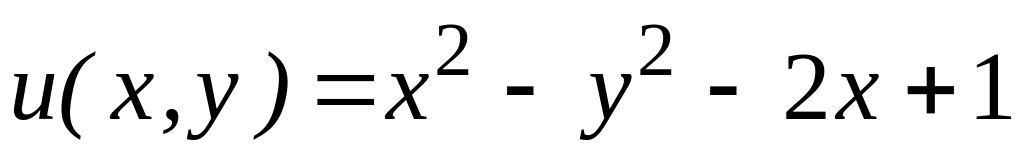 ,
,
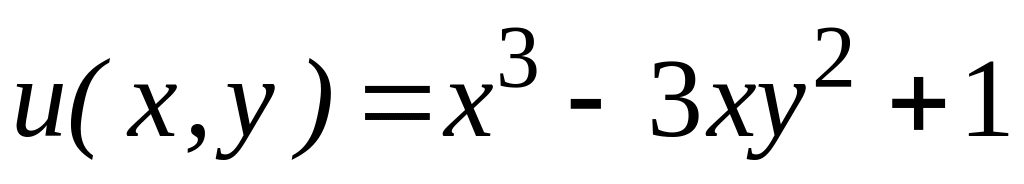 ,
,
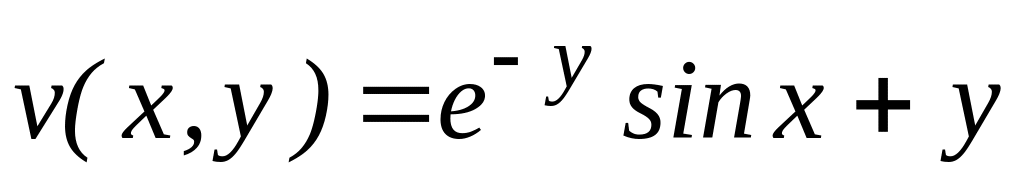 ,
,
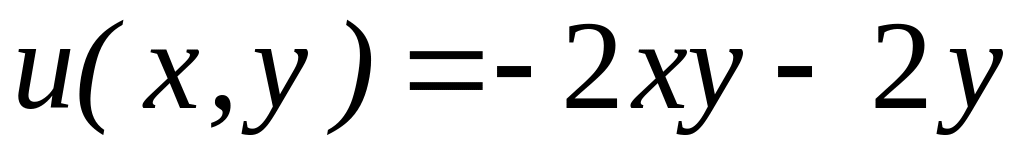 ,
, 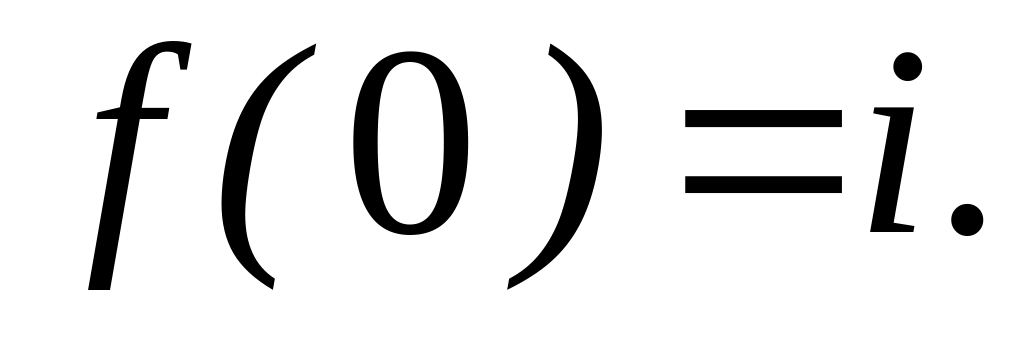
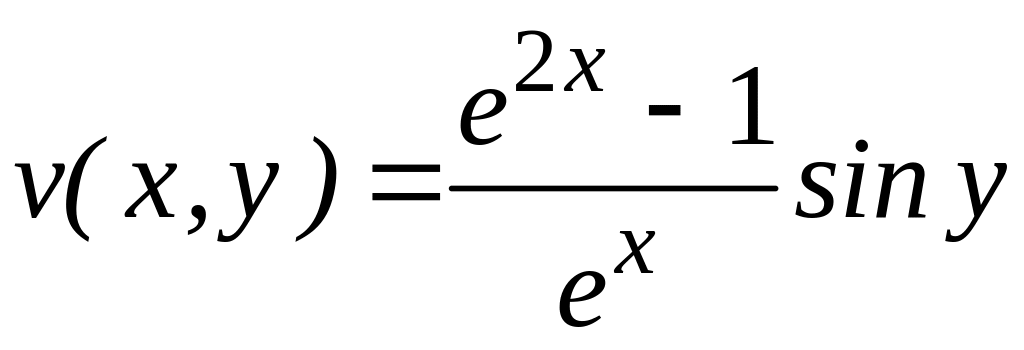 ,
,
 ,
,
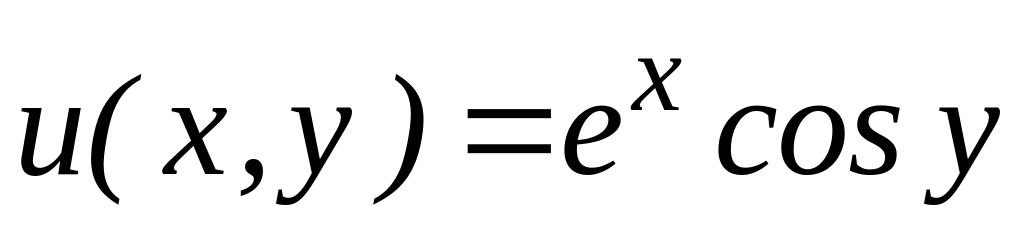 ,
,
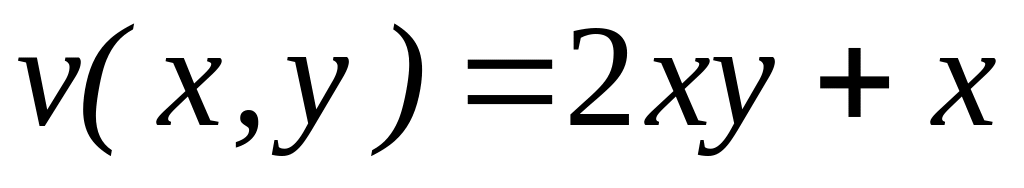 ,
,
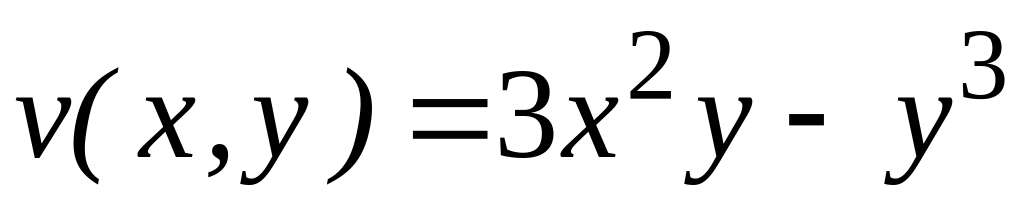 ,
,
 ,
,
 ,
,
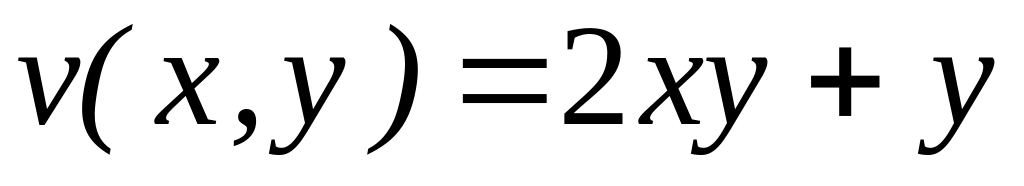 ,
,
 ,
,
 ,
,
 ,
,

 ,
,
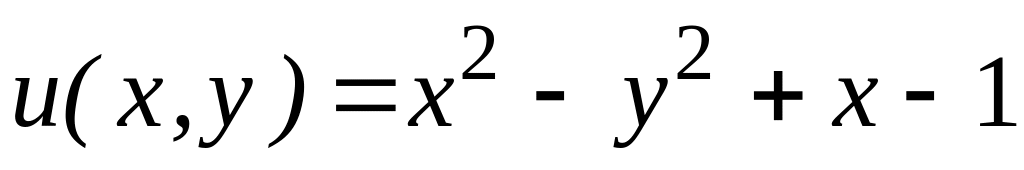 ,
, 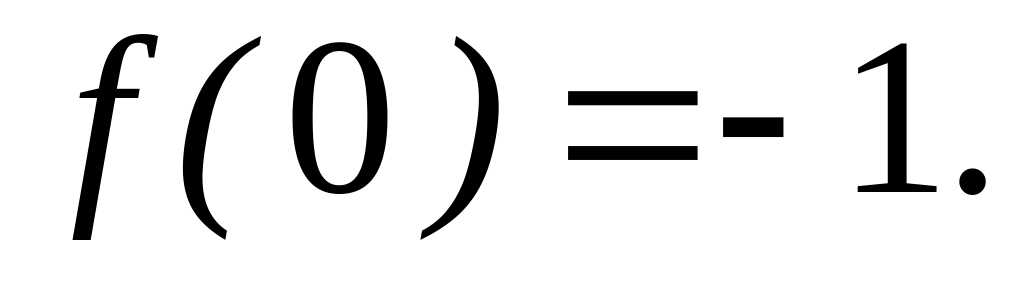
 ,
,
 ,
, 
,
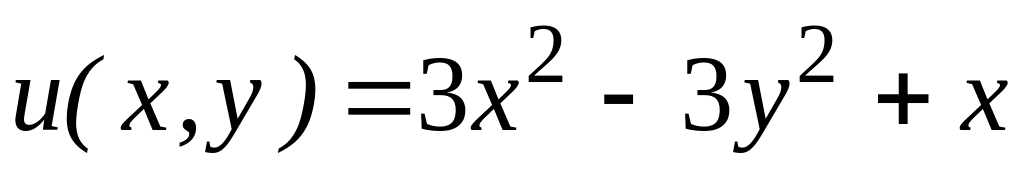 ,
,
 ,
,
 ,
, 
 ,
,
,
 ,
, 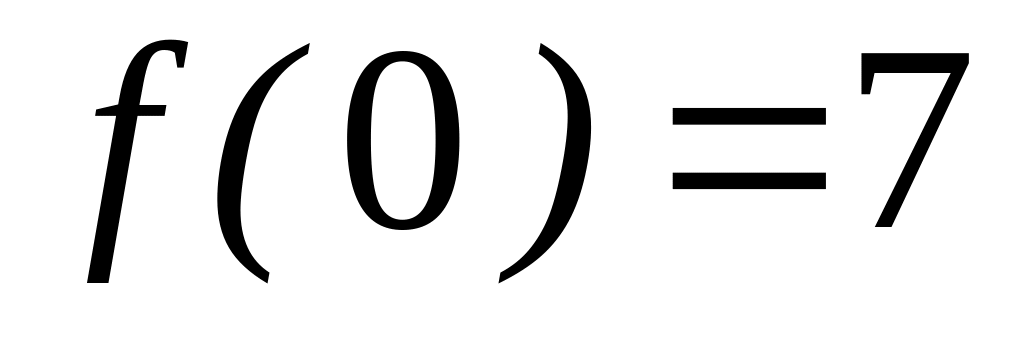

,
 ,
,
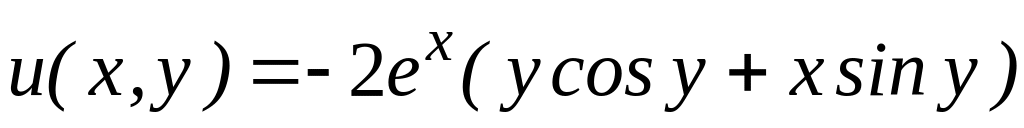 ,
,

 ,
, 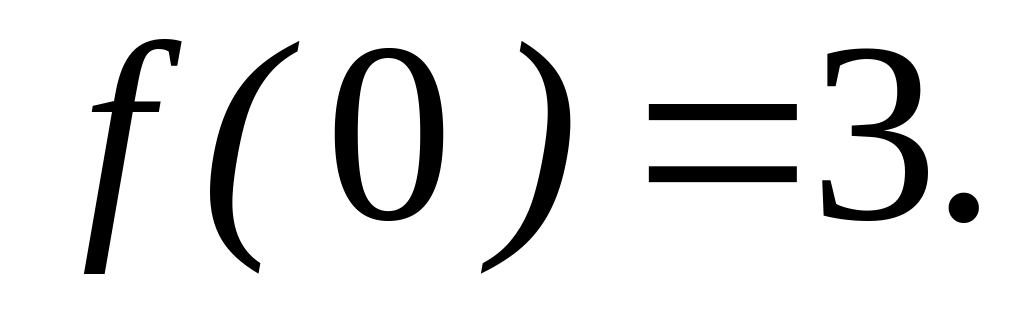
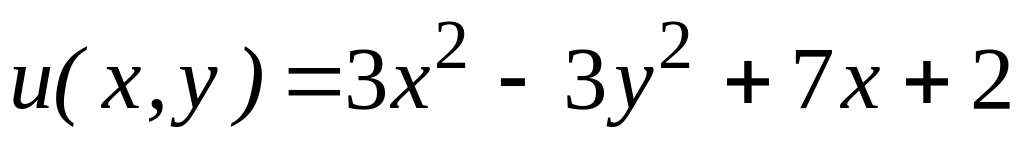 ,
,
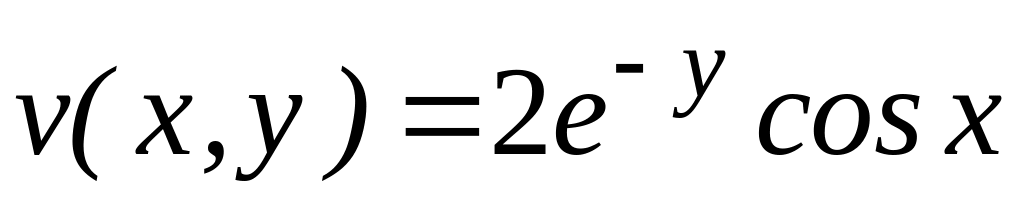 ,
, 
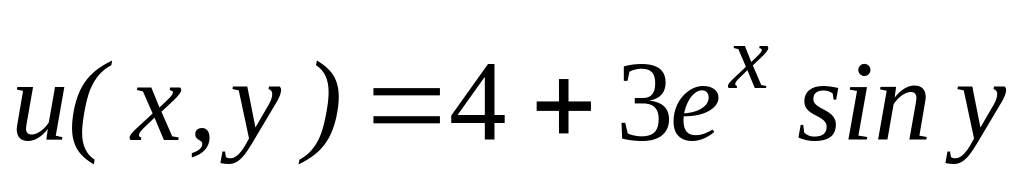 ,
, 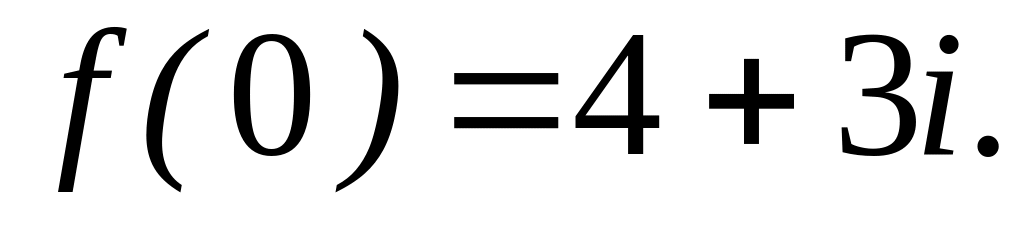

,
4.2.4 Обчислити інтеграл від функції комплексної змінної по заданій кривій.
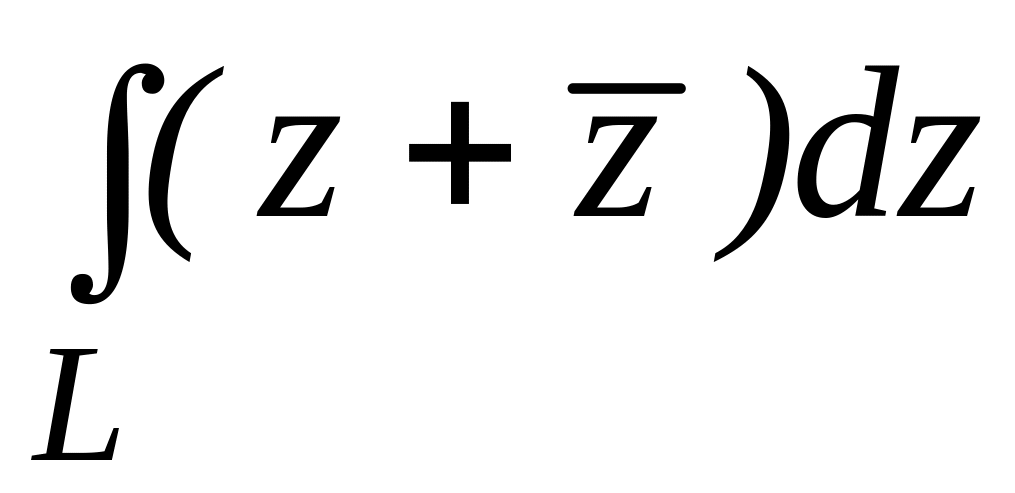 ;
; 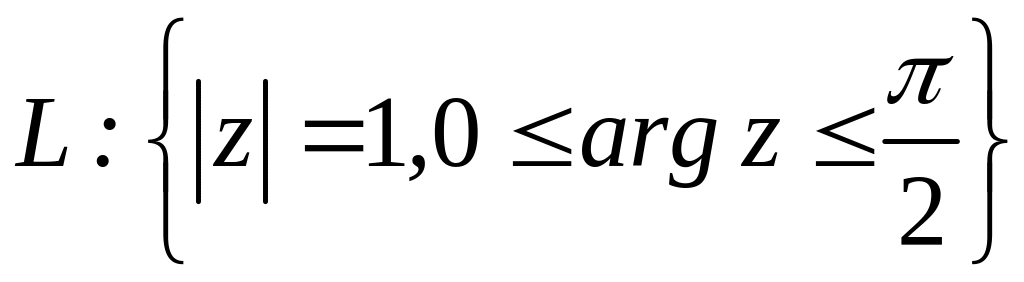 .
.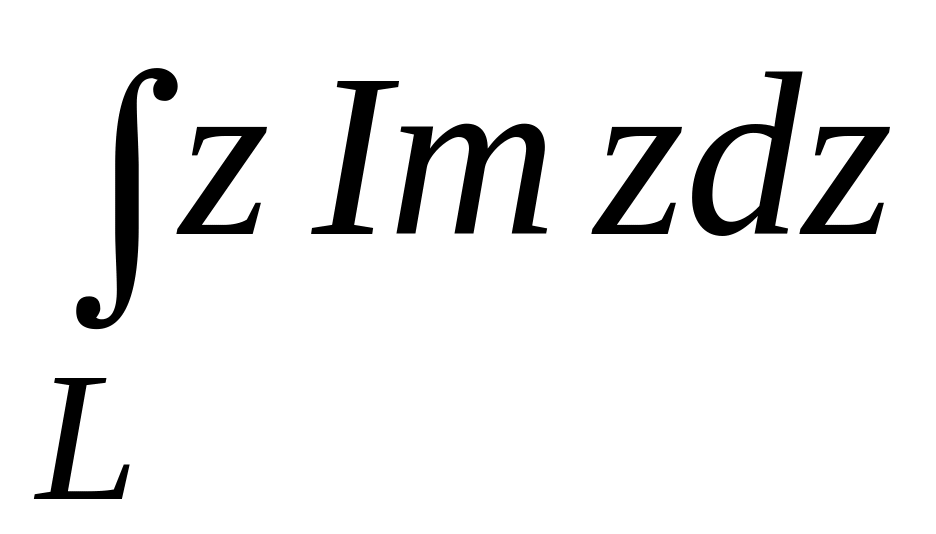 ;
; 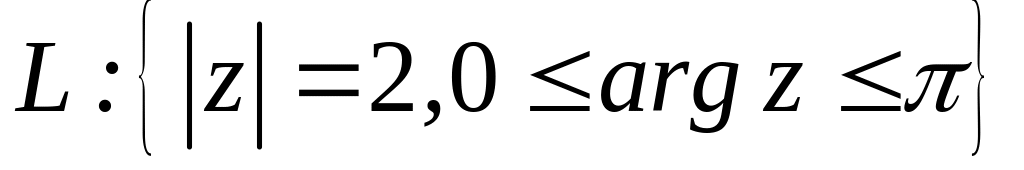 .
.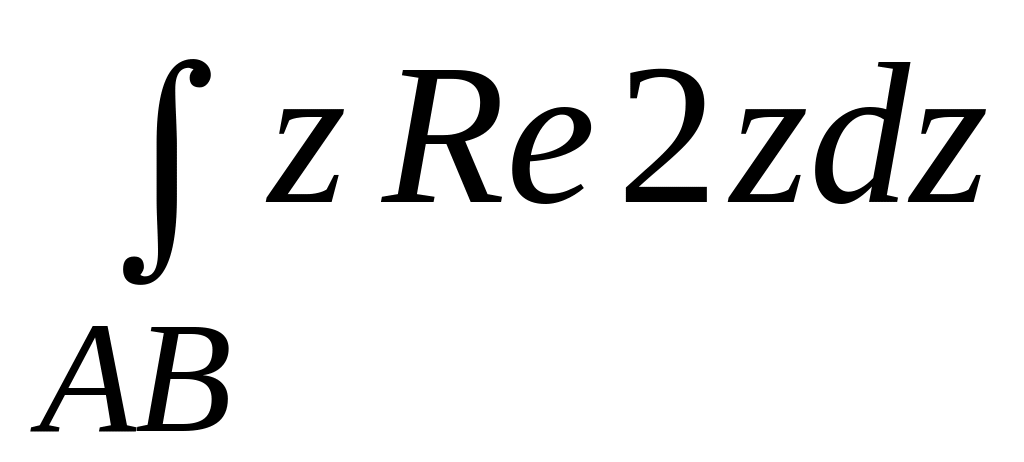 ;
;  - відрізок прямої,
- відрізок прямої,
 ,
,
 .
. ;
; 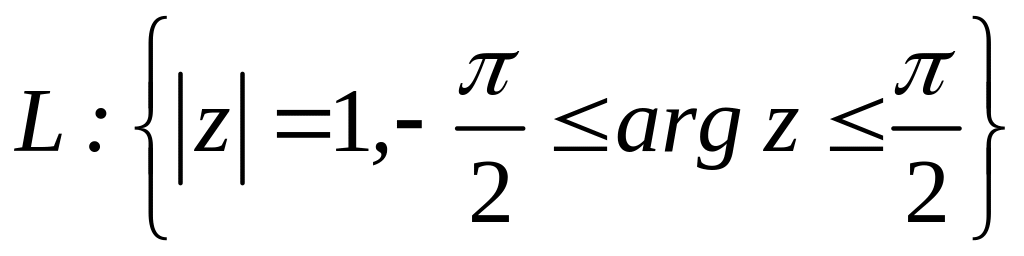 .
. ;
.
;
. ;
- відрізок прямої,
;
- відрізок прямої,
 ,
,
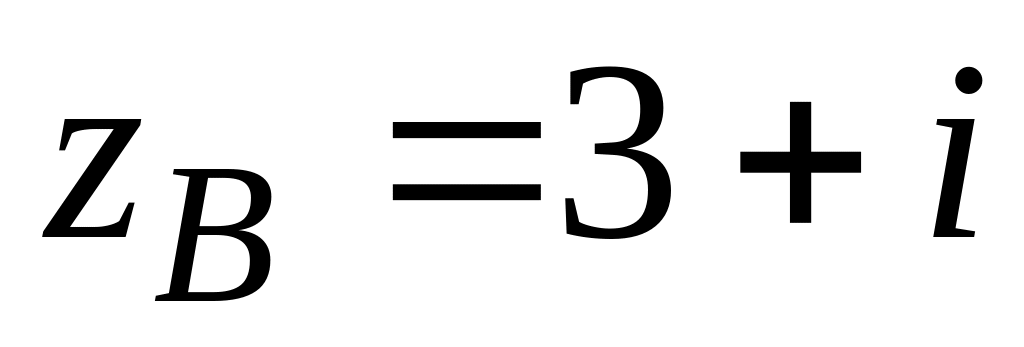 .
. ;
.
;
. ;
;  .
. ;
- відрізок прямої,
;
- відрізок прямої,
 ,
,
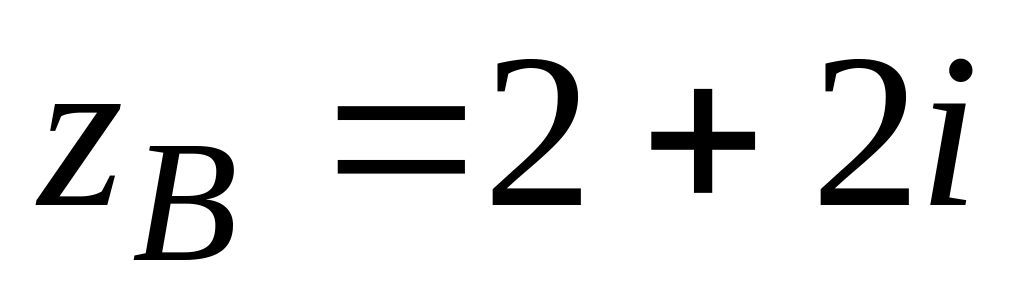 .
. ;
; 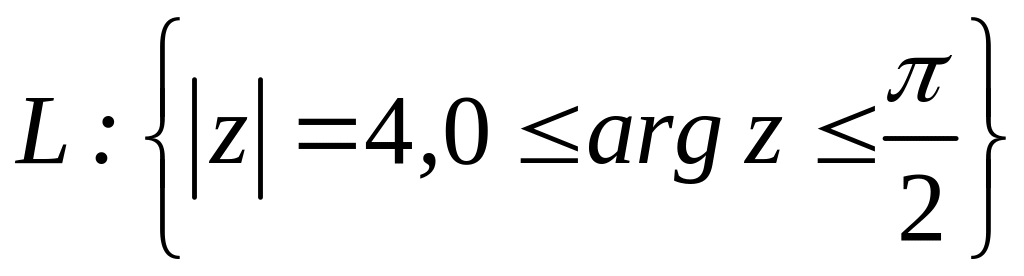 .
.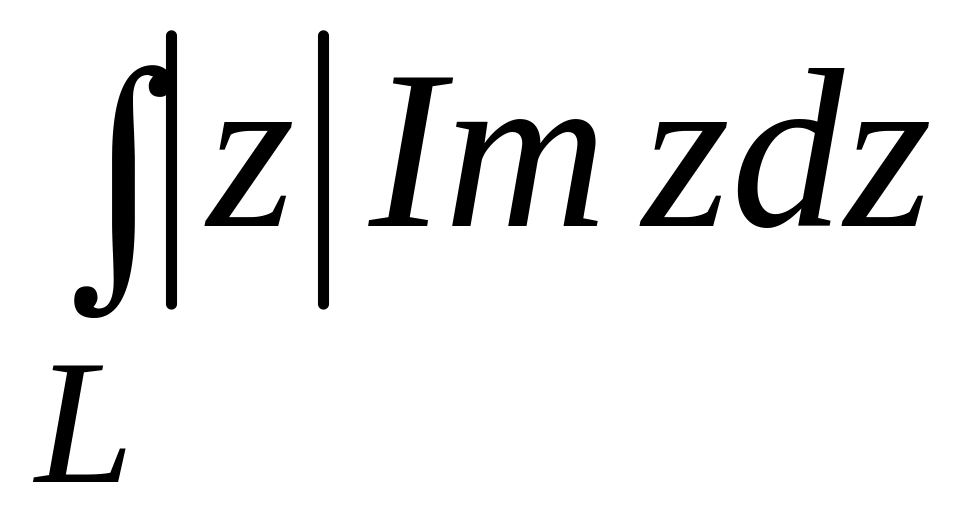 ;
.
;
. ;
- відрізок прямої,
,
;
- відрізок прямої,
,
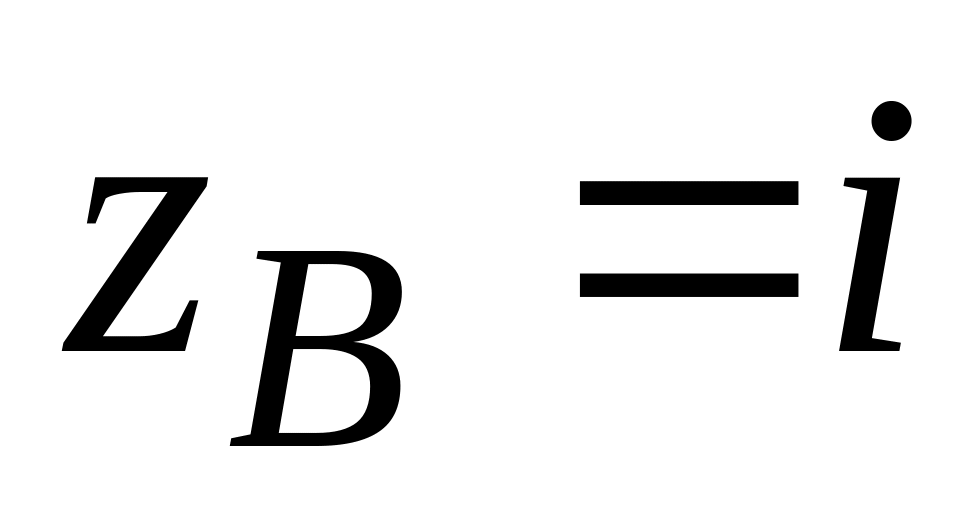 .
.; .
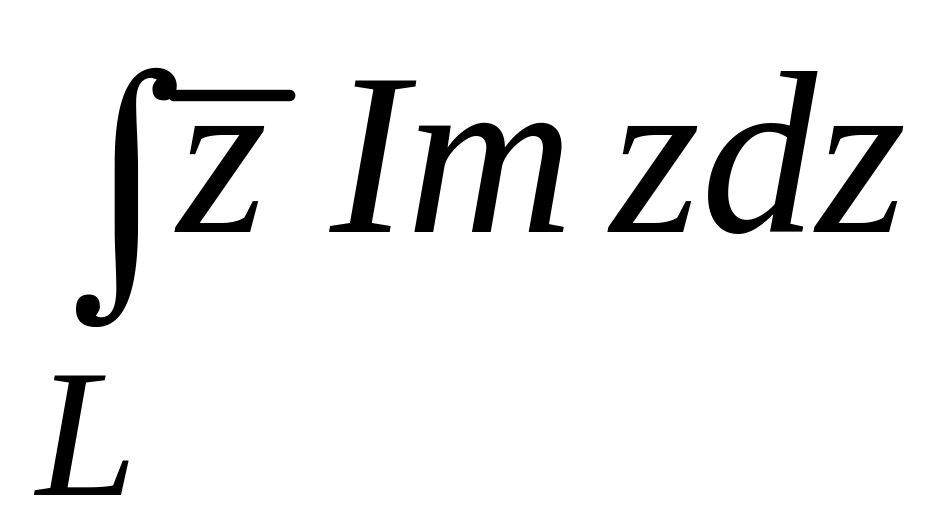 ;
;  .
. ;
- відрізок прямої,
,
;
- відрізок прямої,
,
 .
. ;
; 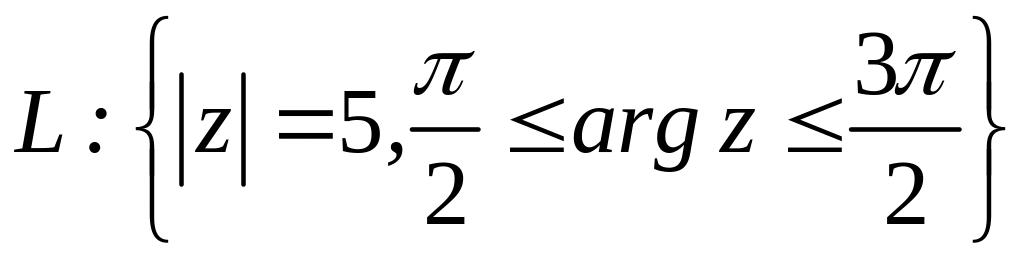 .
. ;
.
;
. ;
- відрізок прямої,
,
;
- відрізок прямої,
,
 .
. ;
;  .
.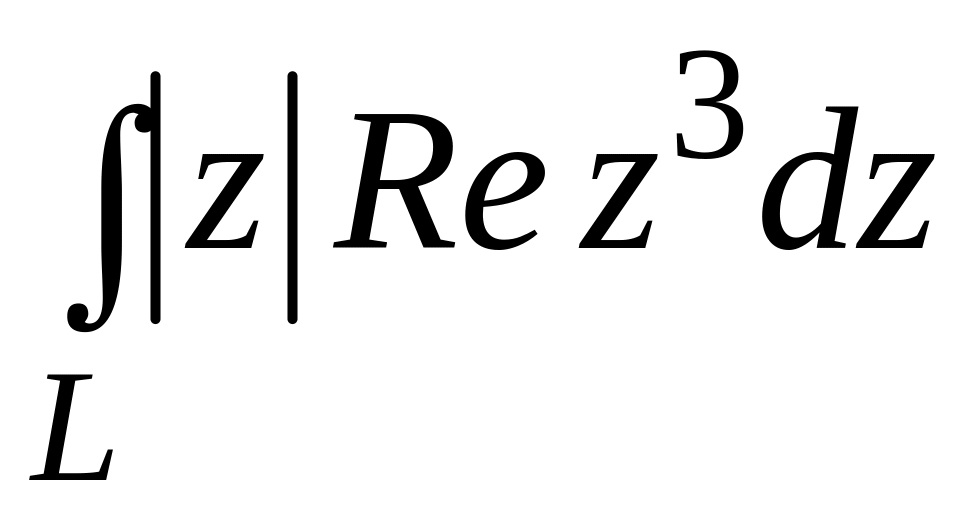 ;
;  .
.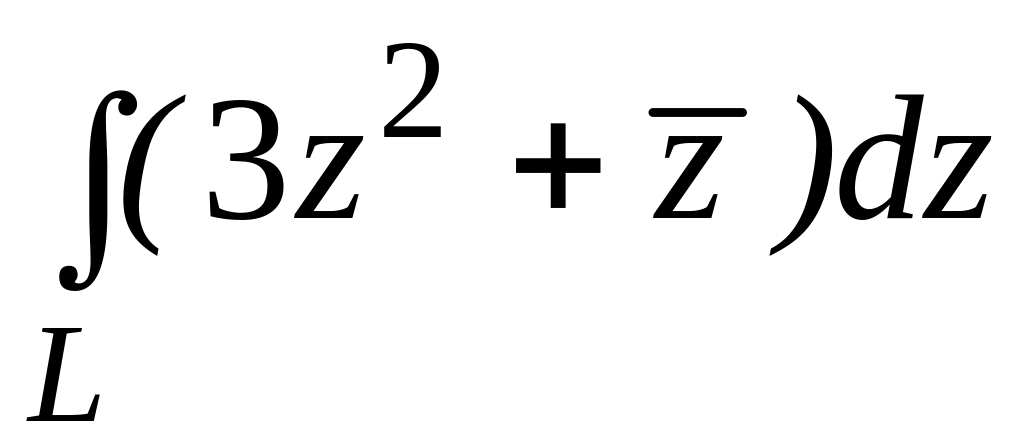 ;
; 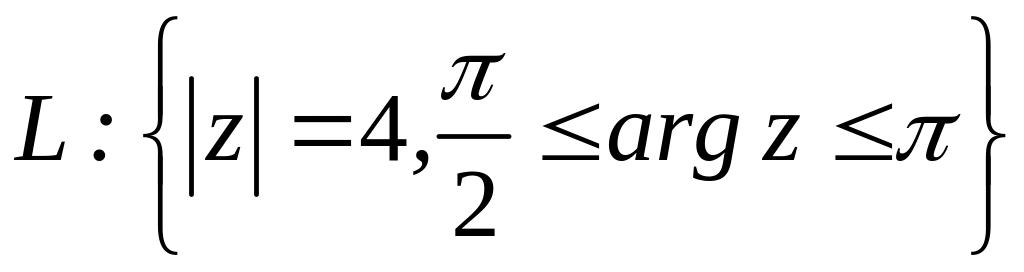 .
.; - відрізок прямої, ,
 .
.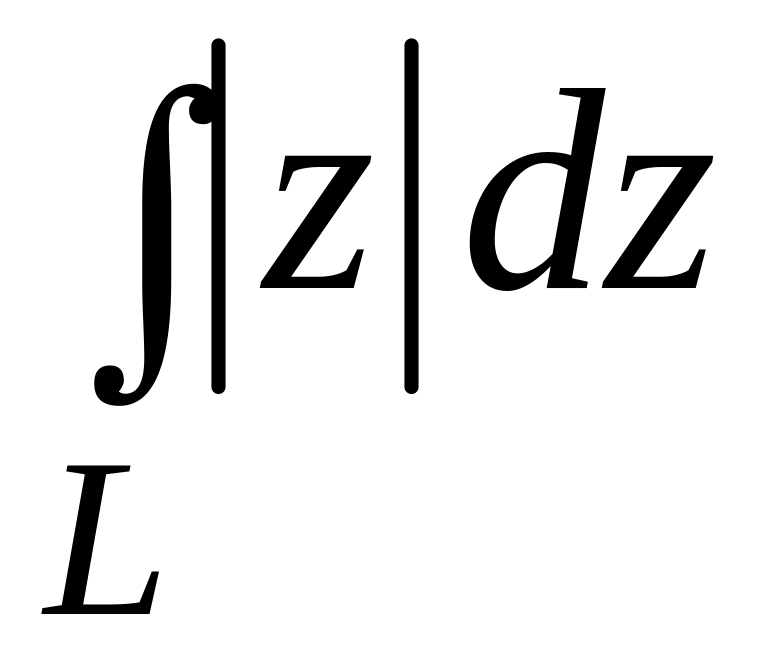 ;
;  .
.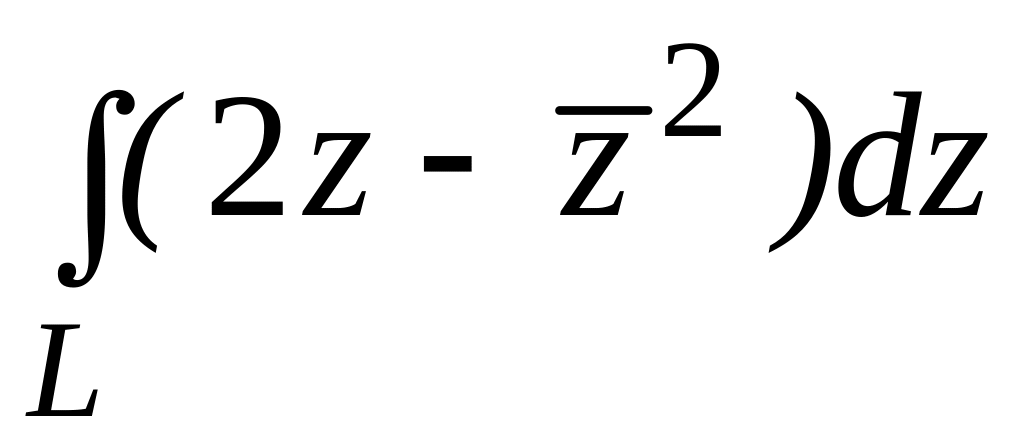 ;
.
;
.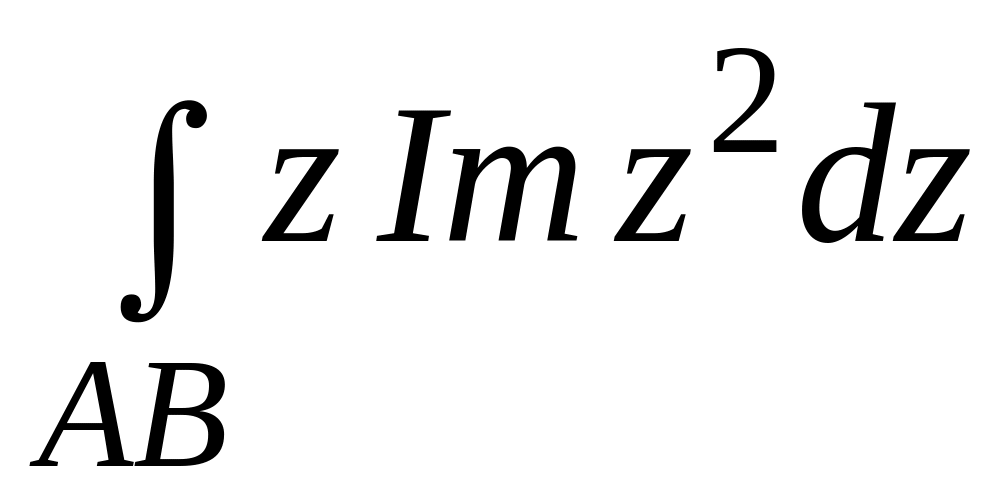 ;
- відрізок прямої,
,
;
- відрізок прямої,
,
 .
. ;
; 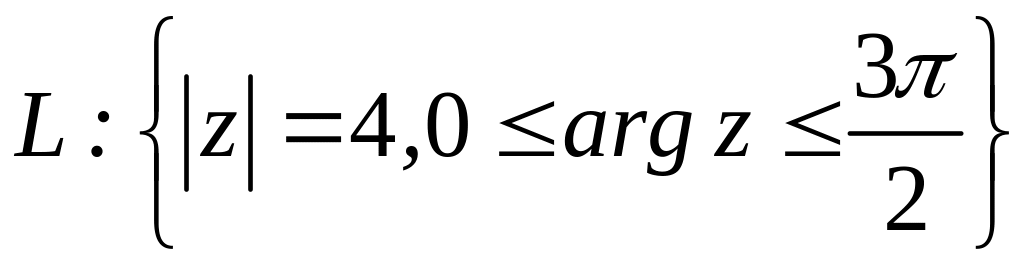 .
.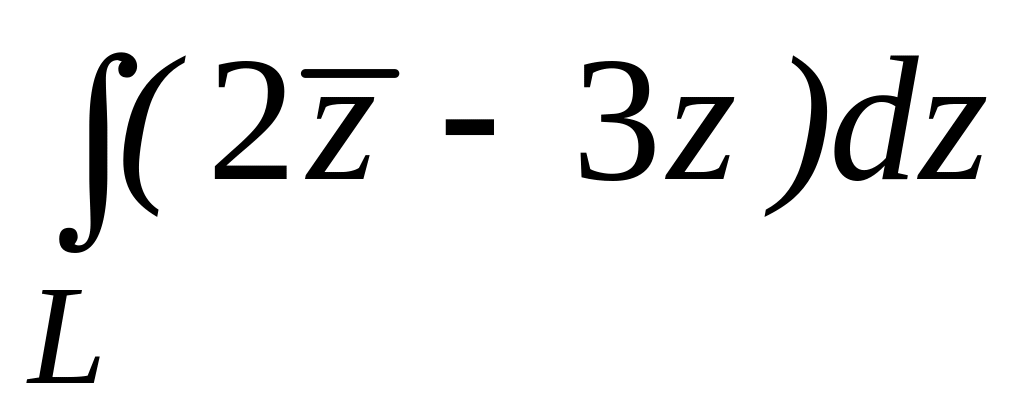 ;
.
;
.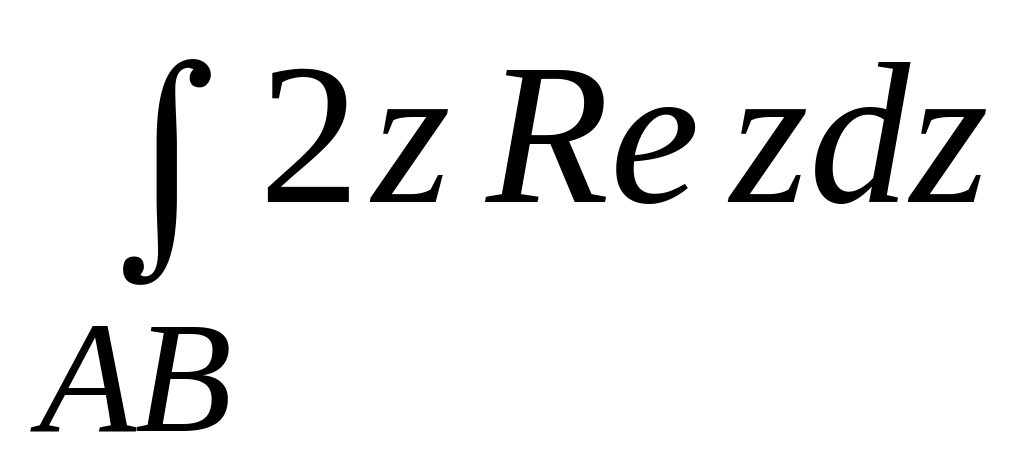 ;
- відрізок прямої,
,
.
;
- відрізок прямої,
,
. ;
; 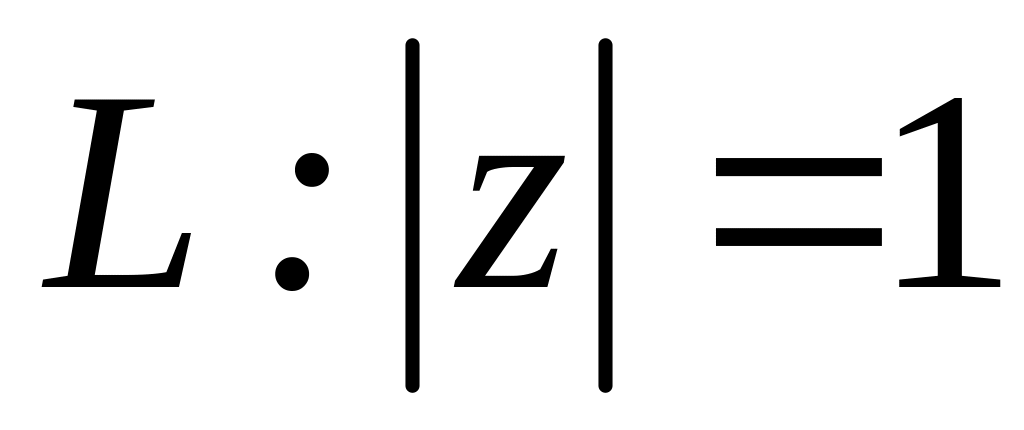 .
.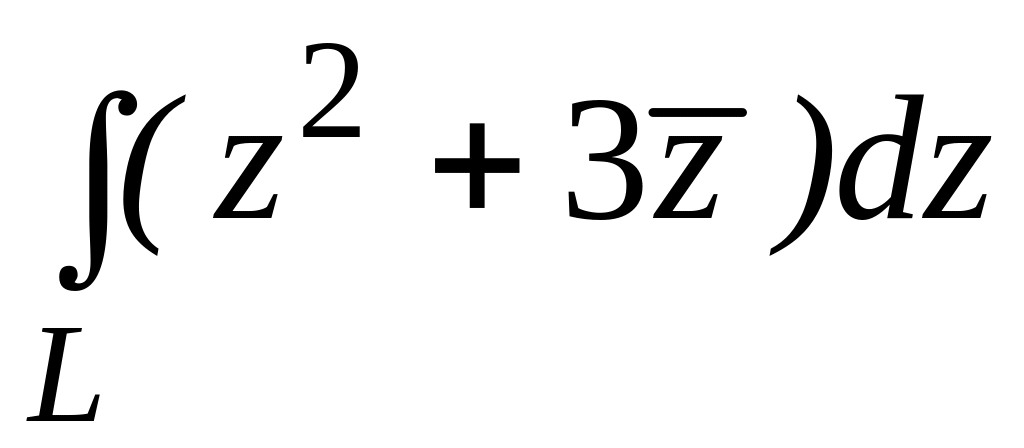 ;
; 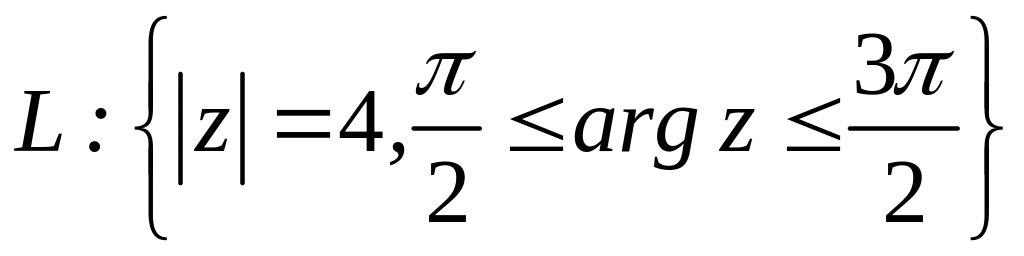 .
.; - відрізок прямої, , .
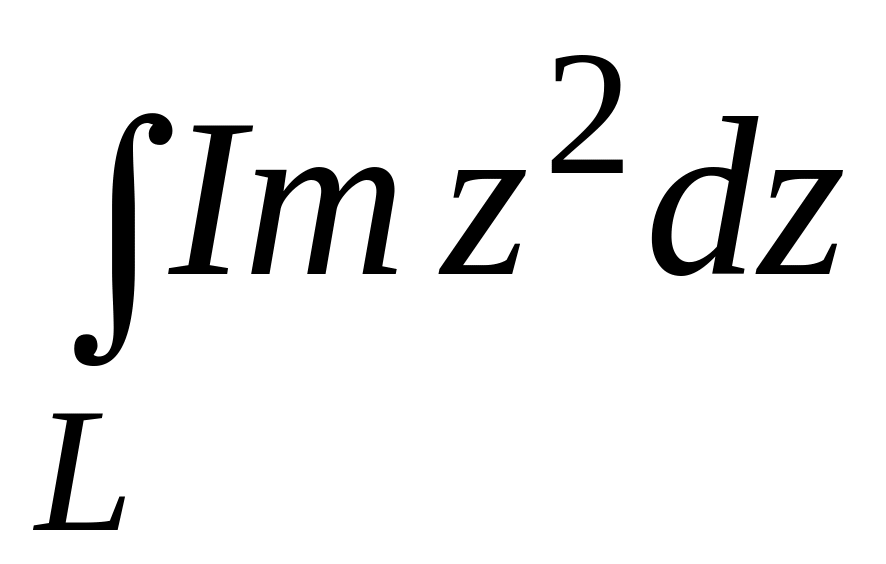 ;
;  .
.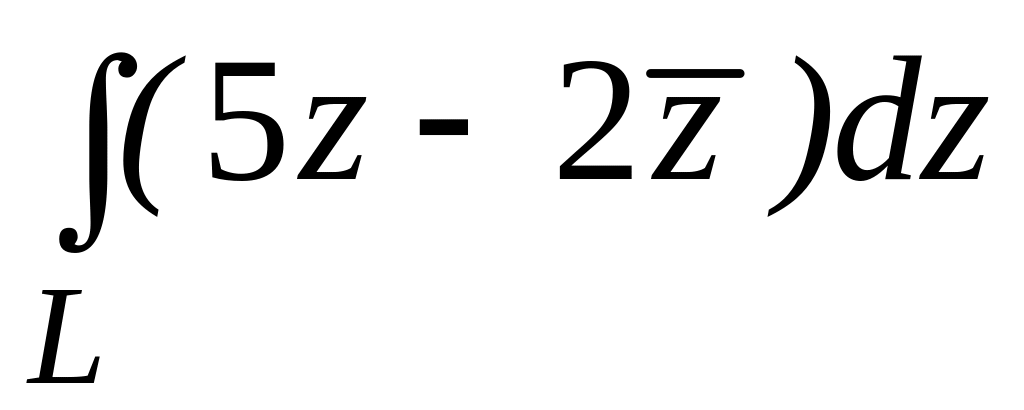 ;
.
;
. ;
;  .
.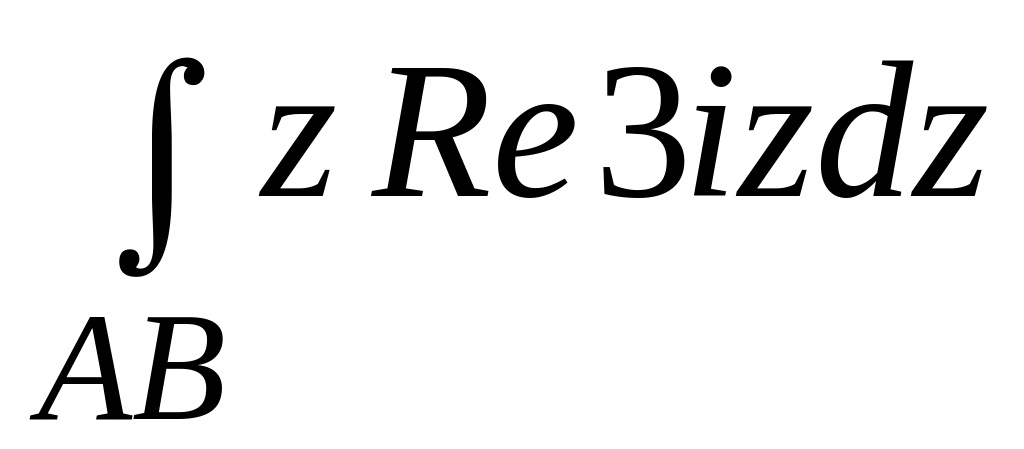 ;
- відрізок прямої,
;
- відрізок прямої,
 ,
.
,
.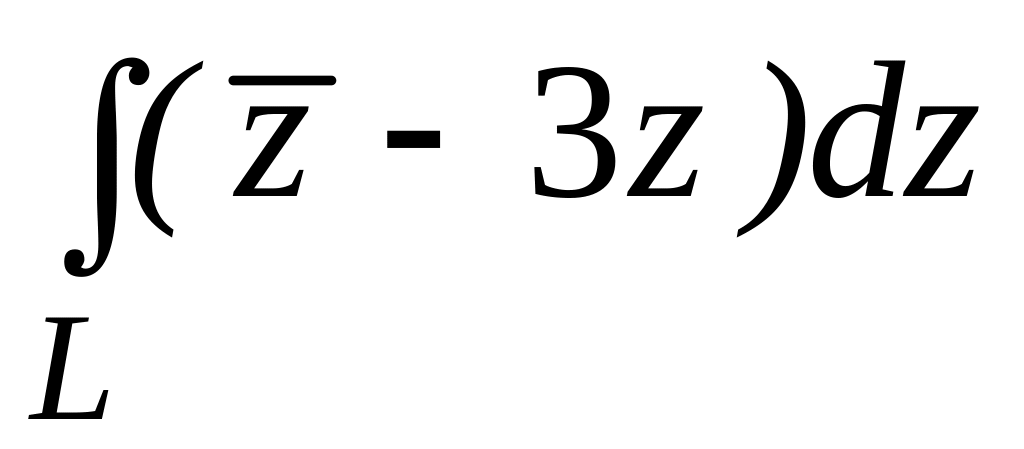 ;
.
;
. ;
.
;
.; - відрізок прямої, , .
 ;
.
;
. ;
.
;
.; - відрізок прямої, ,
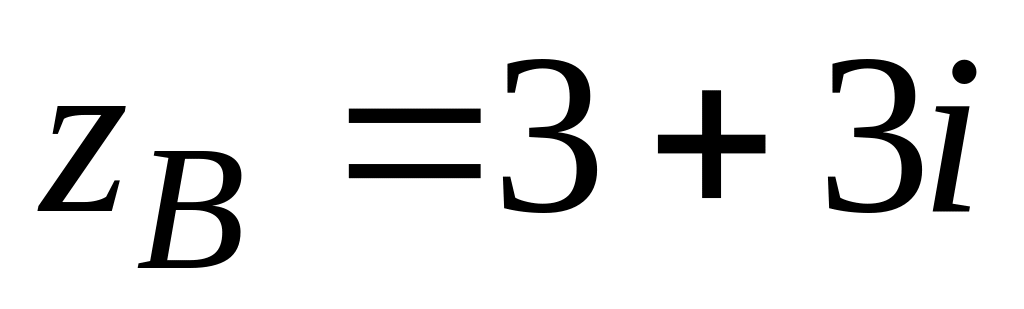 .
. ;
; 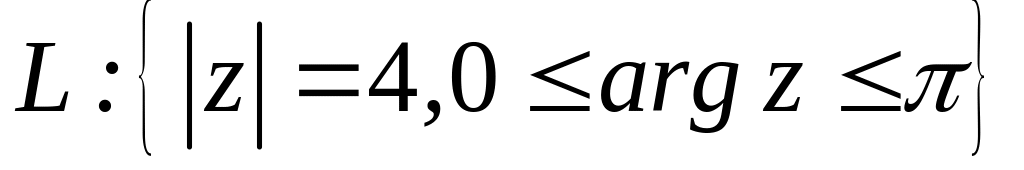 .
. ;
.
;
. ;
- відрізок прямої,
;
- відрізок прямої,
 ,
,
 .
. ;
.
;
.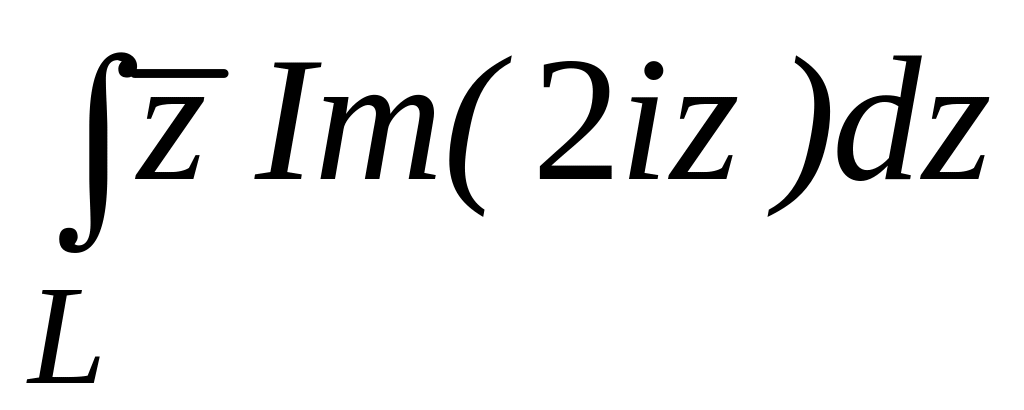 ;
.
;
. ;
- відрізок прямої,
,
;
- відрізок прямої,
,
 .
.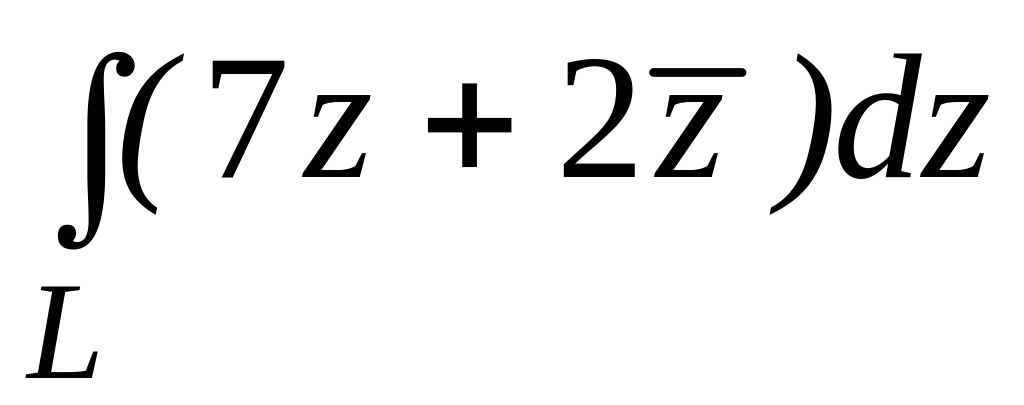 ;
;  .
.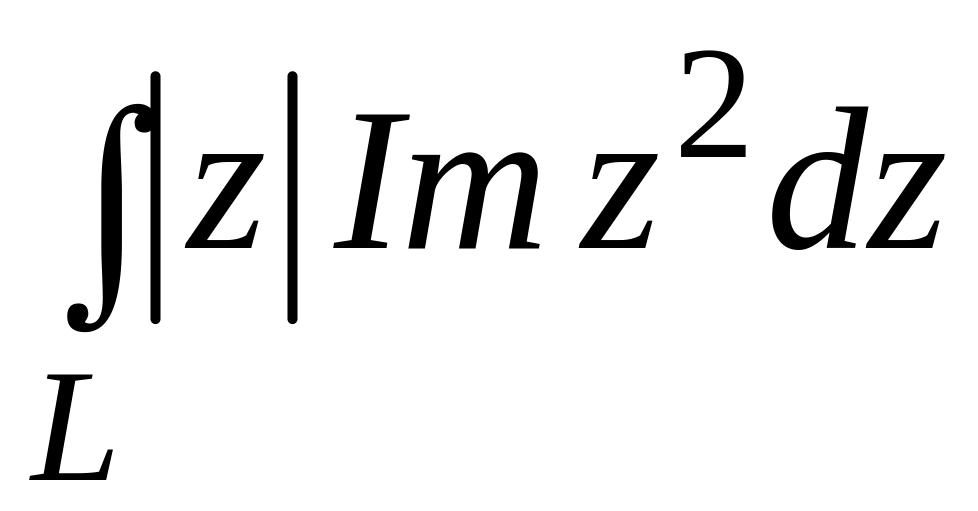 ;
.
;
.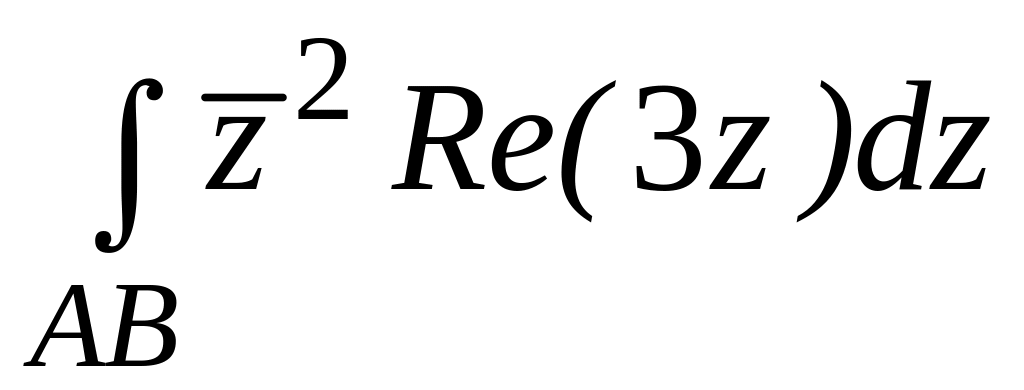 ;
- відрізок прямої,
,
;
- відрізок прямої,
,
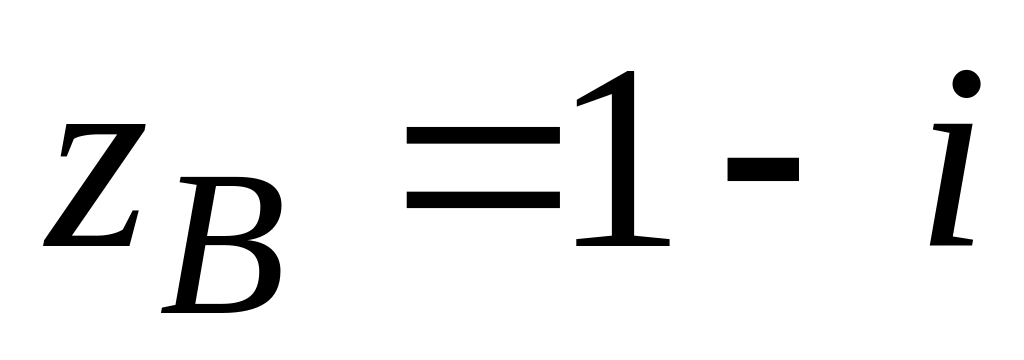 .
.
4.2.5 Обчислити інтеграл від функції комплексної змінної по відрізку прямої :
а) виразивши його через криволінійний інтеграл;
б) за формулою Ньютона-Лейбніца.
4.2.6 Обчислити інтеграли за допомогою інтегральної формули Коші та за допомогою теореми про лишки.
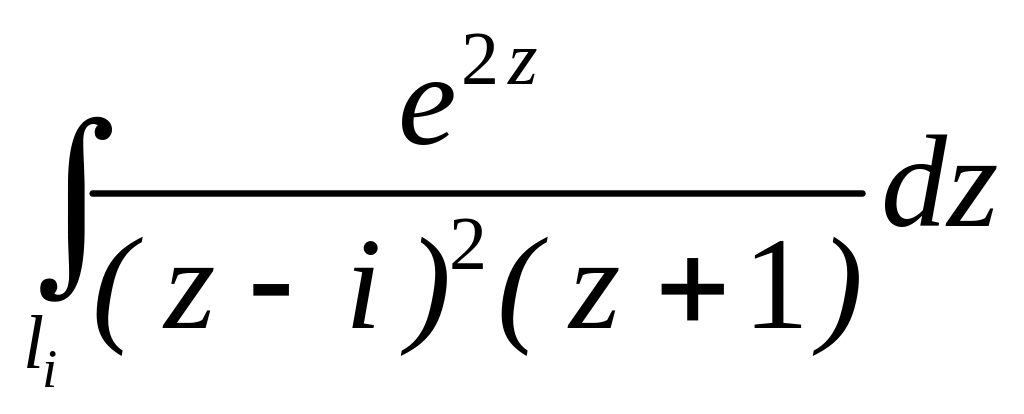
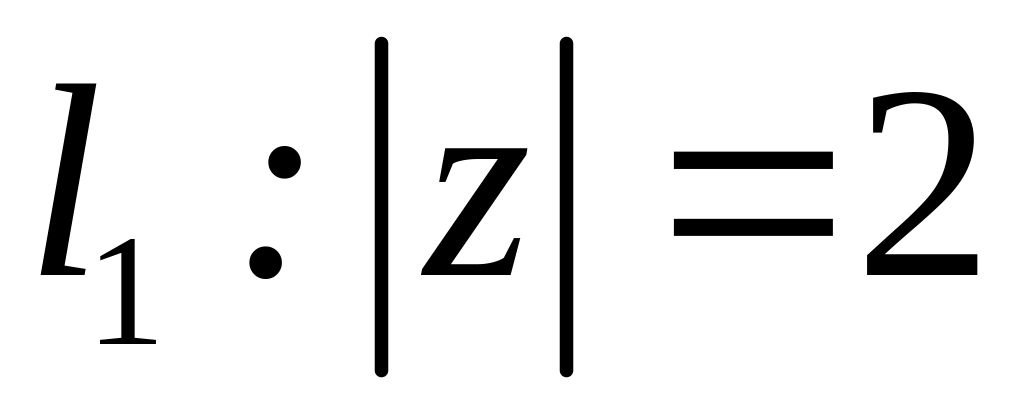 ;
;  ;
;  ;
;  .
.
 ;
; 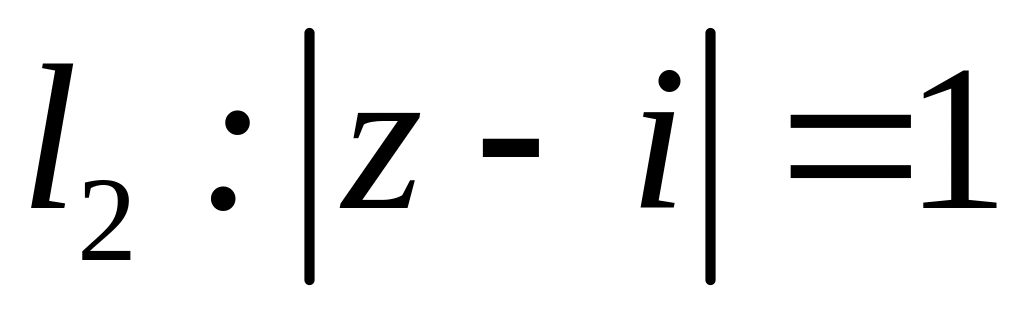 ;
;  ;
.
;
.
 ;
;  ;
; 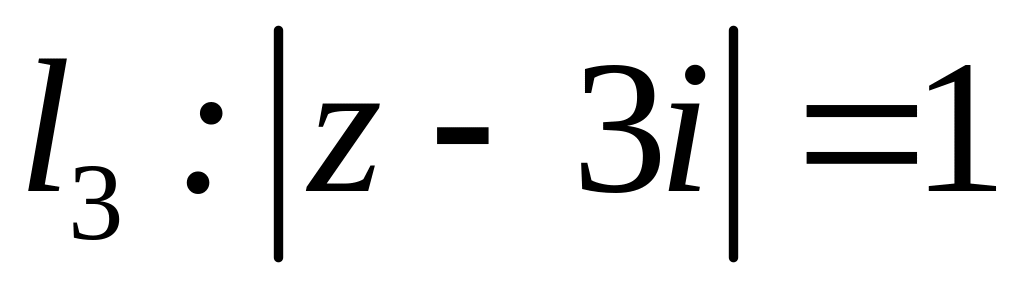 ;
; 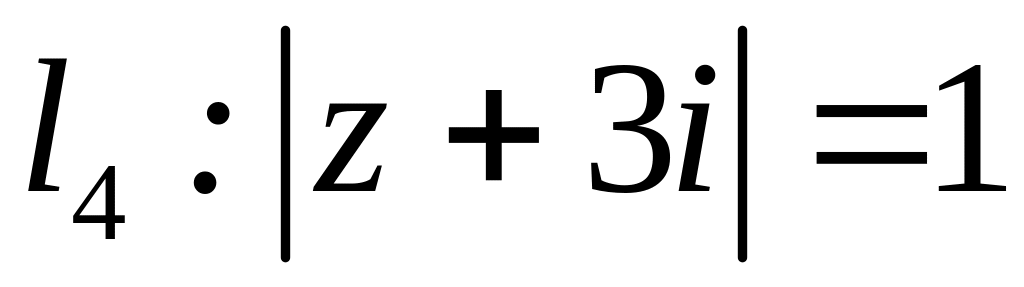 .
.
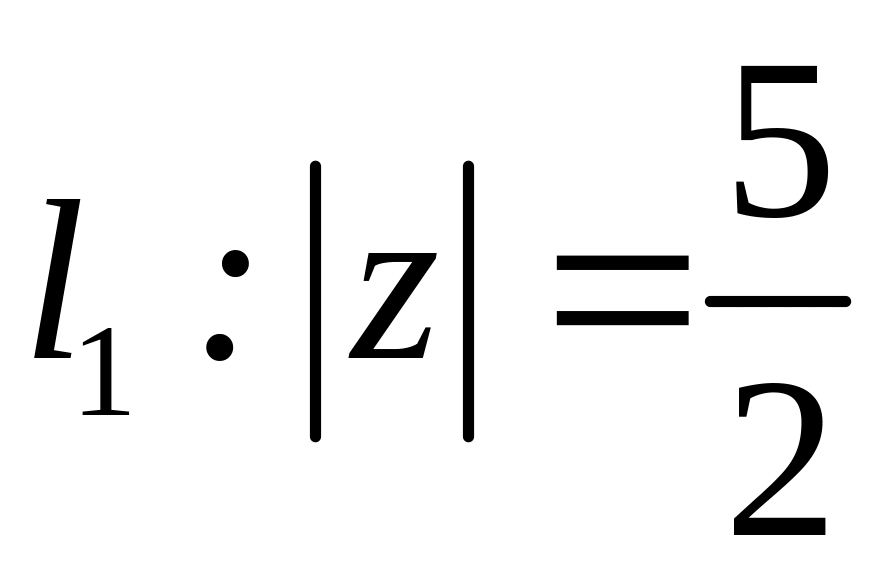 ;
;  ;
;  ;
;  .
. ;
; 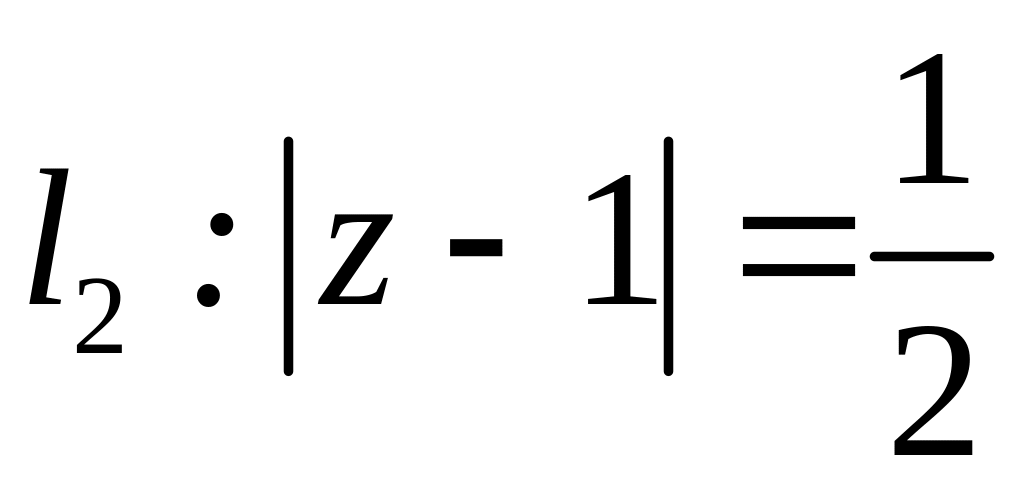 ;
;
;
;  .
.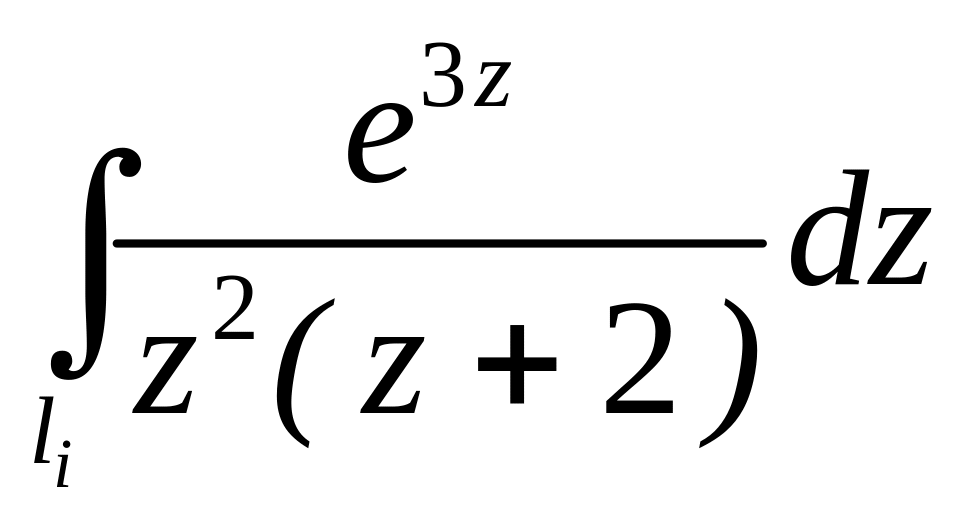 ;
;  ;
; 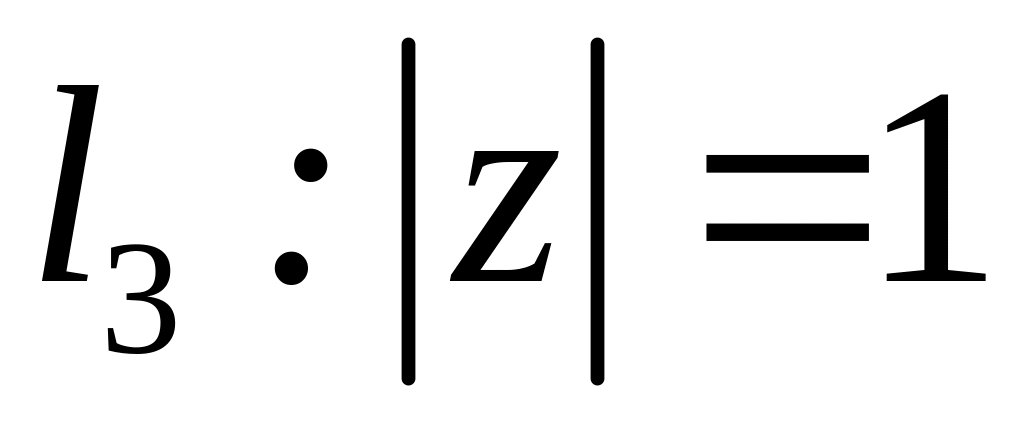 ;
.
;
.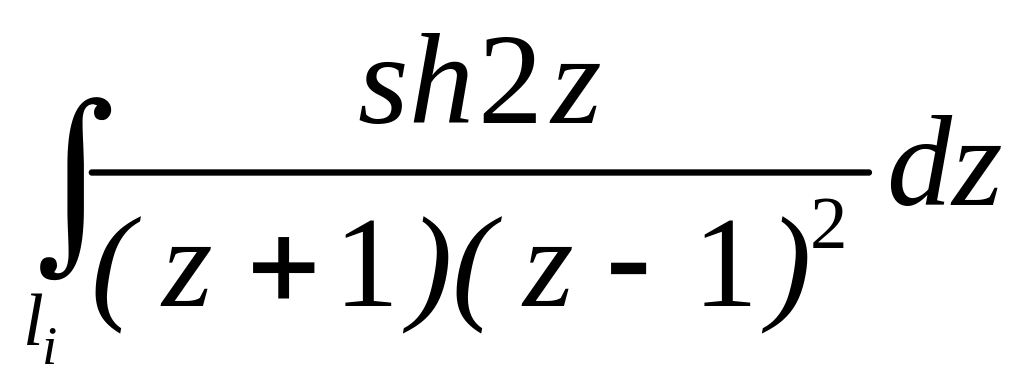 ;
;  ;
;  ;
; 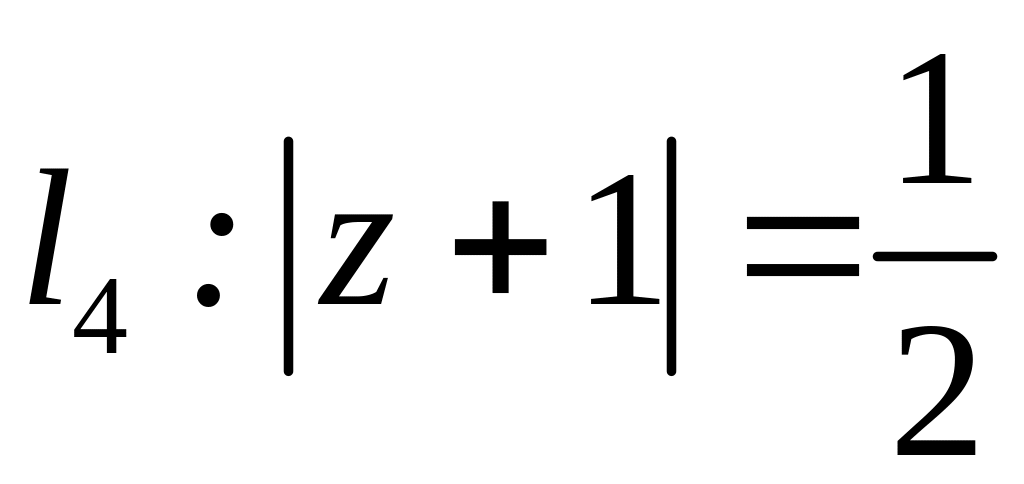 .
.
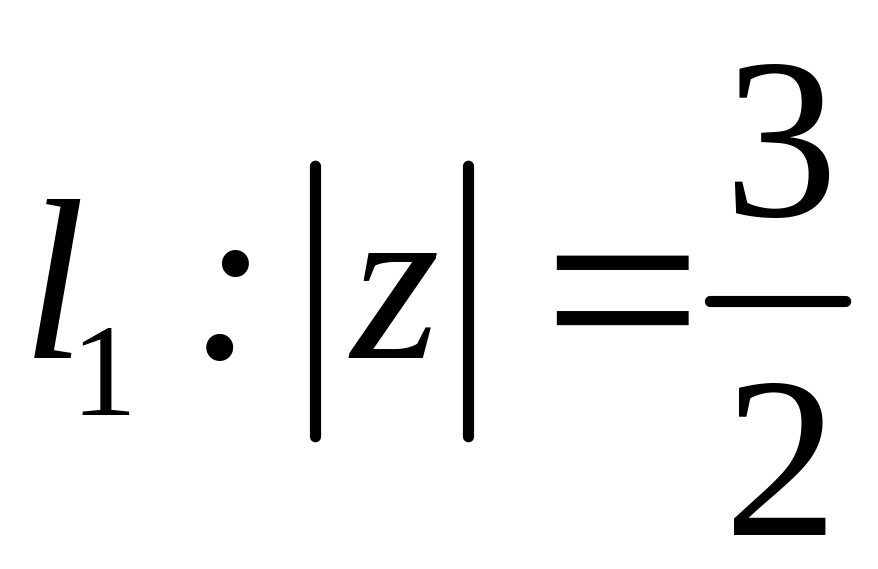 ;
;
;
;  ;
;  .
.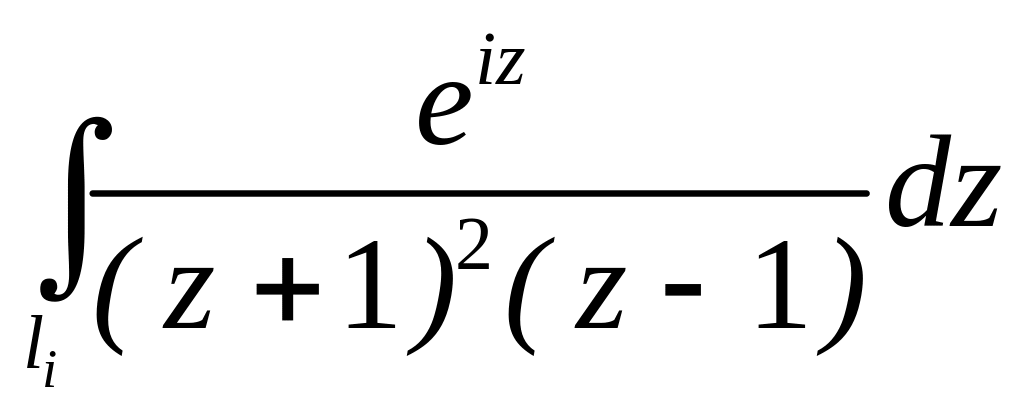 ;
; 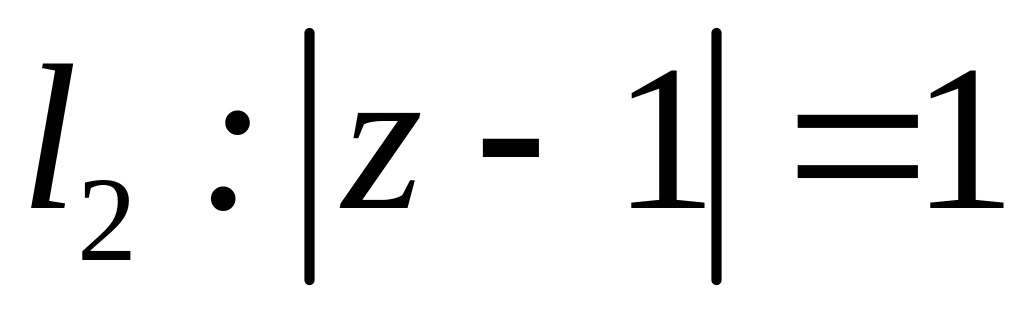 ;
;  ;
;  .
. ;
;  ;
;  ;
; 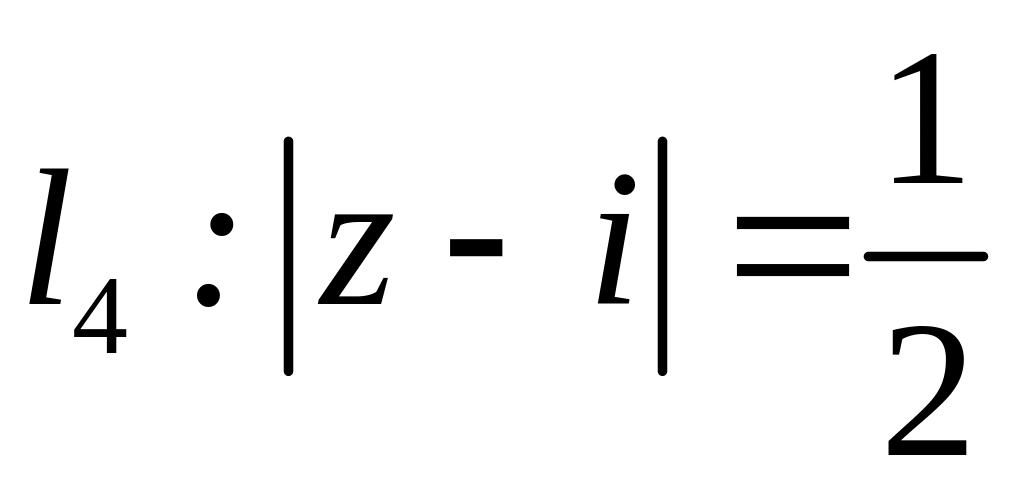 .
.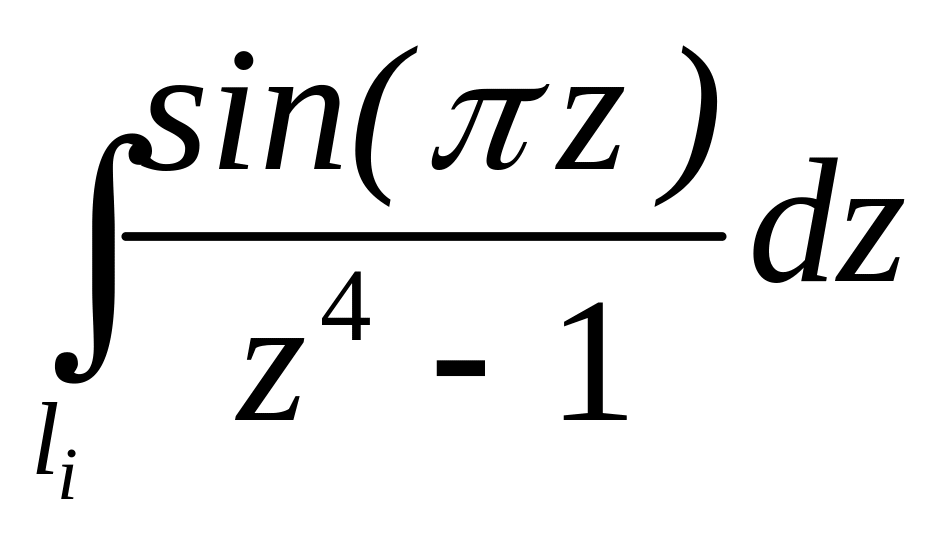 ;
;
;
.
;
;
;
. ;
;  ;
;  ;
;  .
.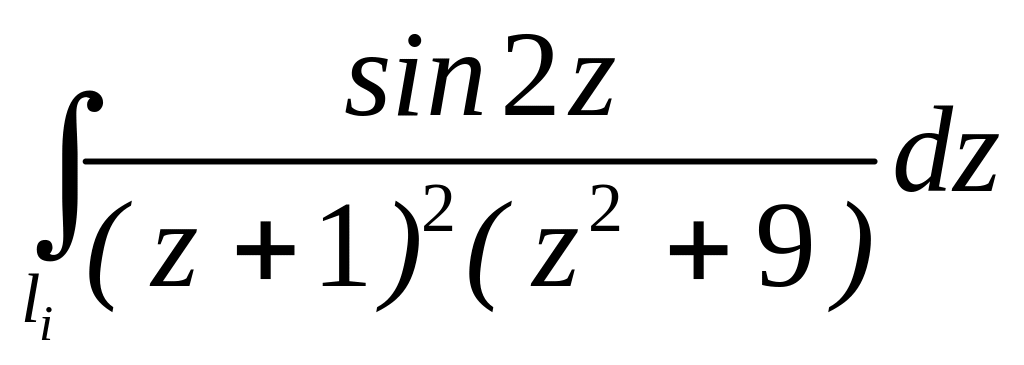 ;
;
;
.
;
;
;
. ;
;
;
.
;
;
;
. ;
; 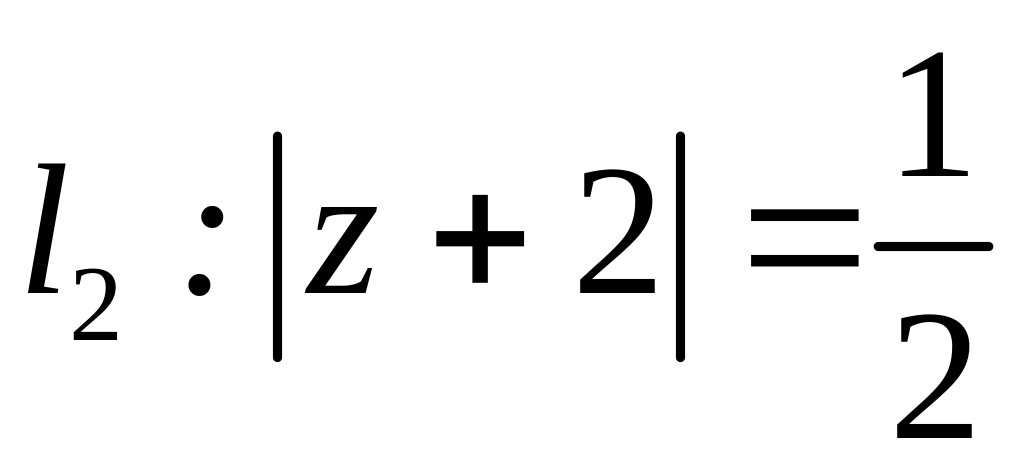 ;
; 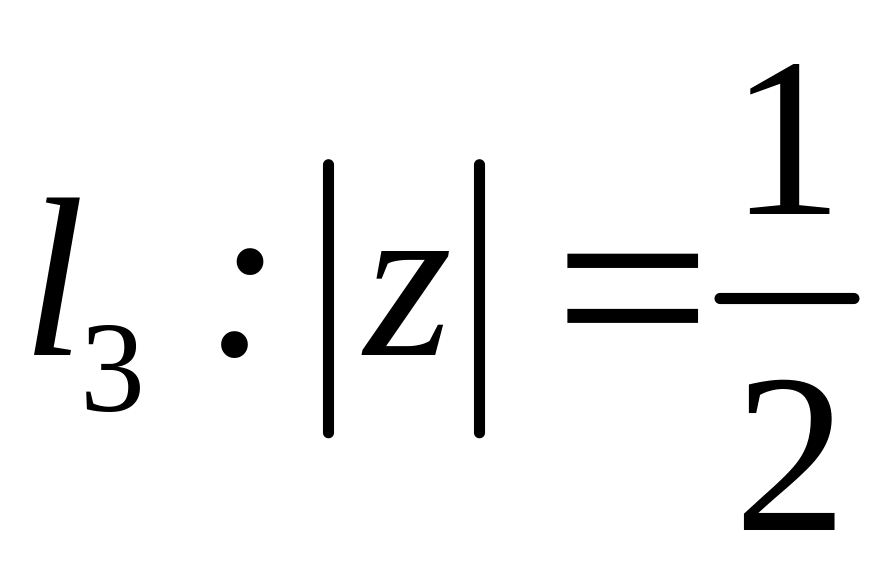 ;
.
;
.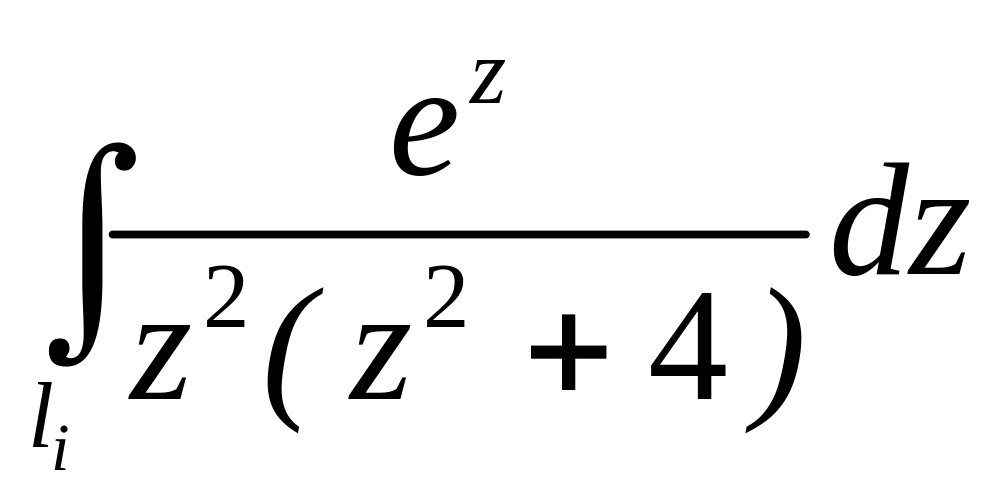 ;
;  ;
;
.
;
;
.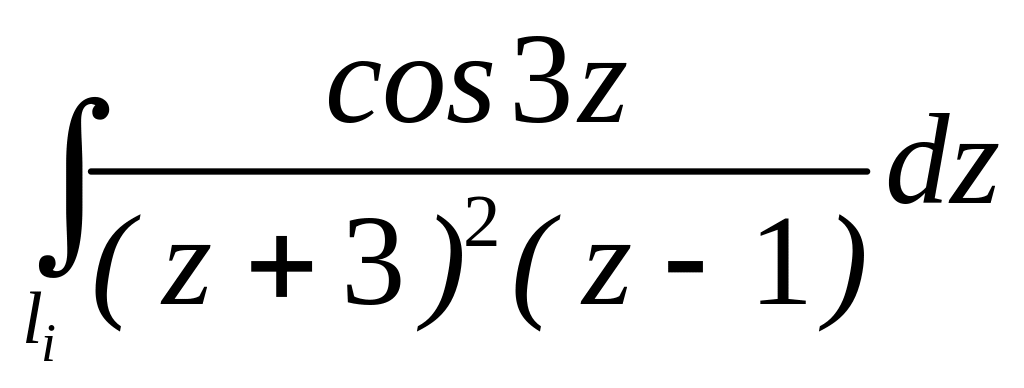 ;
;
;
; 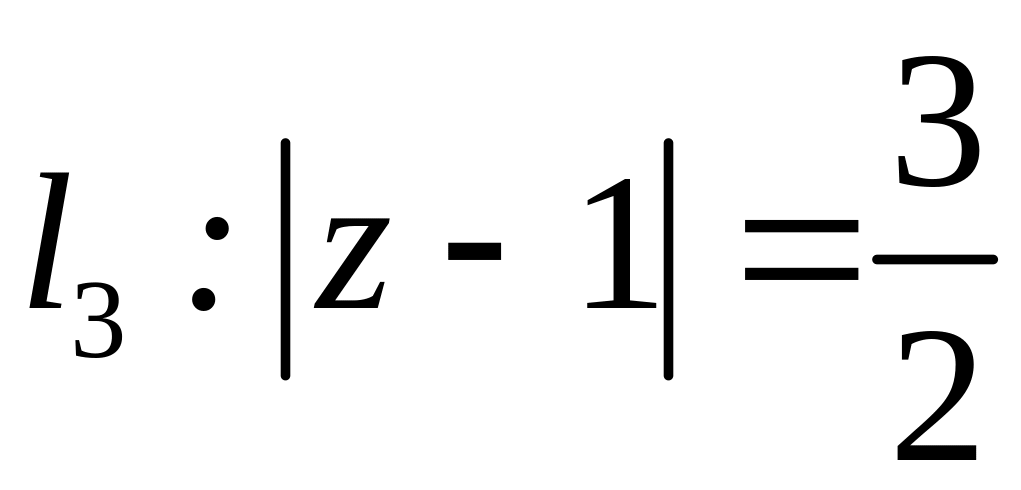 ;
; 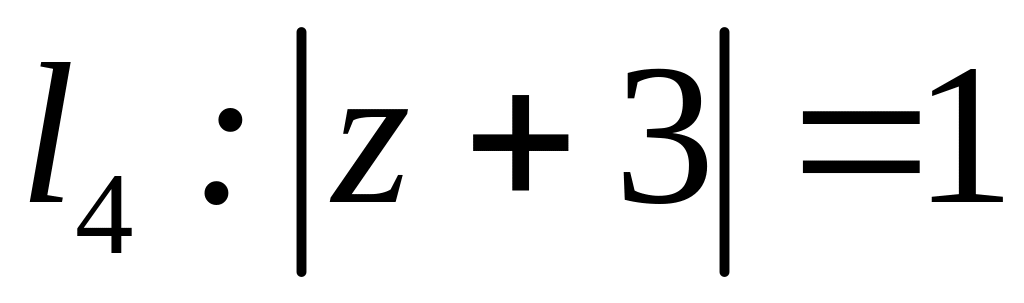 .
.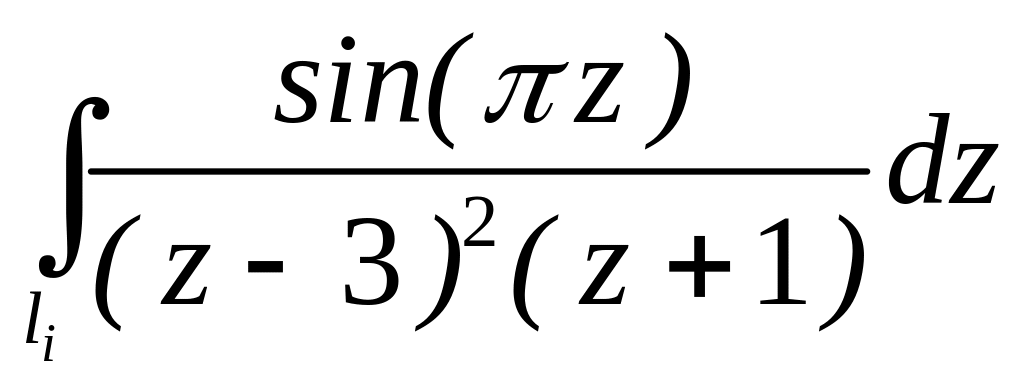
 ;
; 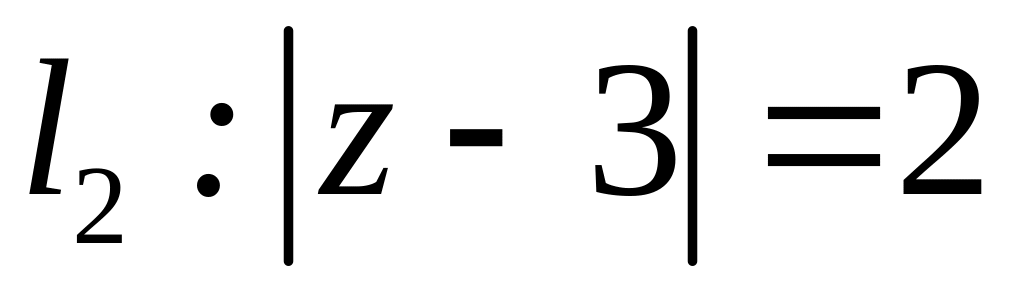 ;
;
;
;  .
.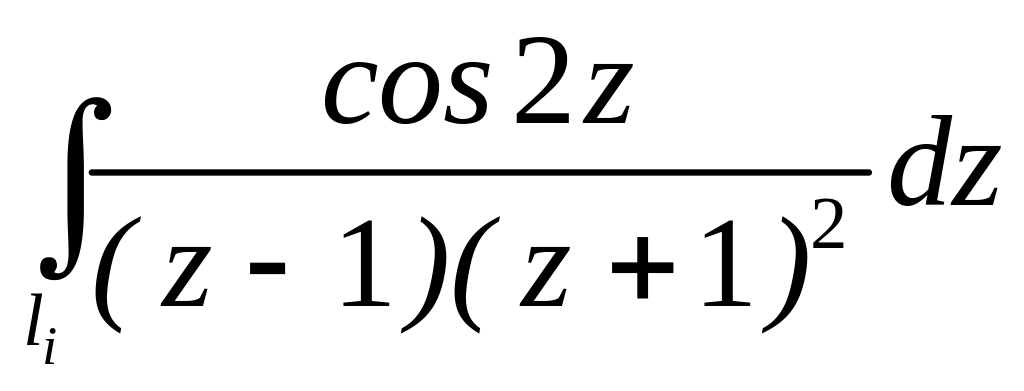 ;
;
;
;
;
; 
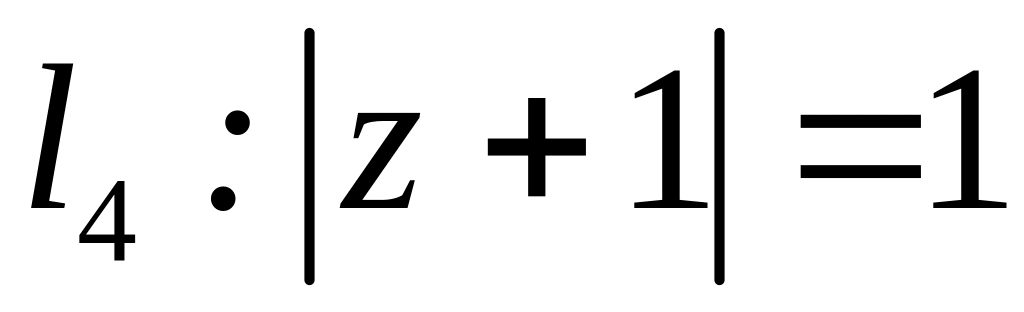 .
.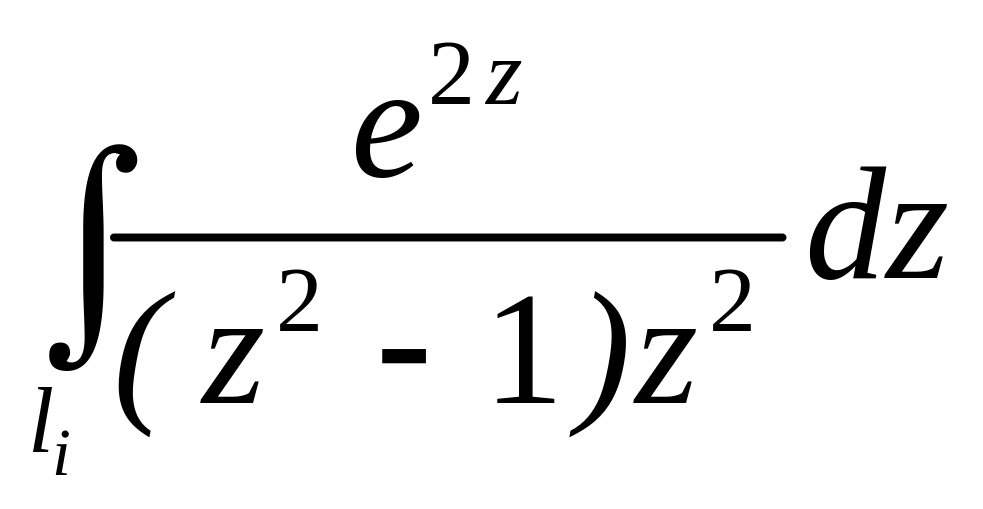 ;
;  ;
;
.
;
;
.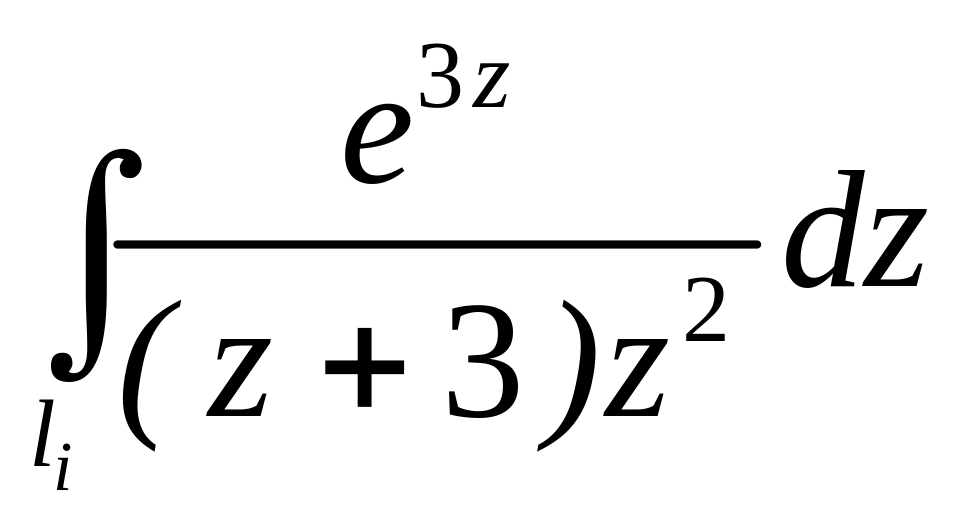 ;
;
;
;
;
; 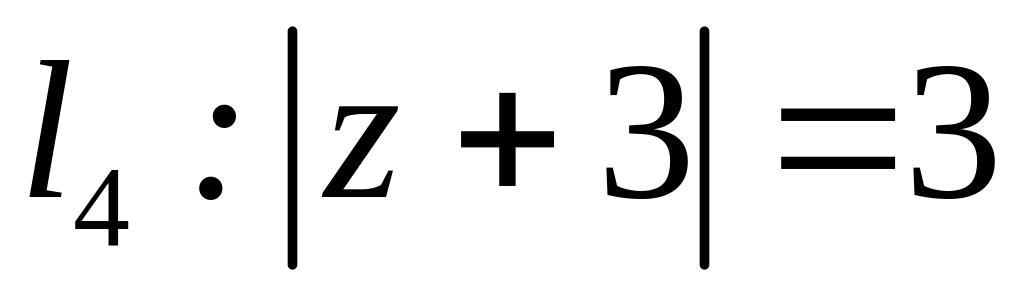 .
. ;
;
;
;  ;
.
;
. ;
;
;
; 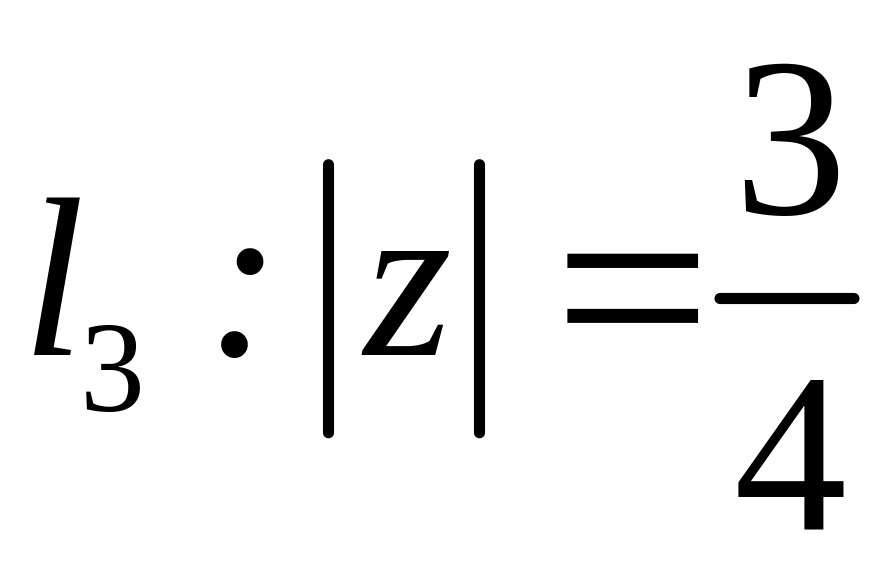 ;
;  .
.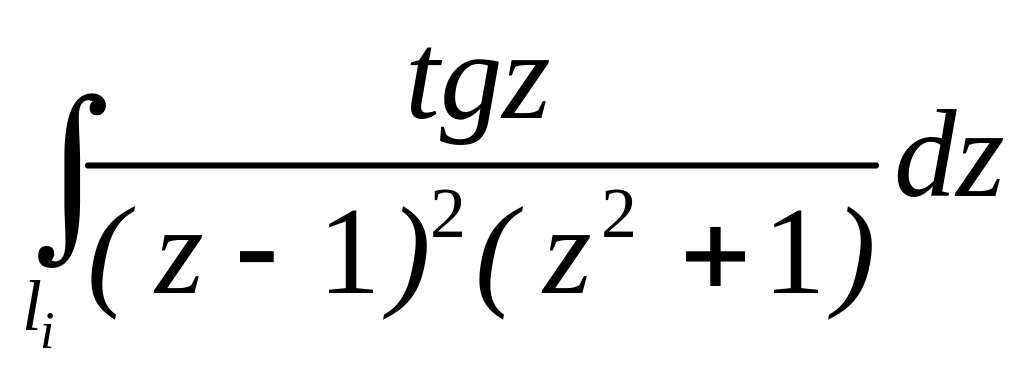 ;
; 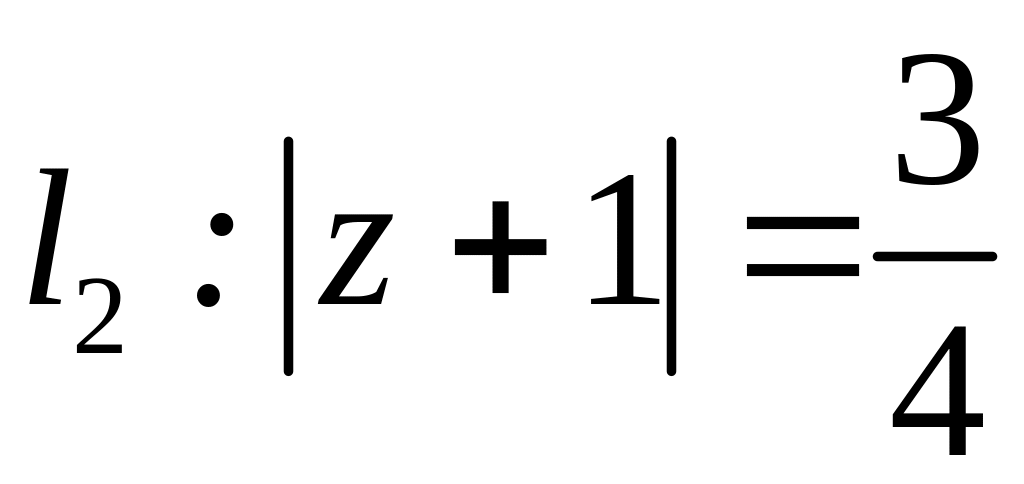 ;
;
.
;
;
. ;
;
;
;
;
; 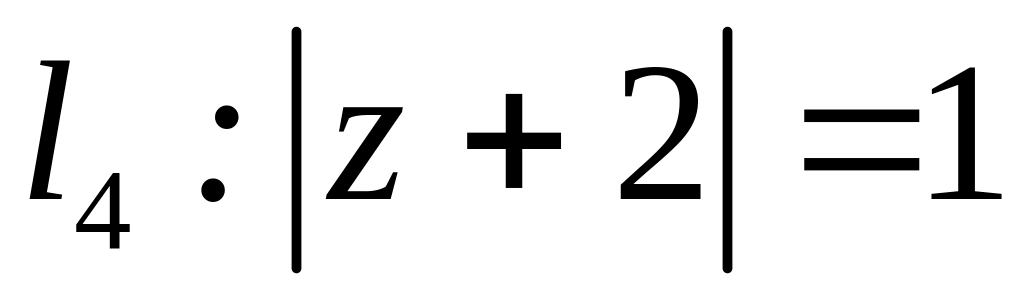 .
.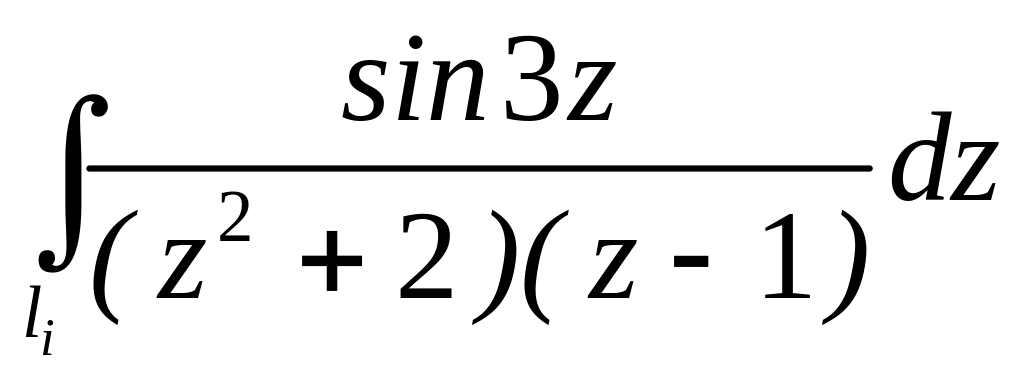 ;
;
;
;  ;
.
;
.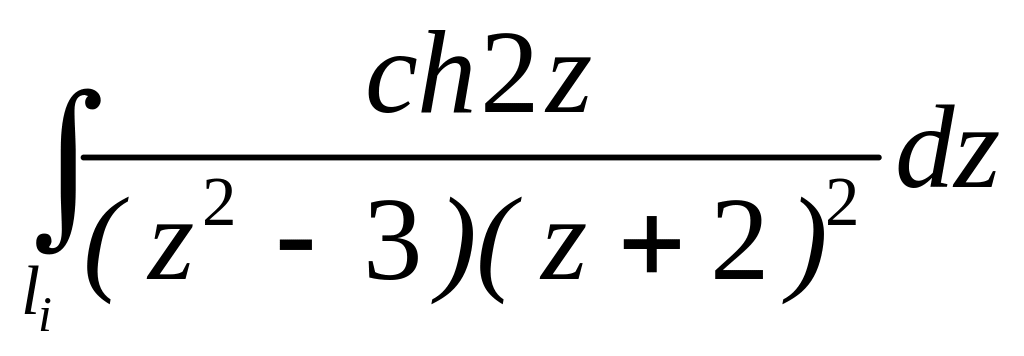 ;
;
;
; 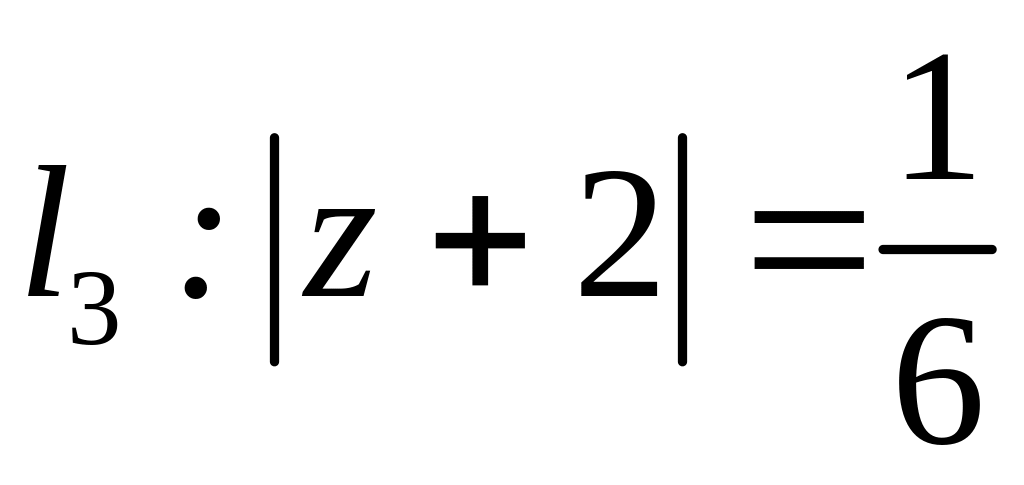 ;
;  .
. ;
;
;
;
;
;  .
.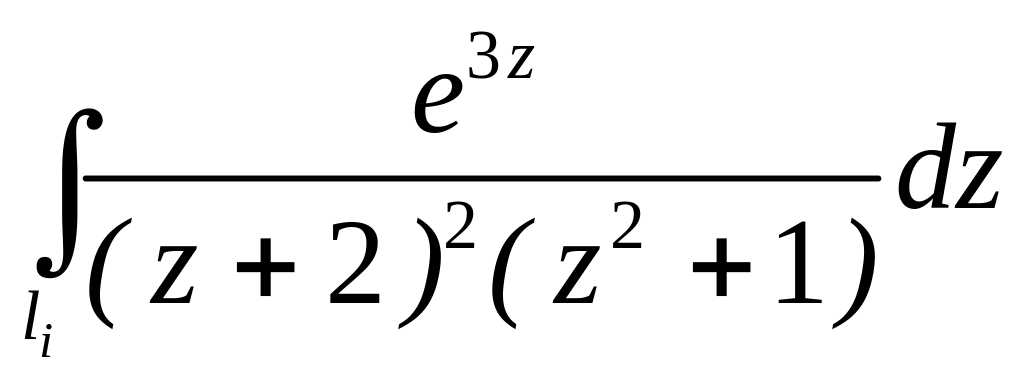 ;
;
;
; 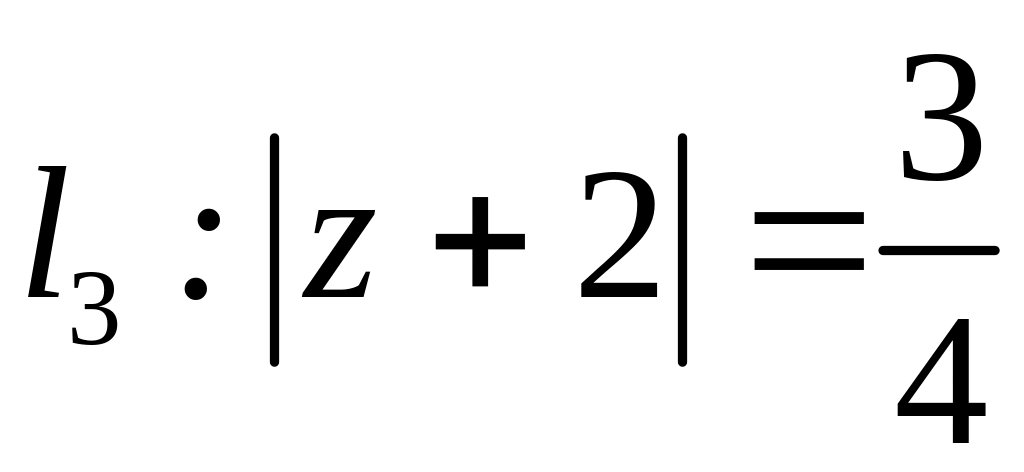 ;
.
;
. ;
;
;
.
;
;
;
.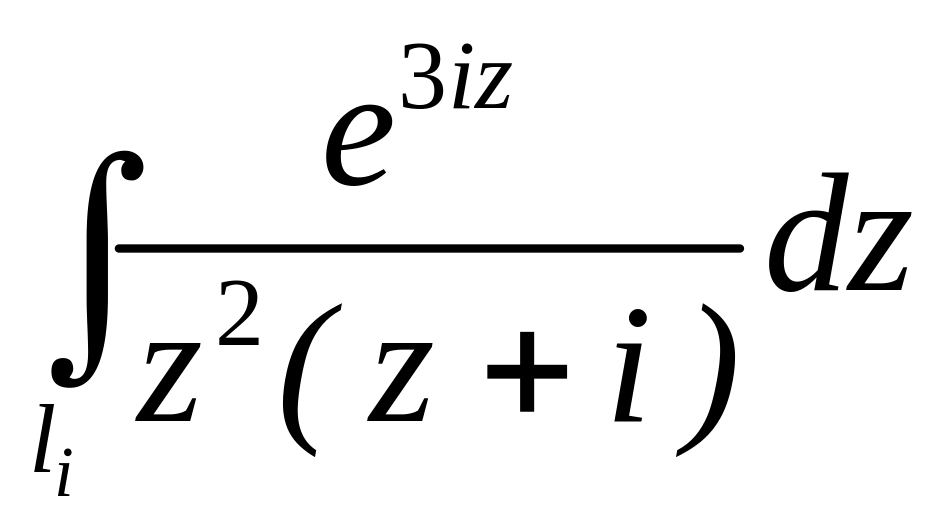 ;
;
;
.
;
;
;
. ;
;
;
;
;
;  .
.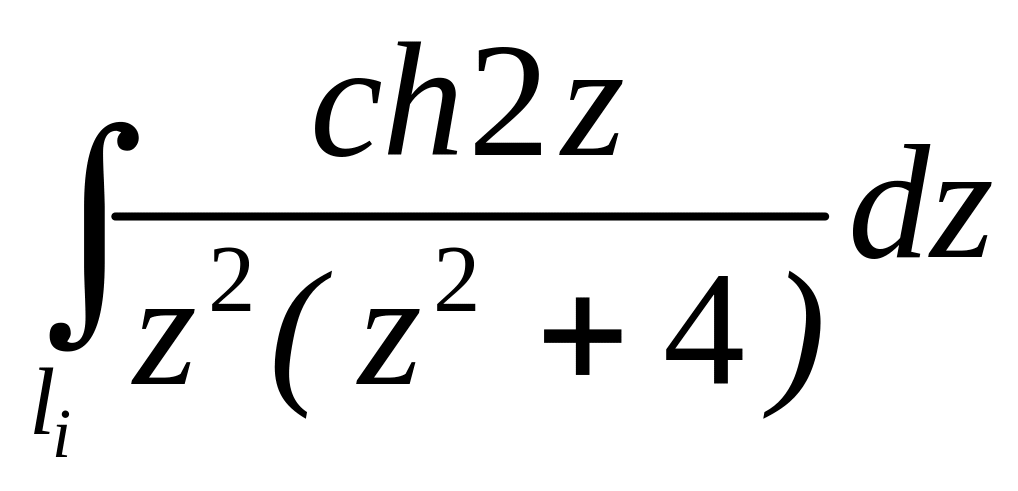 ;
;
;
.
;
;
;
. ;
;
;
;  ;
.
;
.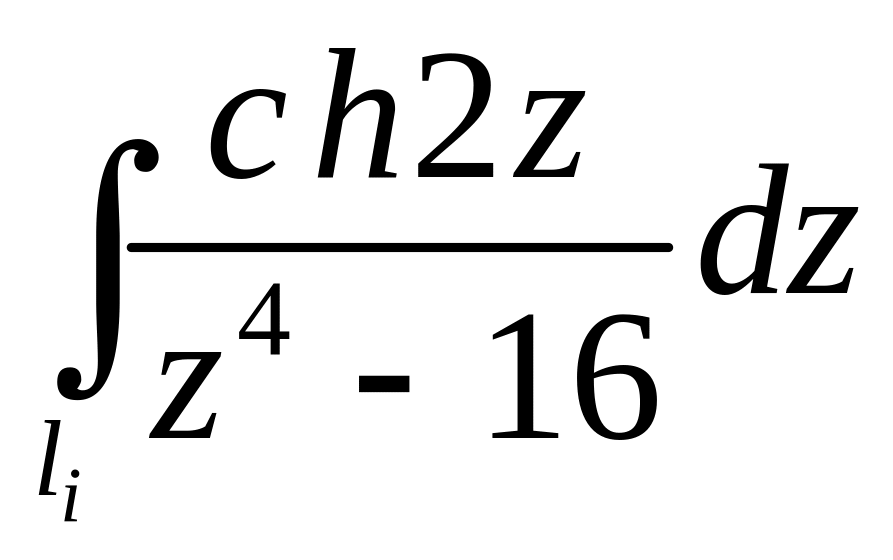 ;
;
;
;
;
; 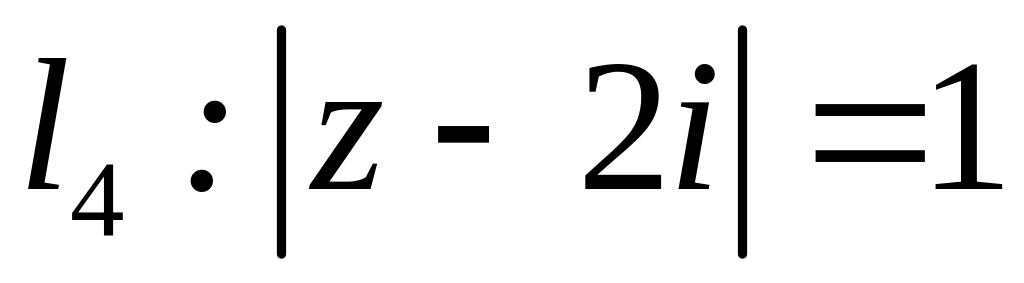 .
.
 ;
;
;
;
;
;  .
.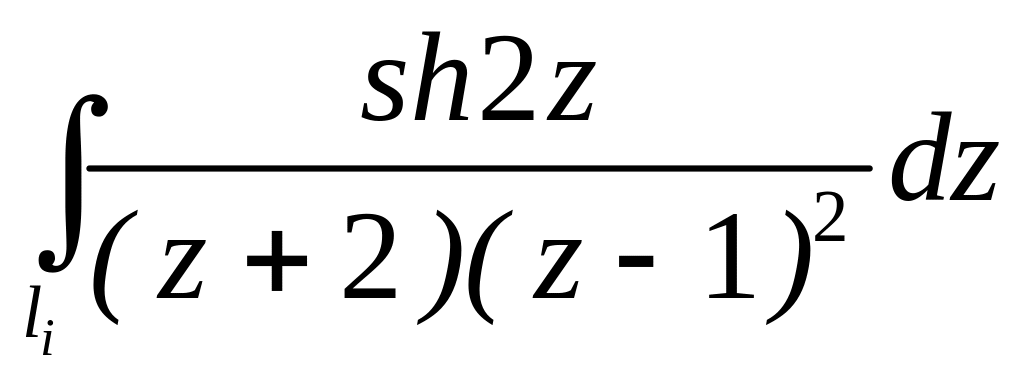
 ;
; 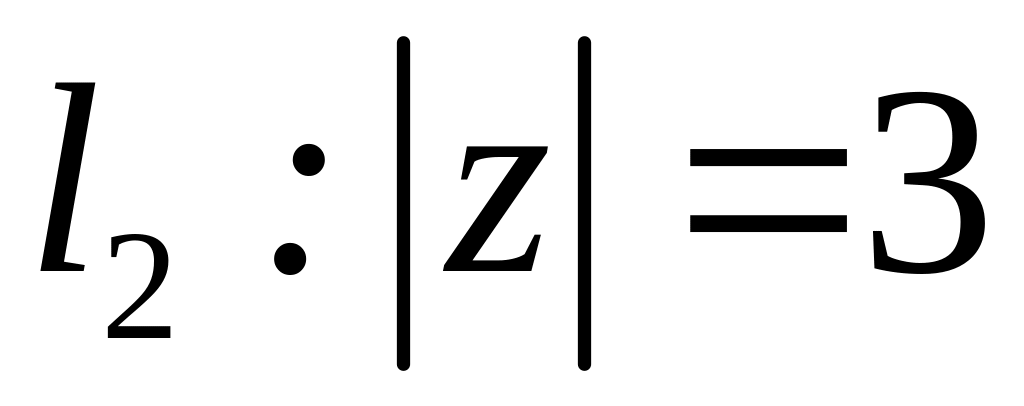 ;
;
;
;  .
.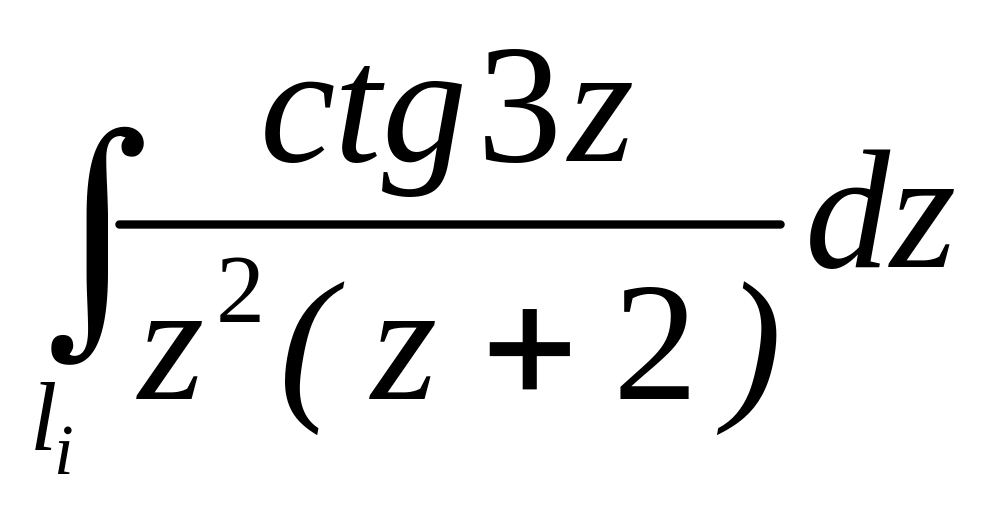 ;
;
;
.
;
;
;
. ;
;  ;
; 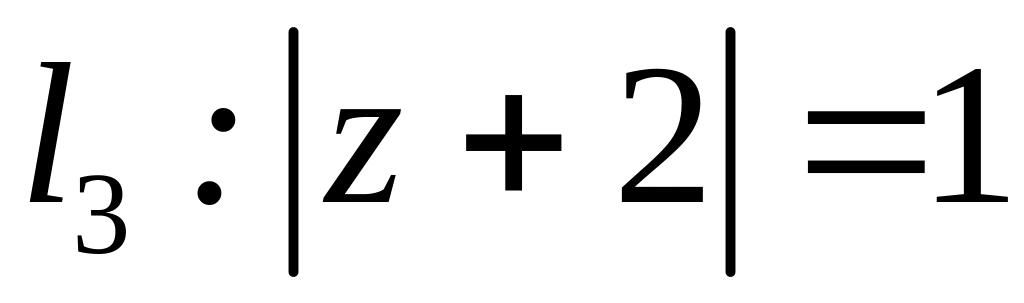 ;
.
;
. ;
; 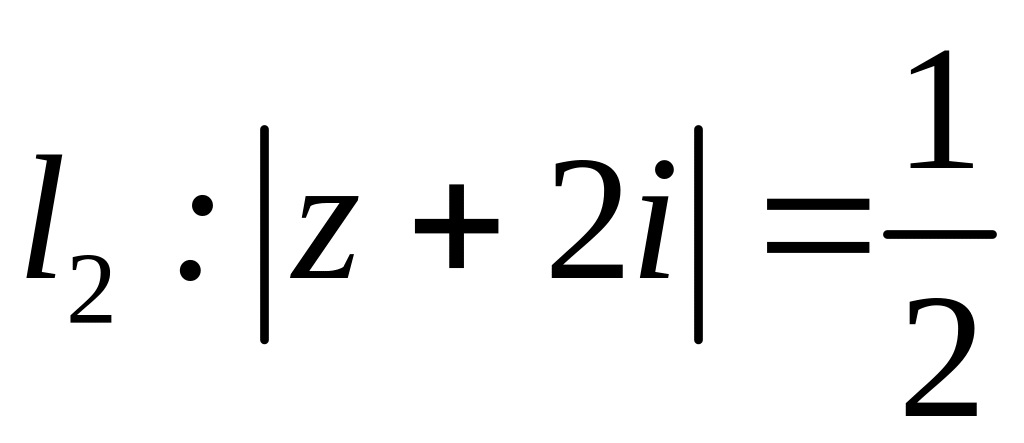 ;
;
.
;
;
. ;
;  ;
;
;
; 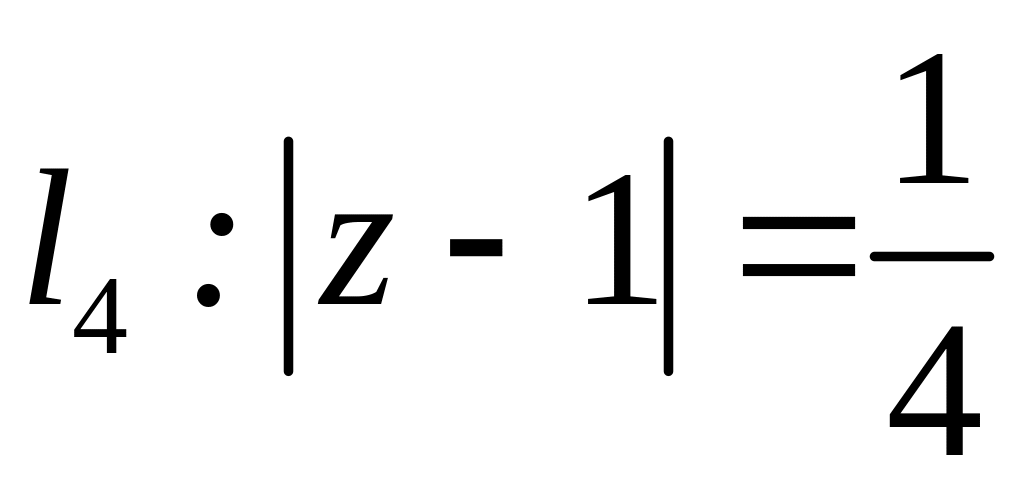 .
. ;
; 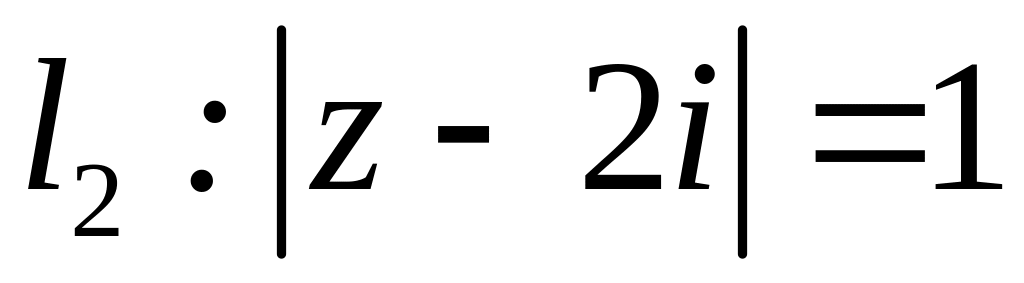 ;
;
.
;
;
.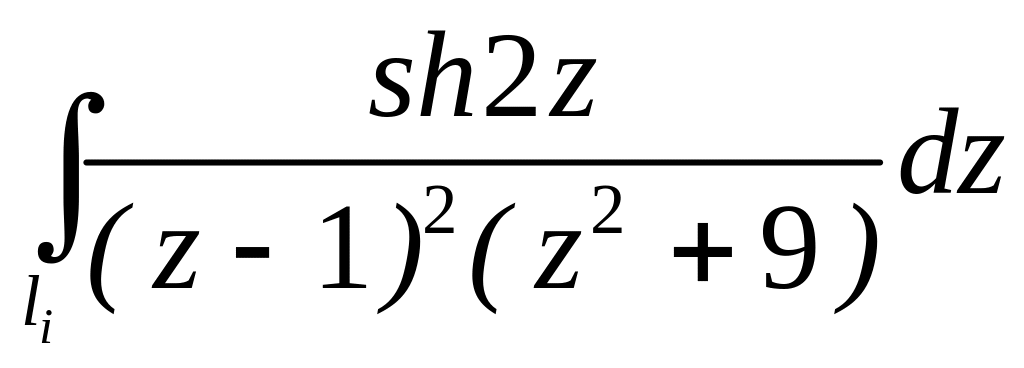 ;
;
;
.
;
;
;
.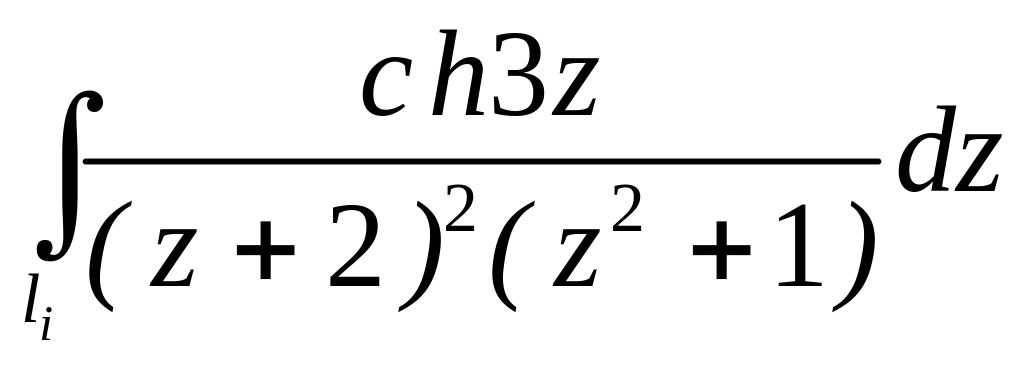 ;
;
;
.
;
;
;
.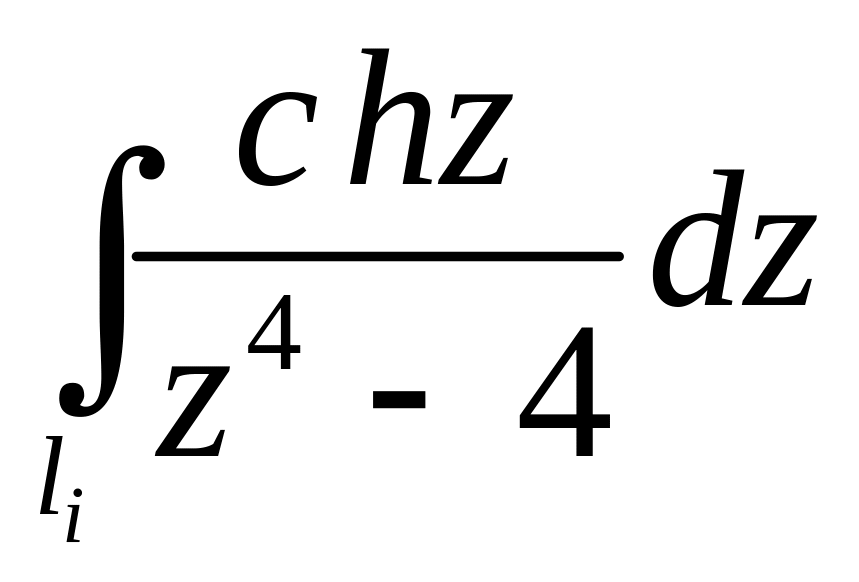 ;
;  ;
;  ;
;  .
.
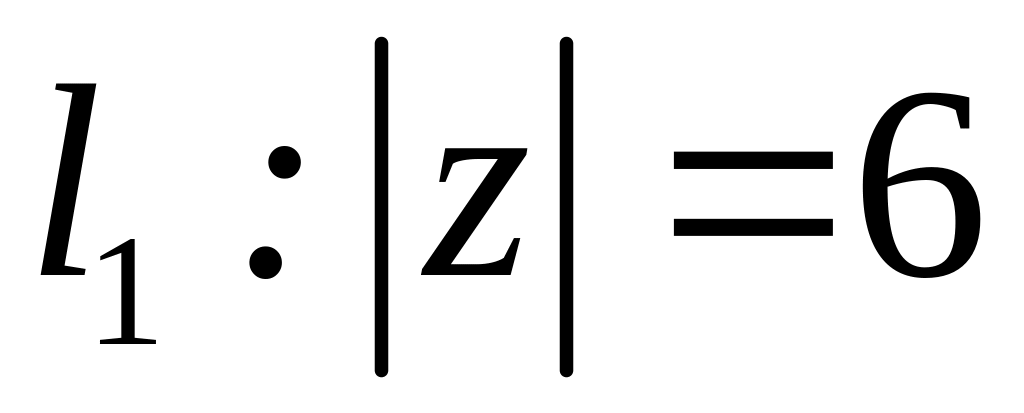 ;
;
;
;
;
; 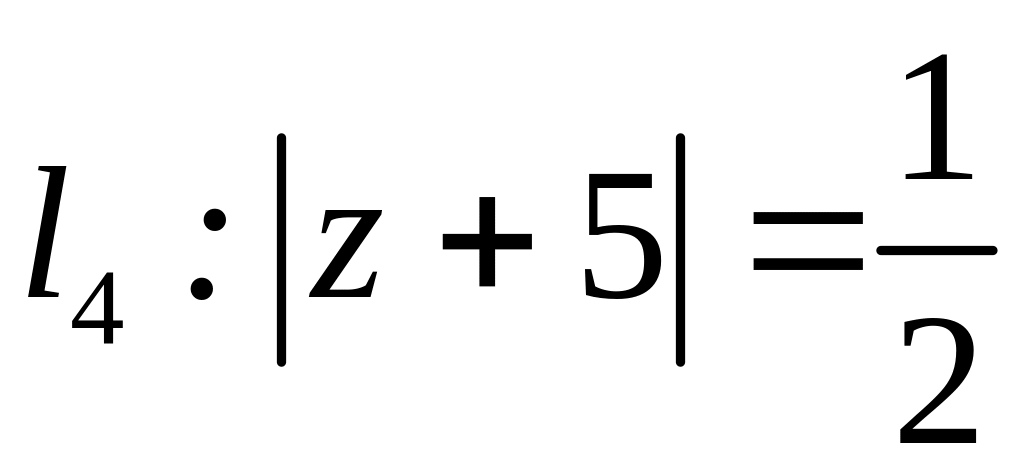 .
. ;
;
;
; 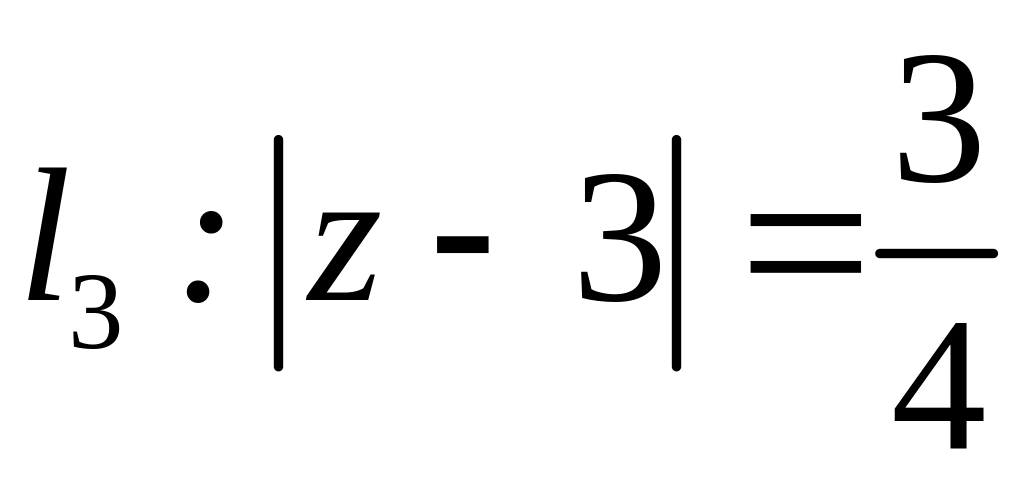 ;
.
;
.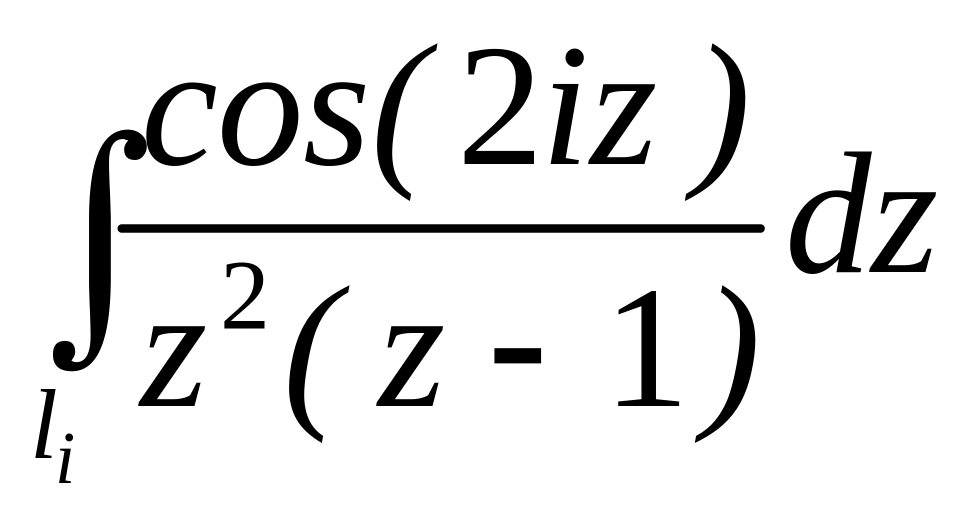 ;
;
;
; 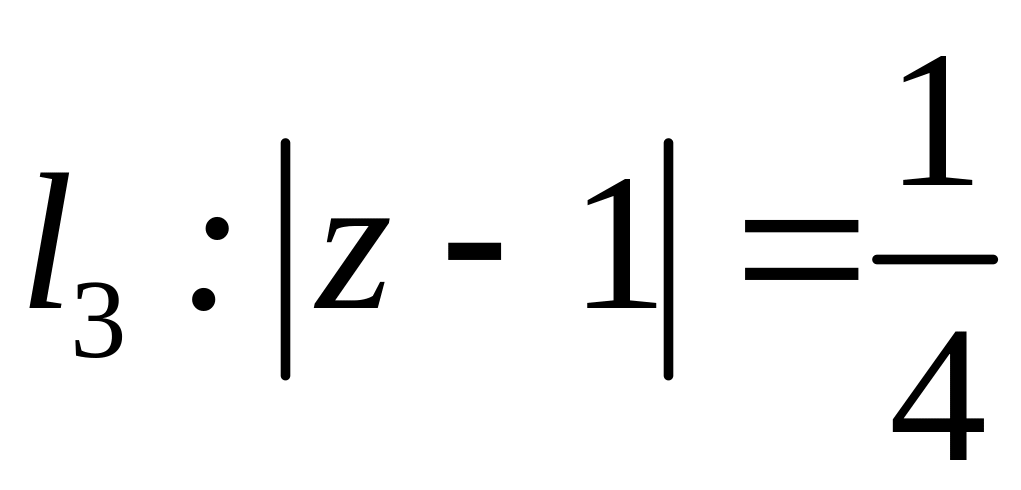 ;
.
;
. ;
;  ;
;
.
;
;
.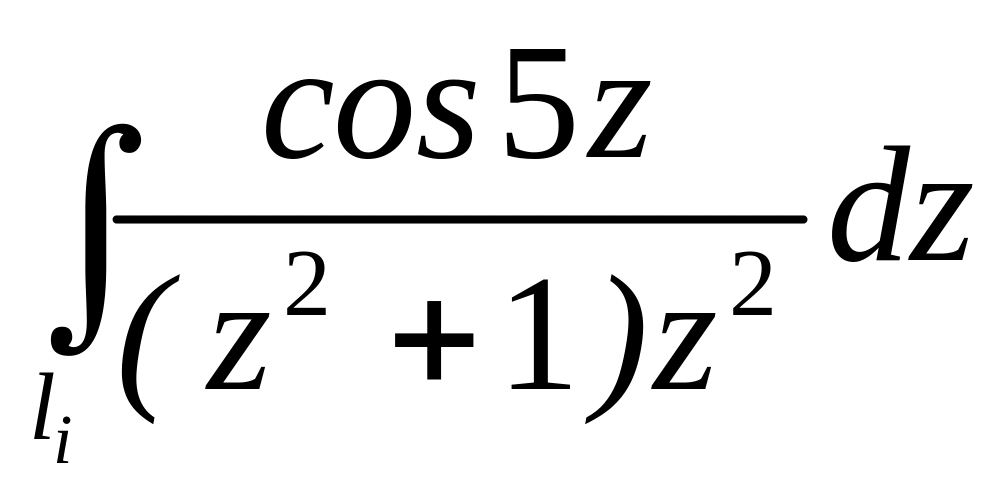 ;
;
;
.
;
;
;
.
4.2.7 Для функцій
![]() та
та
![]() виконати такі дії:
виконати такі дії:
а) розкласти функції в ряд Лорана;
б) визначити характер особливих точок;
в) вказати область збіжності ряду.
 за степенями
за степенями
 ;
; 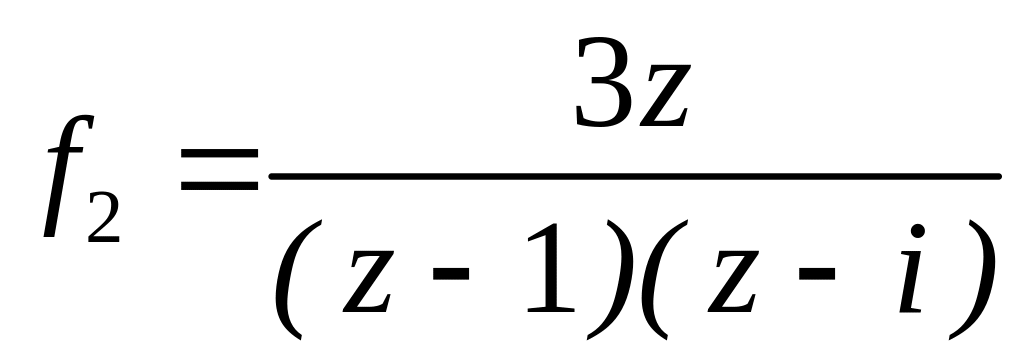 в околі точок
в околі точок
 та
та
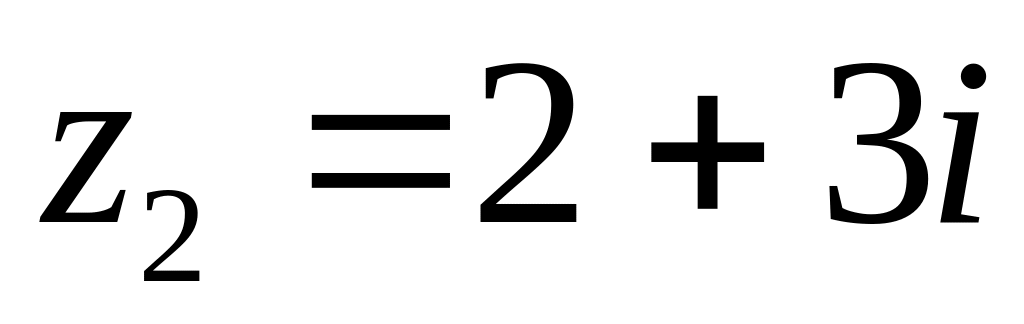 .
.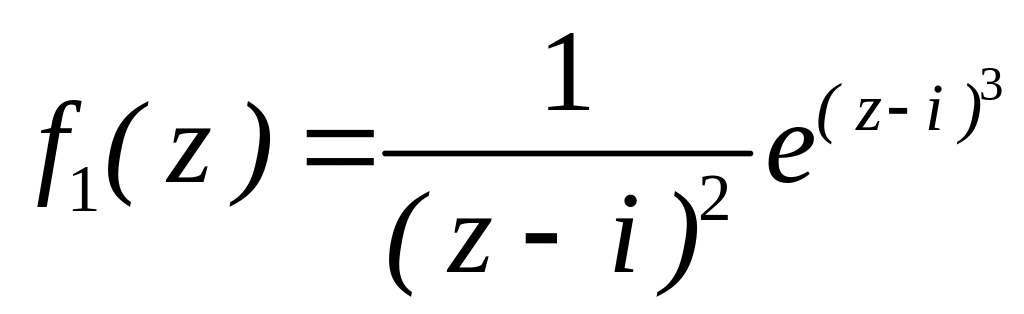 за степенями
за степенями
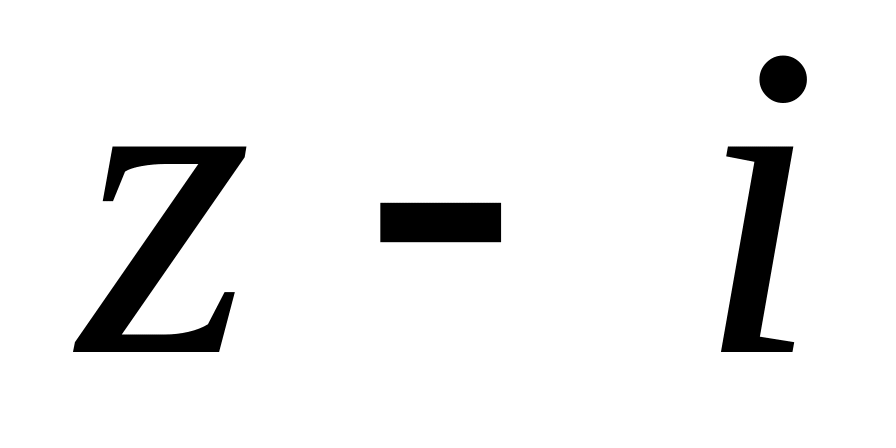 ;
;  в околі точок
в околі точок
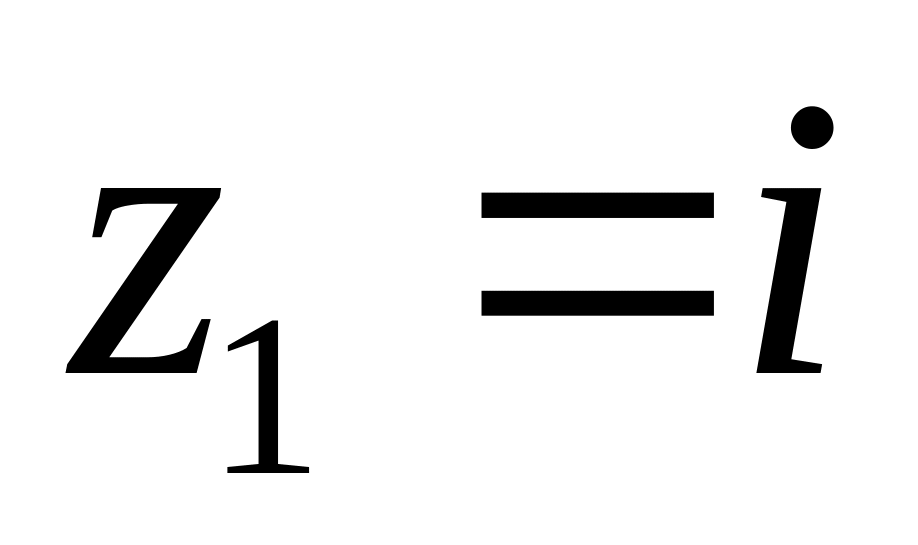 та
та
 .
. за степенями
;
в околі точок
та
за степенями
;
в околі точок
та
 .
.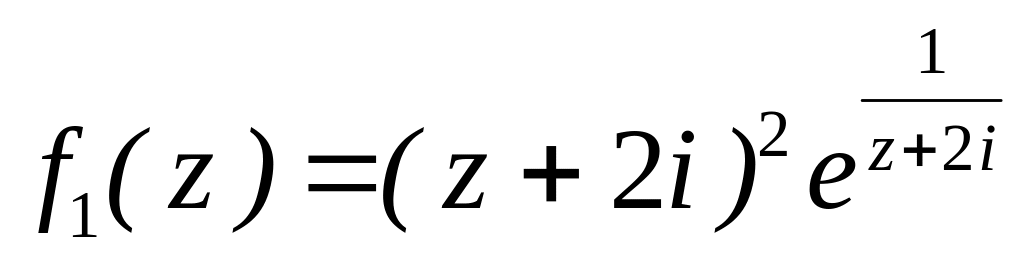 за степенями
за степенями
 ;
;  в околі точок
в околі точок
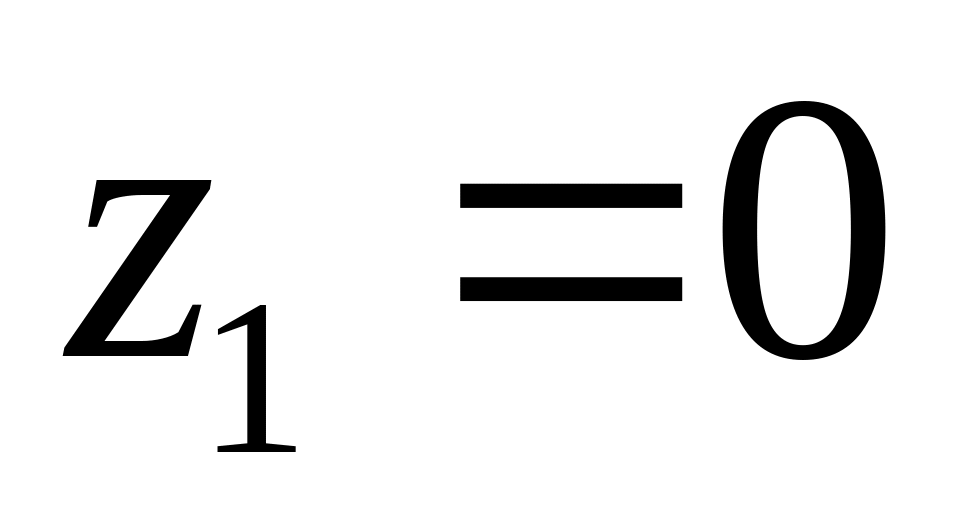 та
та
 .
.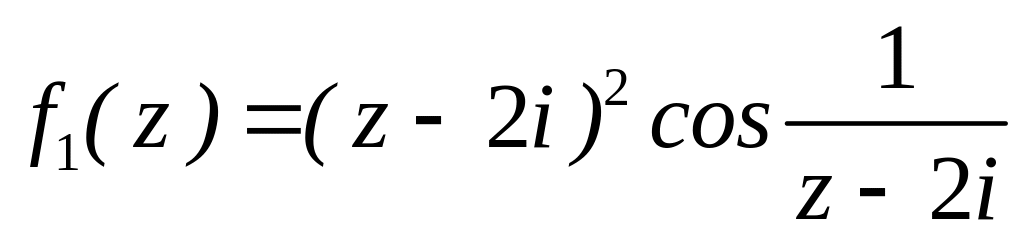 за степенями
за степенями
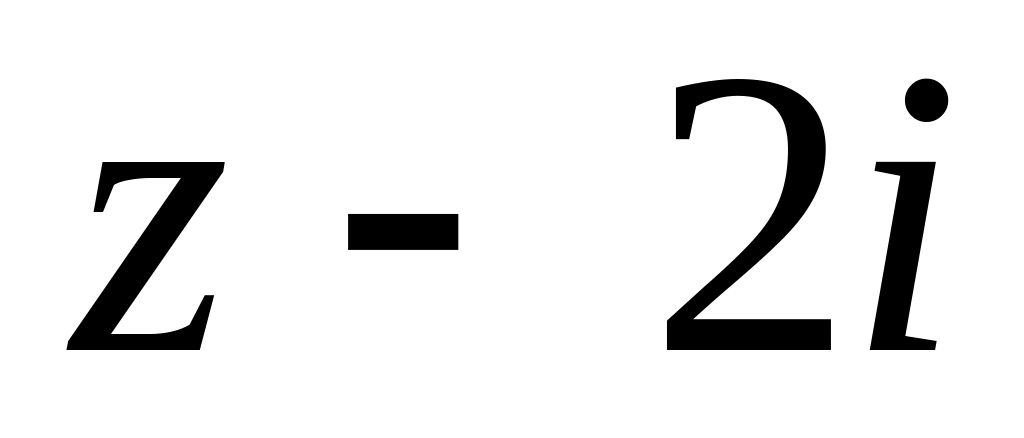 ;
; 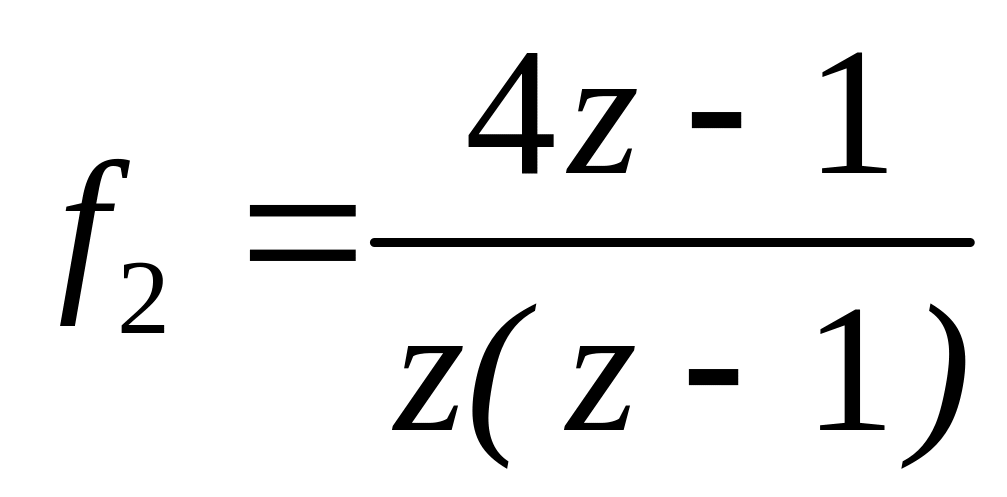 в околі точок
та
в околі точок
та
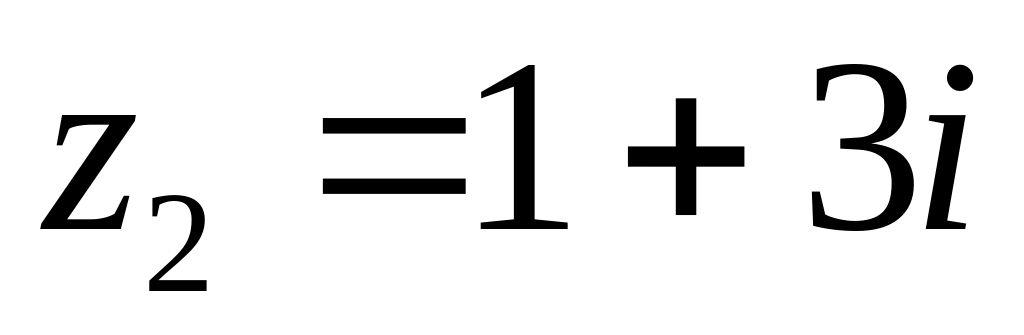 .
. за степенями
;
за степенями
; 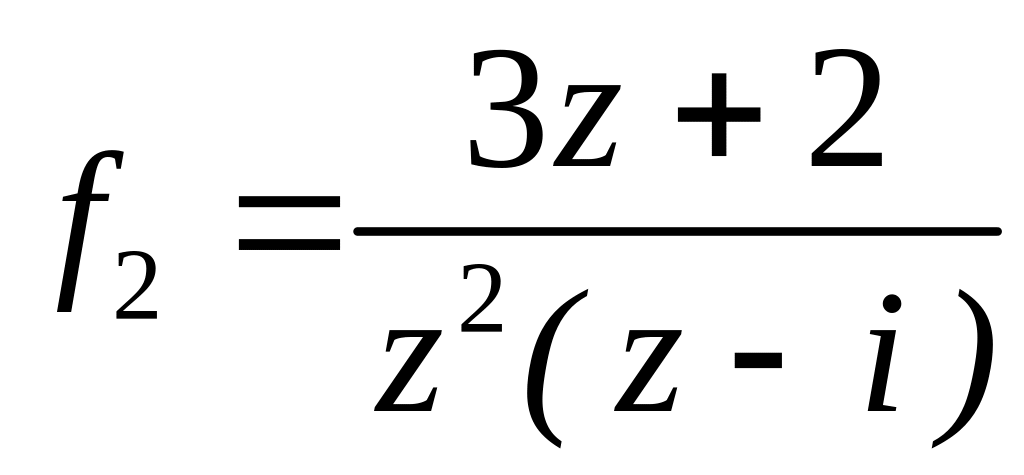 в околі точок
та
в околі точок
та
 .
. за степенями
за степенями
 ;
; 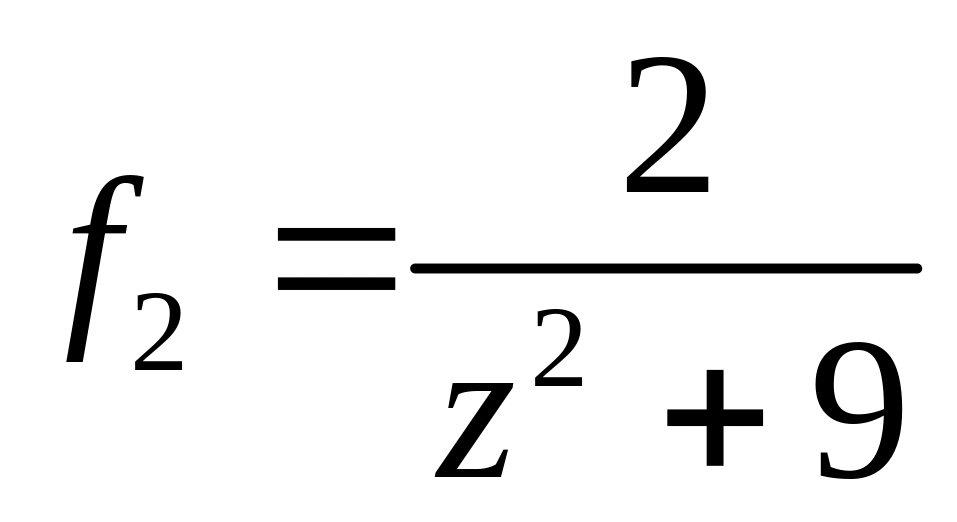 в околі точок
в околі точок
 та
та
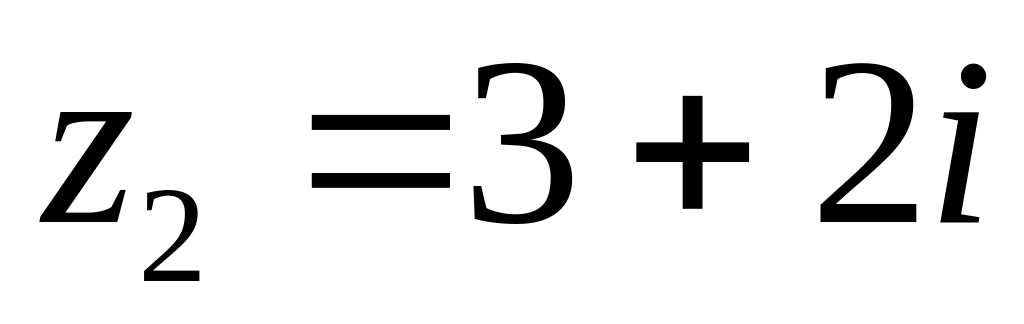 .
.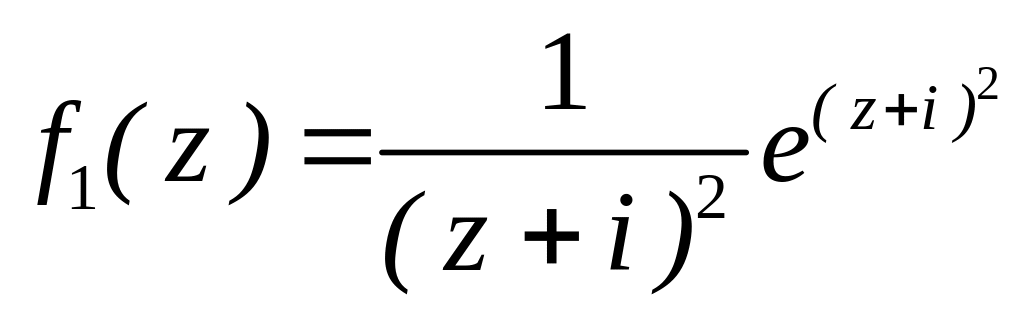 за степенями
;
за степенями
;  в околі точок
та
в околі точок
та
 .
.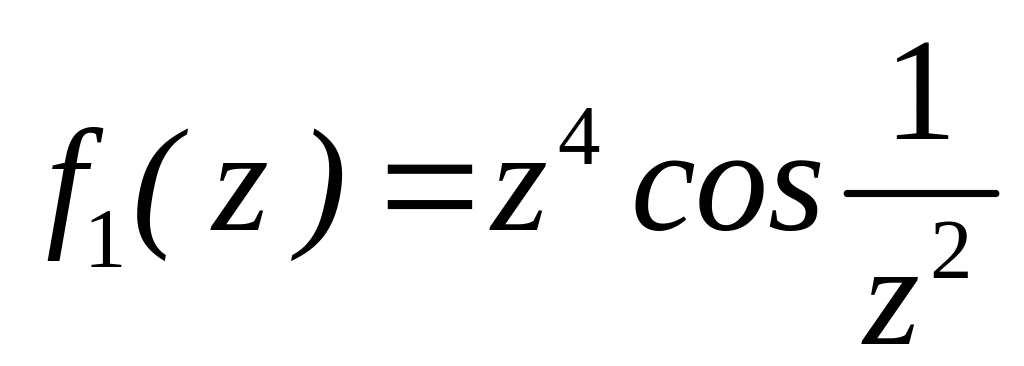 за степенями
;
за степенями
; 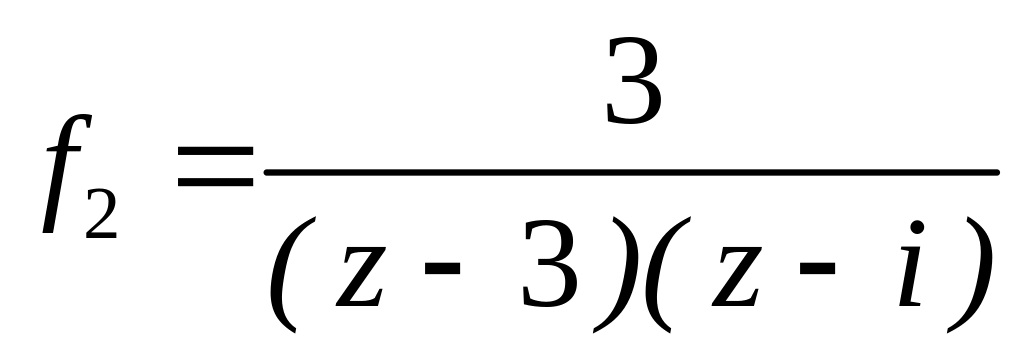 в околі точок
та
.
в околі точок
та
.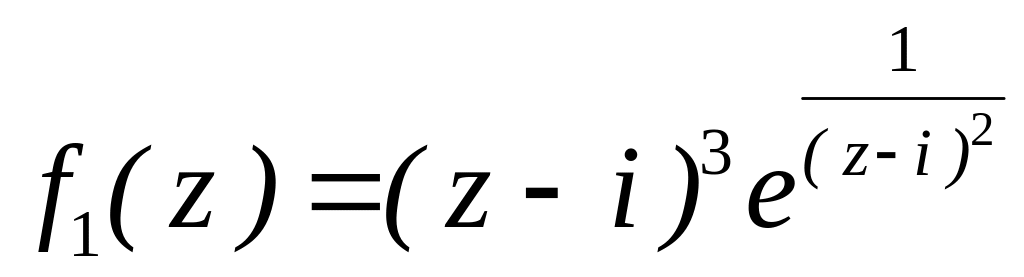 за степенями
;
за степенями
;  в околі точок
в околі точок
 та
.
та
. за степенями
;
за степенями
; 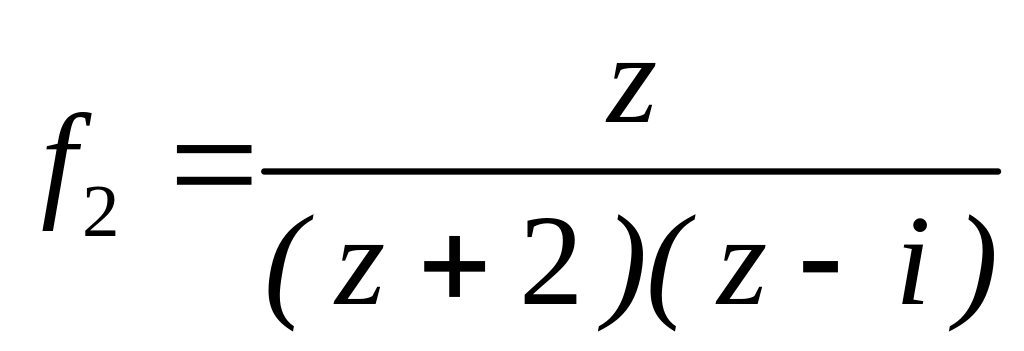 в околі точок
в околі точок
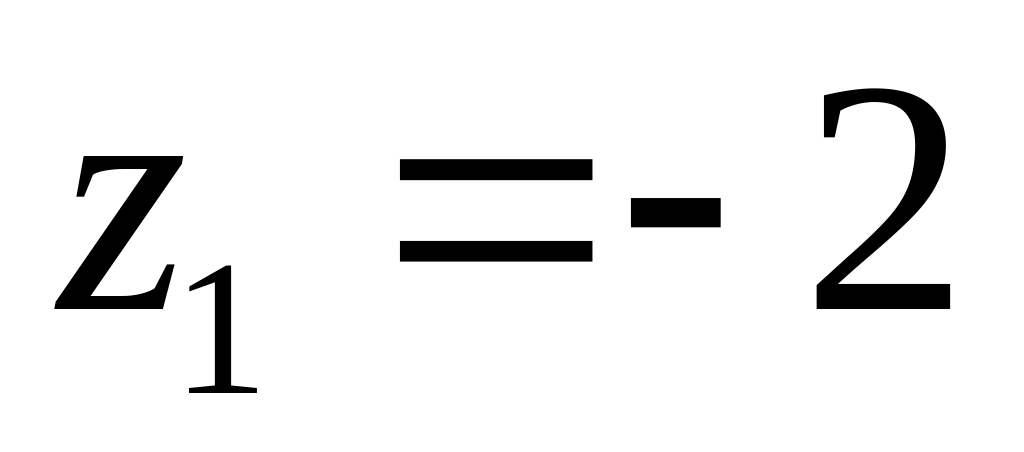 та
.
та
.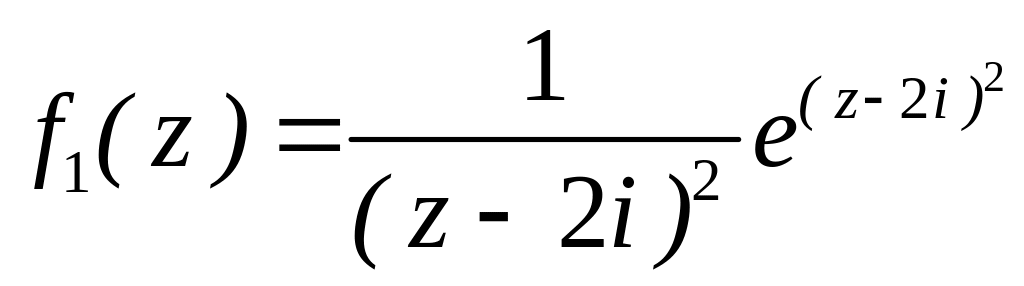 за степенями
;
за степенями
;  в околі точок
в околі точок
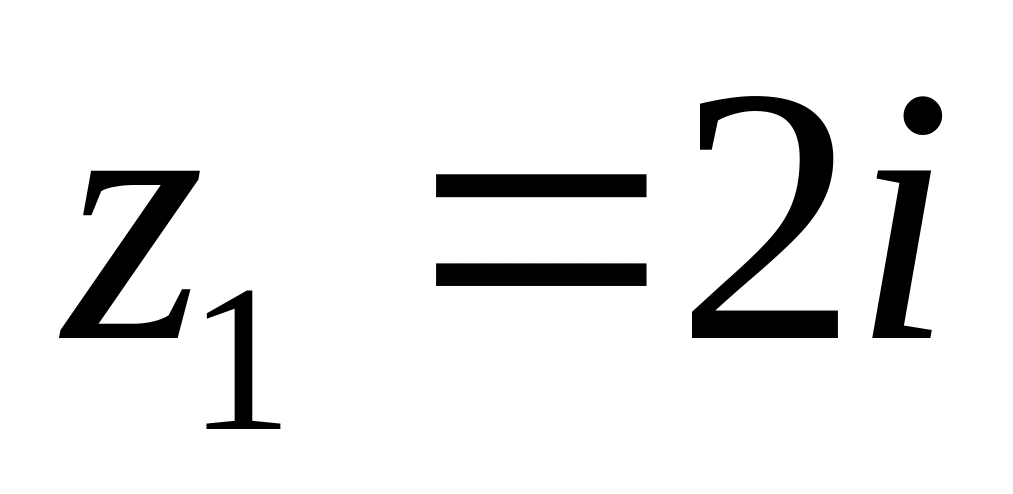 та
.
та
. за степенями
за степенями
 ;
; 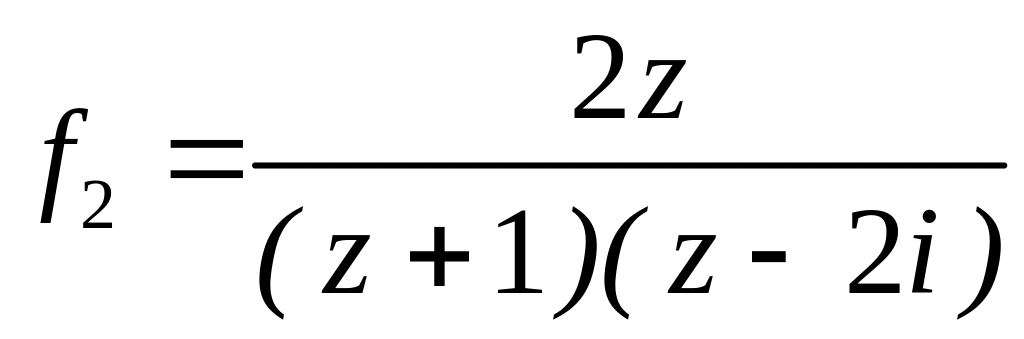 в околі точок
в околі точок
 та
та
 .
.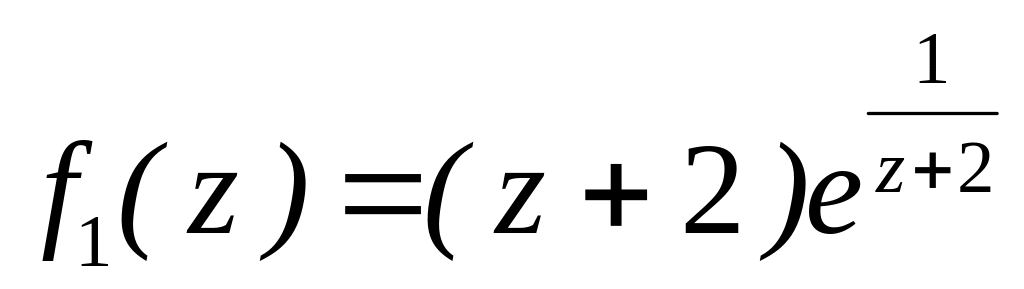 за степенями
за степенями
 ;
;  в околі точок
та
.
в околі точок
та
. за степенями
;
за степенями
; 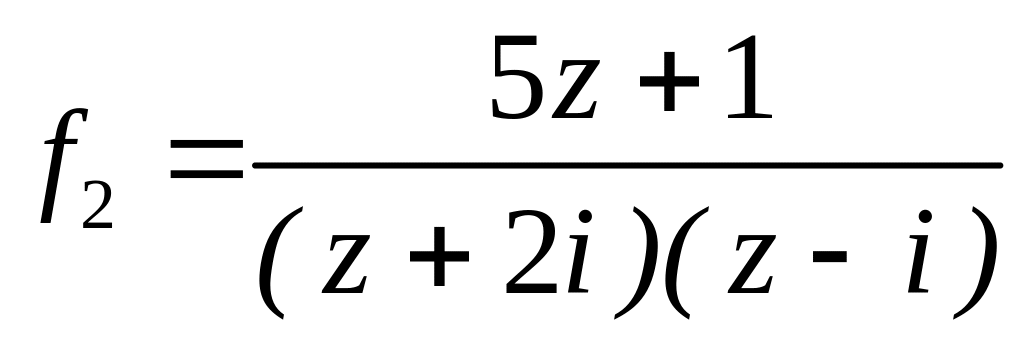 в околі точок
та
в околі точок
та
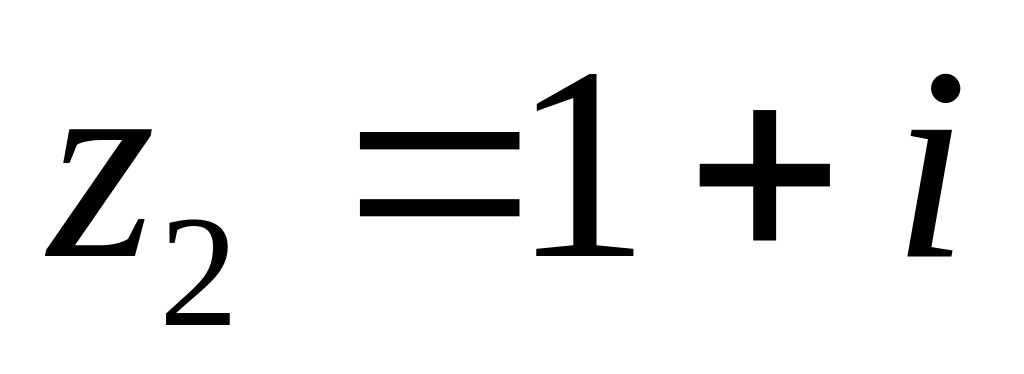 .
.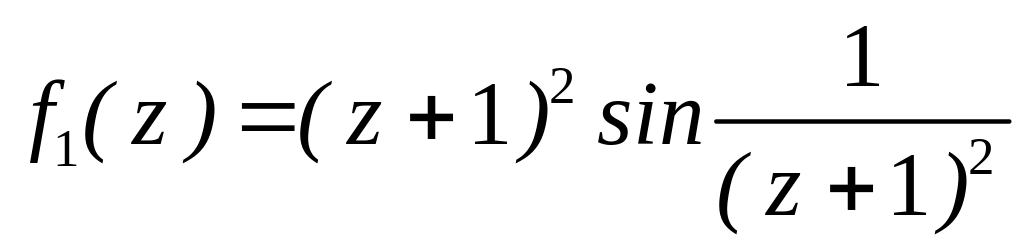 за степенями
за степенями
 ;
; 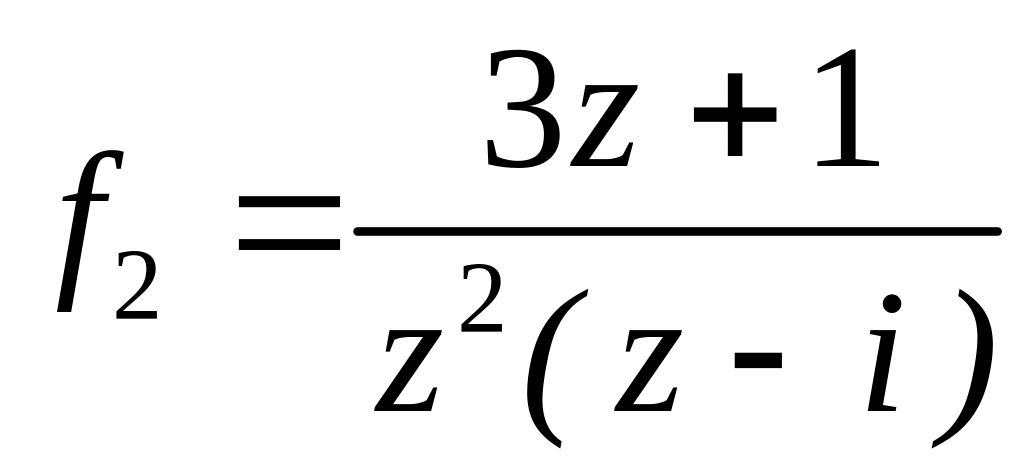 в околі точок
та
.
в околі точок
та
.за степенями ;
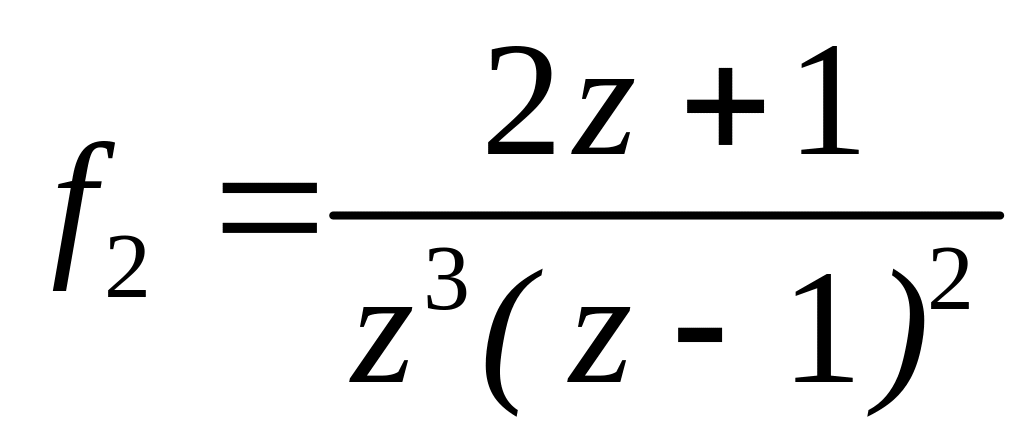 в околі точок
та
.
в околі точок
та
. за степенями
;
за степенями
;  в околі точок
та
.
в околі точок
та
. за степенями
;
за степенями
;  в околі точок
в околі точок
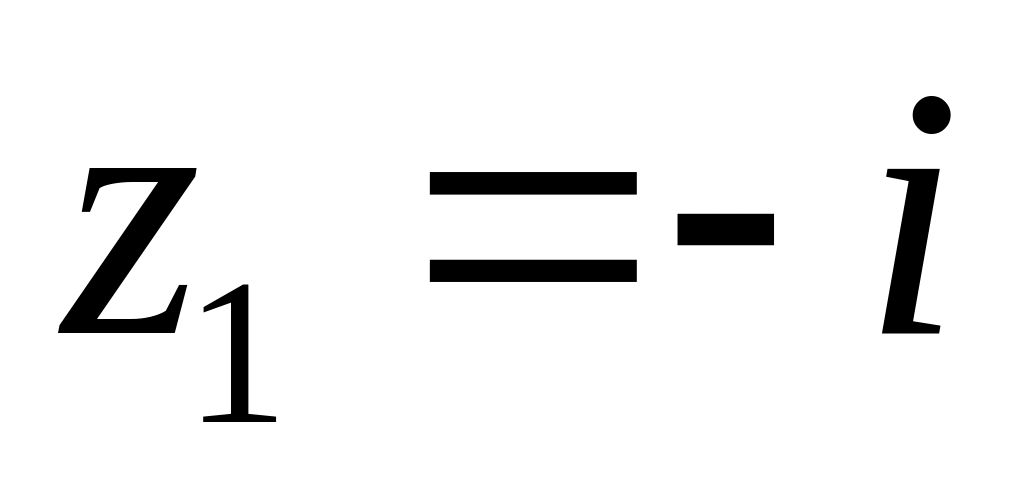 та
.
та
.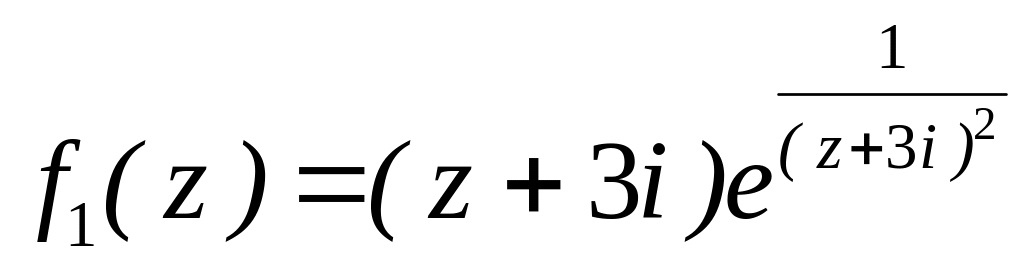 за степенями
за степенями
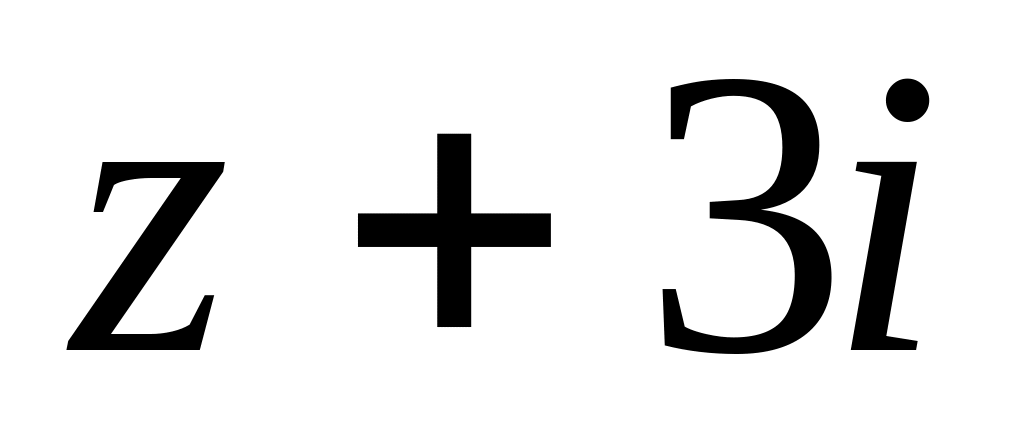 ;
в околі точок
та
.
;
в околі точок
та
.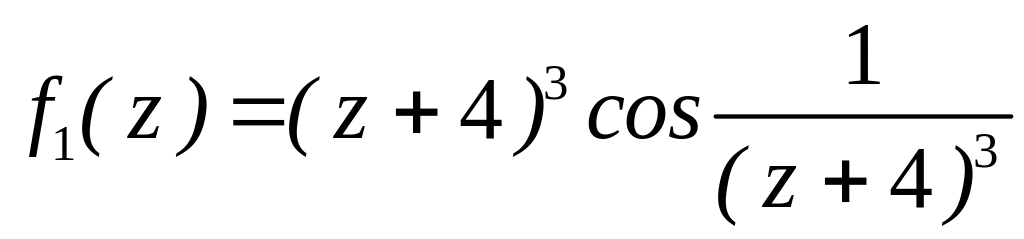 за степенями
за степенями
 ;
;  в околі точок
та
в околі точок
та
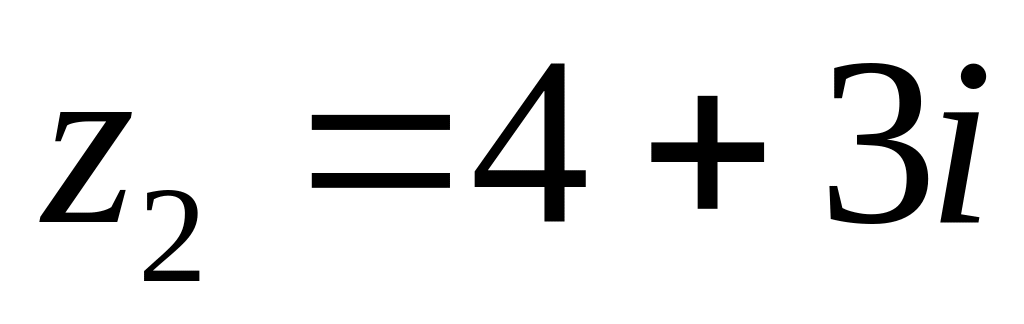 .
.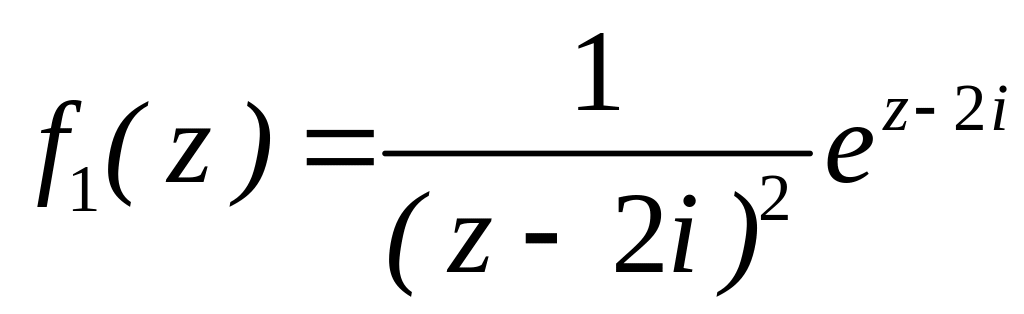 за степенями
;
за степенями
; 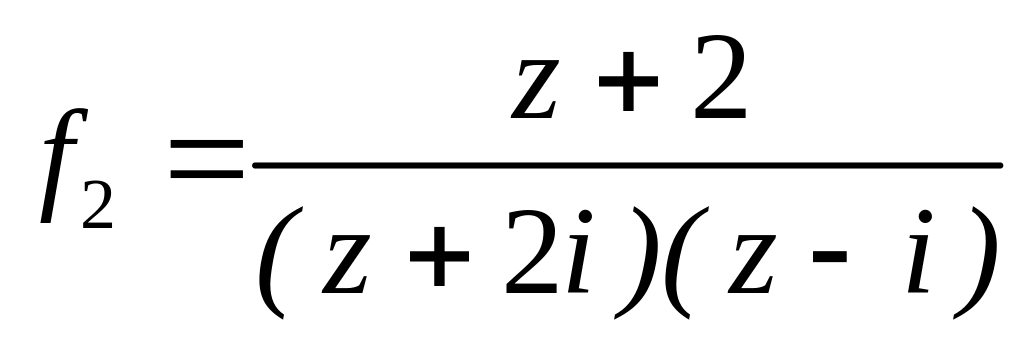 в околі точок
та
.
в околі точок
та
. за степенями
за степенями
 ;
;  в околі точок
та
в околі точок
та
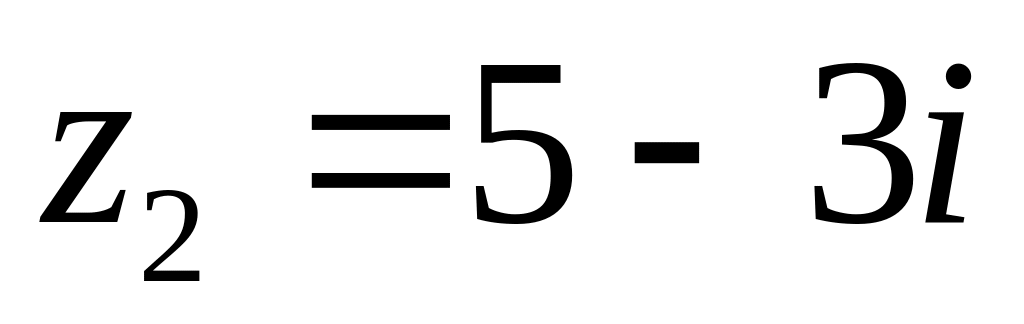 .
.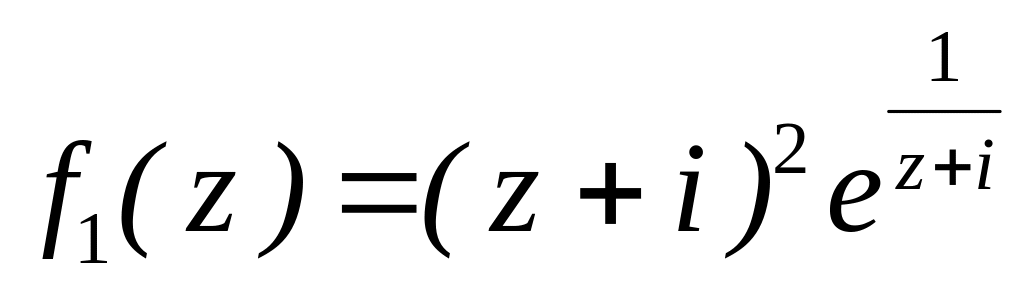 за степенями
;
за степенями
;  в околі точок
та
в околі точок
та
 .
. за степенями
;
за степенями
; 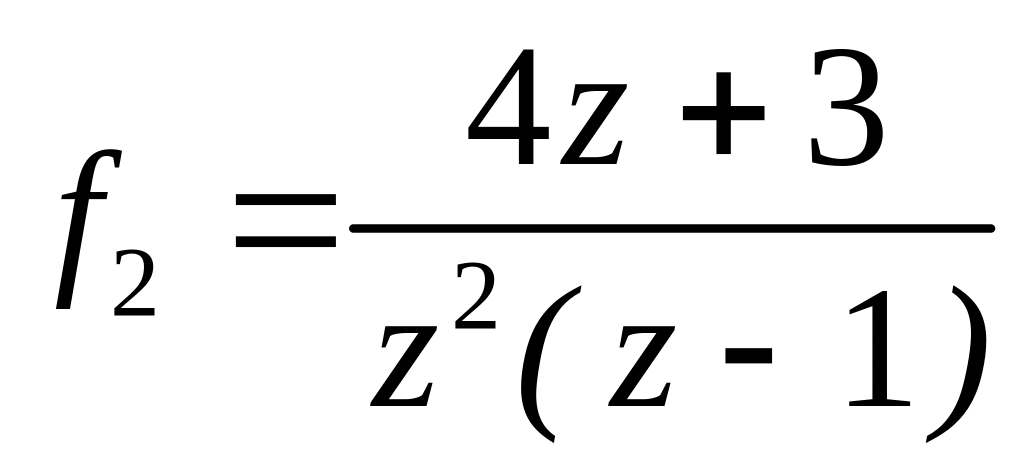 в околі точок
та
.
в околі точок
та
.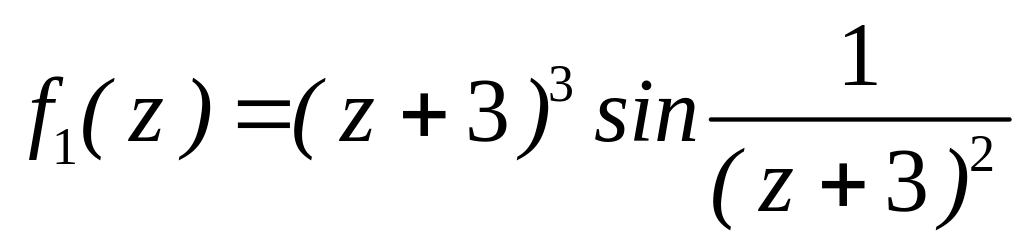 за степенями
за степенями
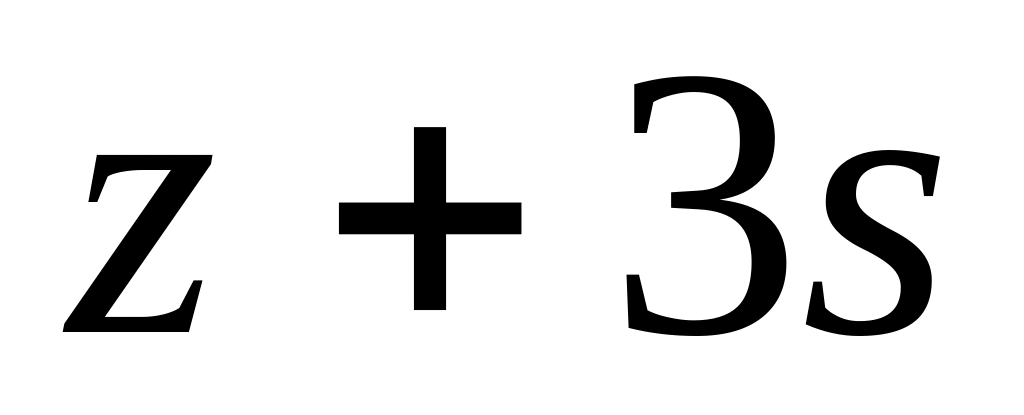 ;
;  в околі точок
та
в околі точок
та
 .
.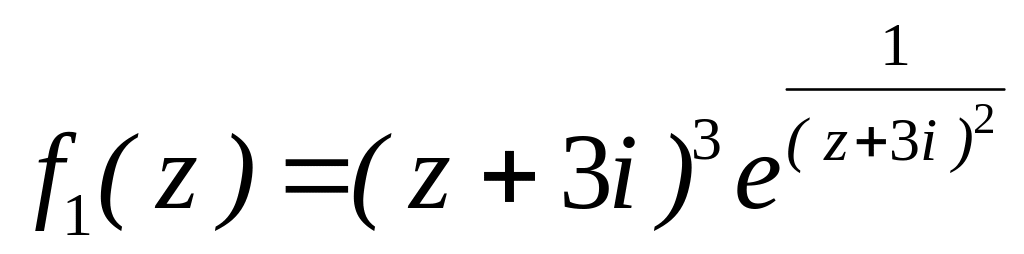 за степенями
;
за степенями
;  в околі точок
в околі точок
 та
та
 .
.за степенями ;
 в околі точок
та
в околі точок
та
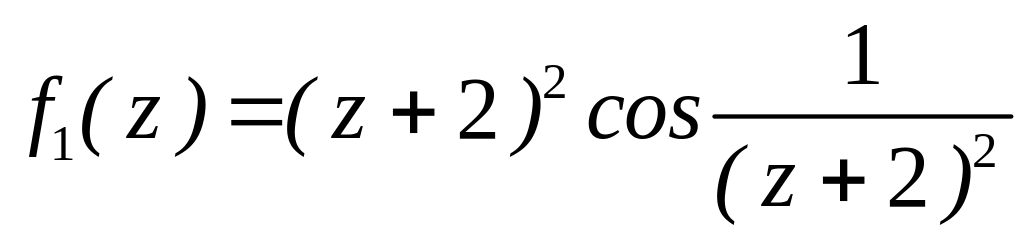 за степенями
;
за степенями
;  в околі точок
та
в околі точок
та
 за степенями
;
за степенями
; 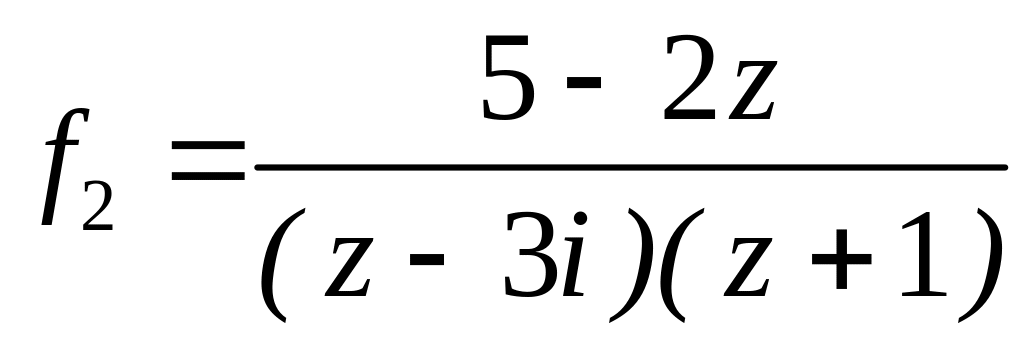 в околі точок
в околі точок
 та
та
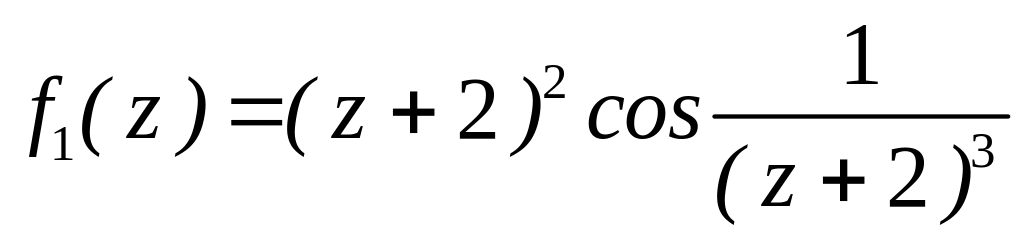 за степенями
;
за степенями
; 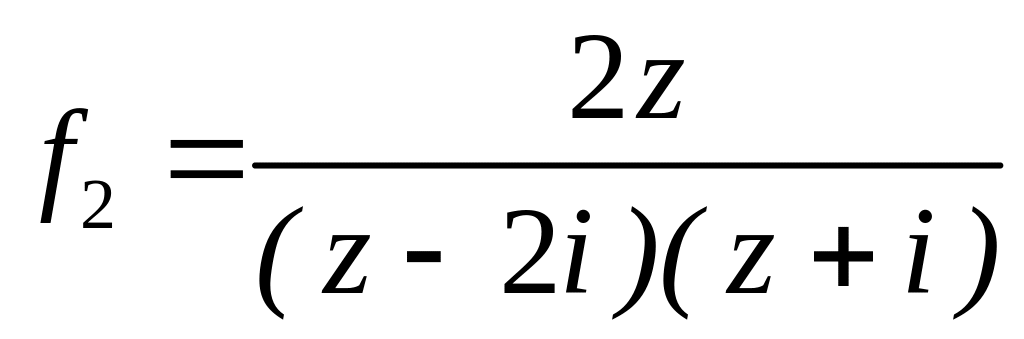 в околі точок
та
в околі точок
та
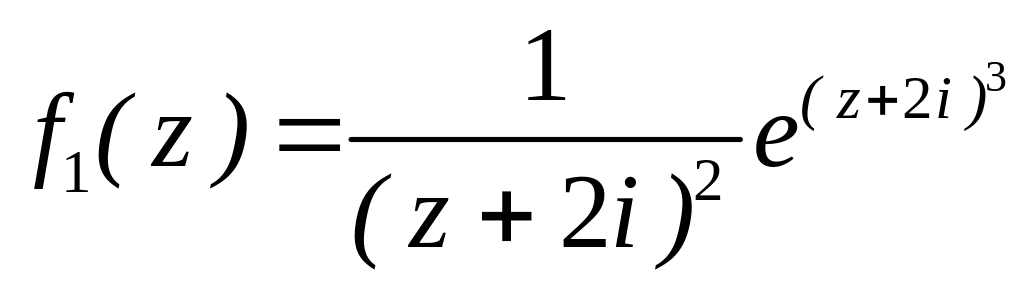 за степенями
;
за степенями
;  в околі точок
та
в околі точок
та
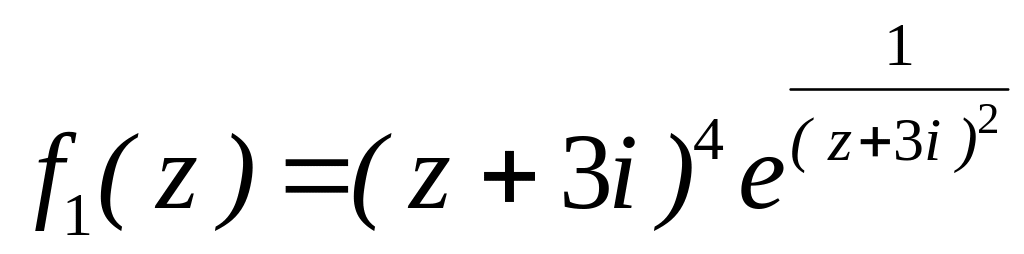 за степенями
;
за степенями
; 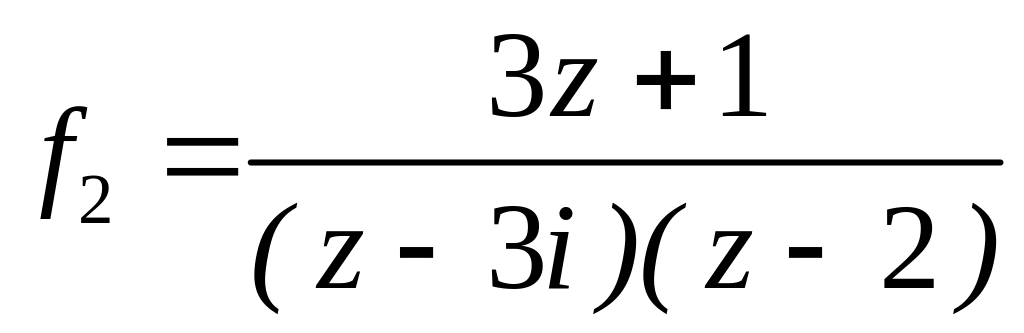 в околі точок
та
в околі точок
та

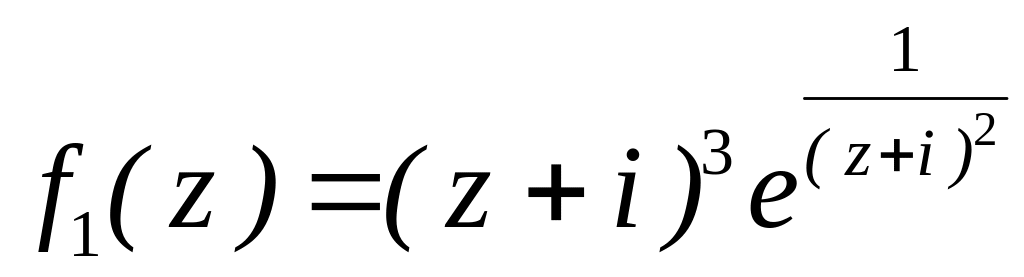 за степенями
;
за степенями
;  в околі точок
та
в околі точок
та
 за степенями
;
за степенями
; 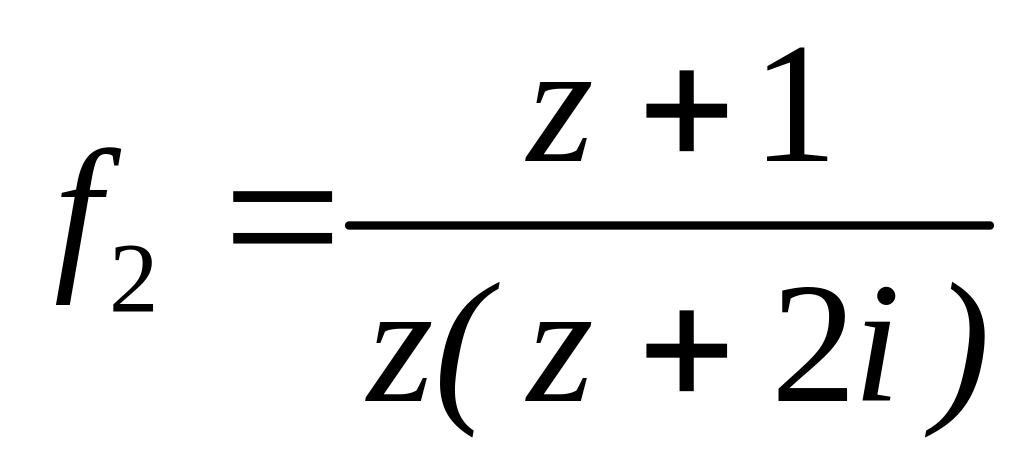 в околі точок
в околі точок
 та
та
 за степенями
;
за степенями
; 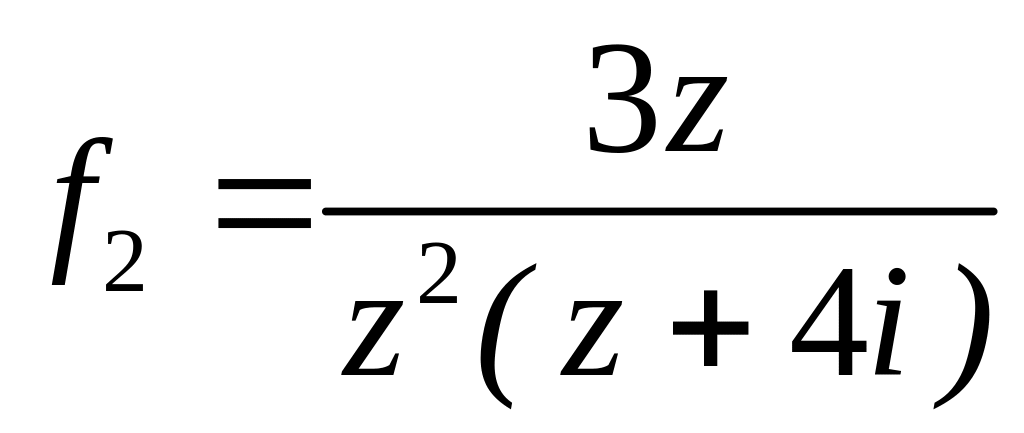 в околі точок
та
в околі точок
та
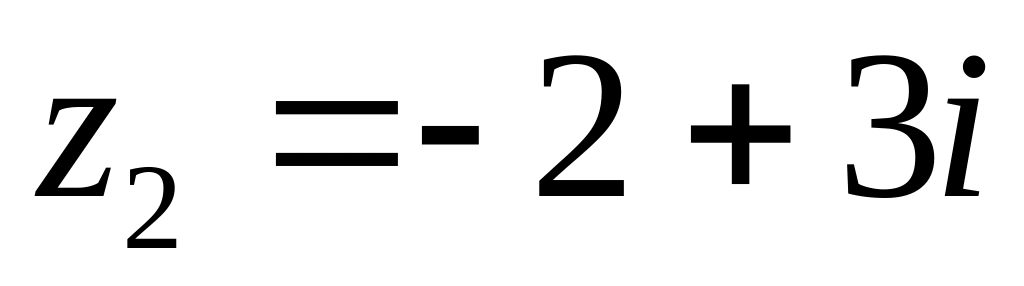
за степенями ;
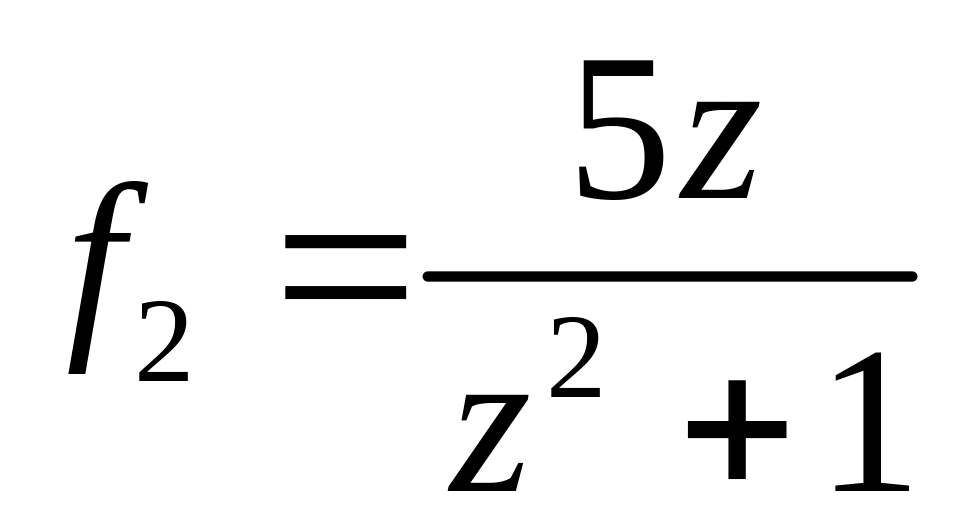 в околі точок
та
в околі точок
та
за степенями ;
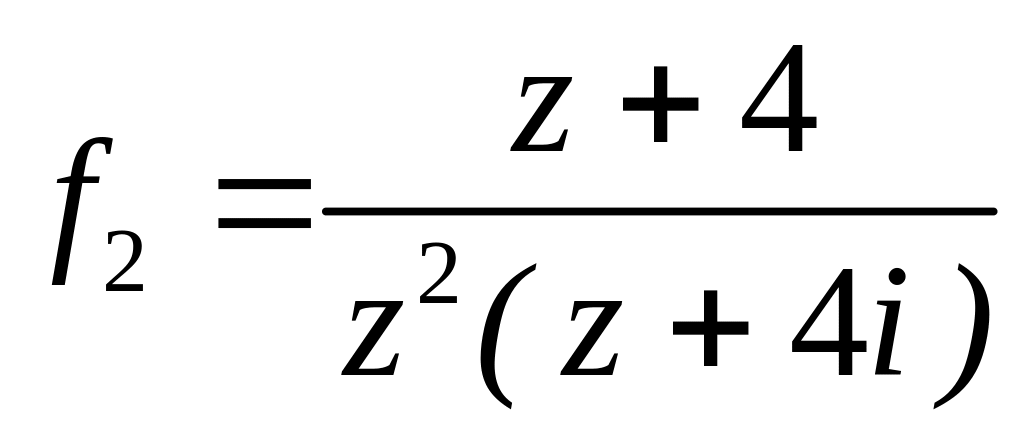 в околі точок
та
в околі точок
та
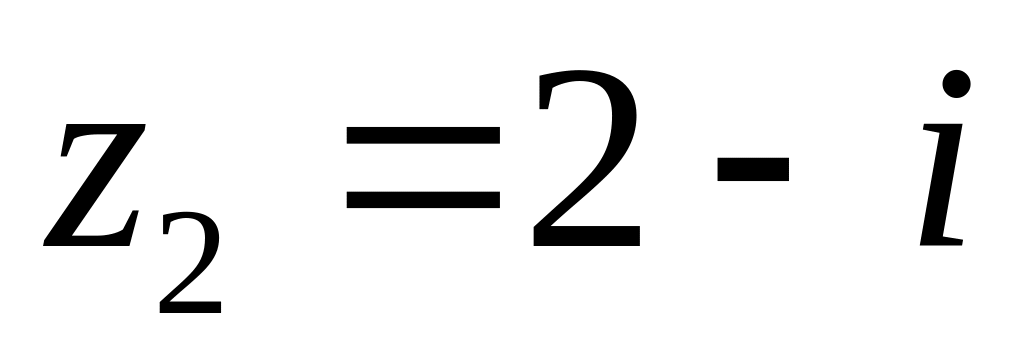
 за степенями
;
за степенями
;  в околі точок
та
в околі точок
та
за степенями ;
 в околі точок
та
в околі точок
та
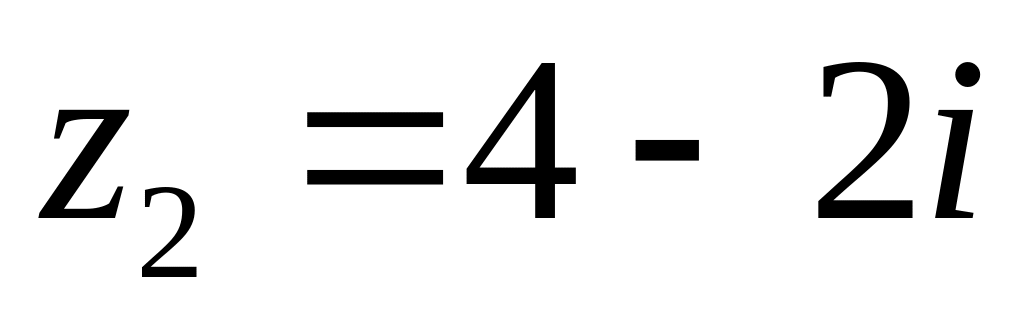
за степенями ;
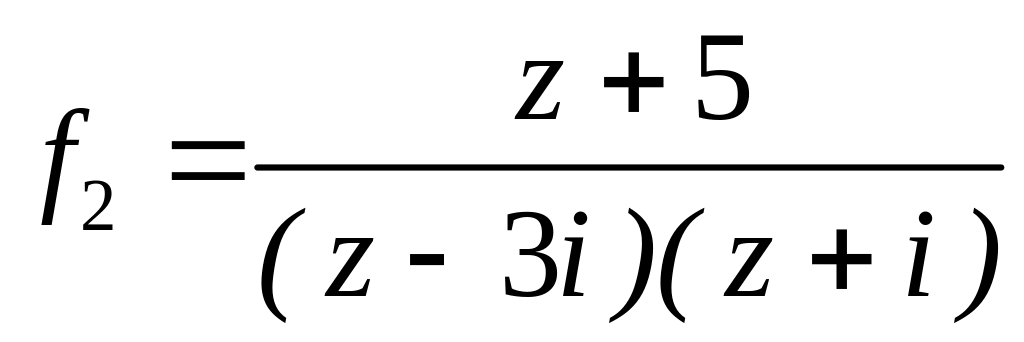 в околі точок
та
в околі точок
та
 за степенями
;
за степенями
;  в околі точок
та
в околі точок
та
 за степенями
за степенями
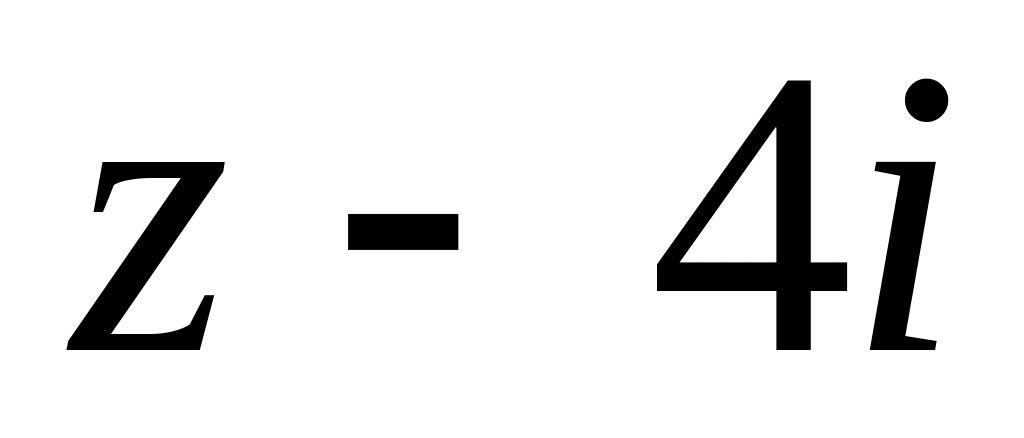 ;
;  в околі точок
та
в околі точок
та

 за степенями
за степенями
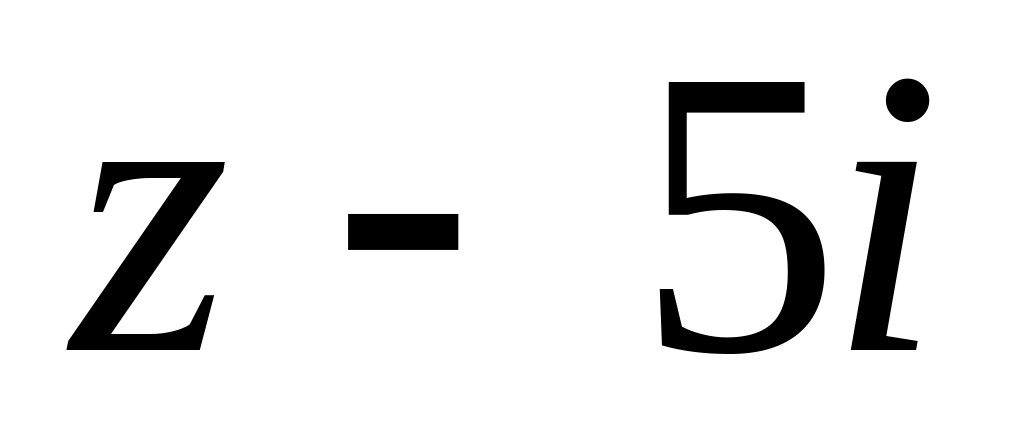 ;
; 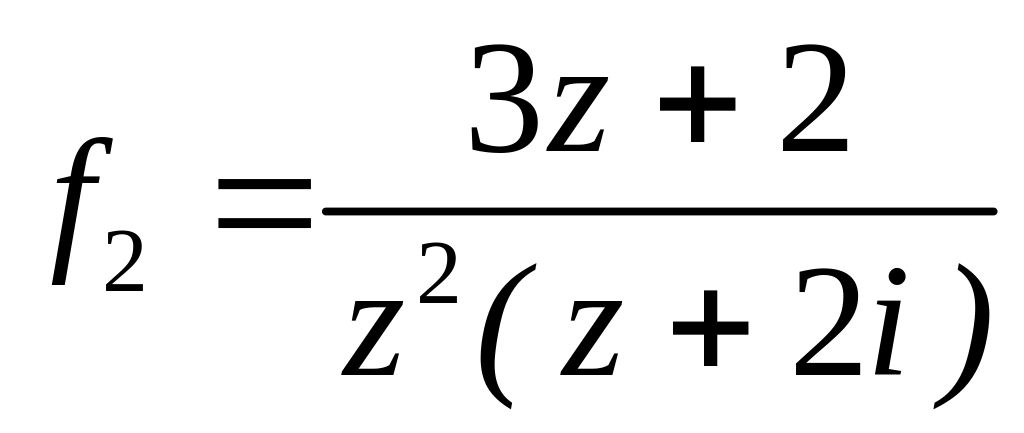 в околі точок
та
в околі точок
та
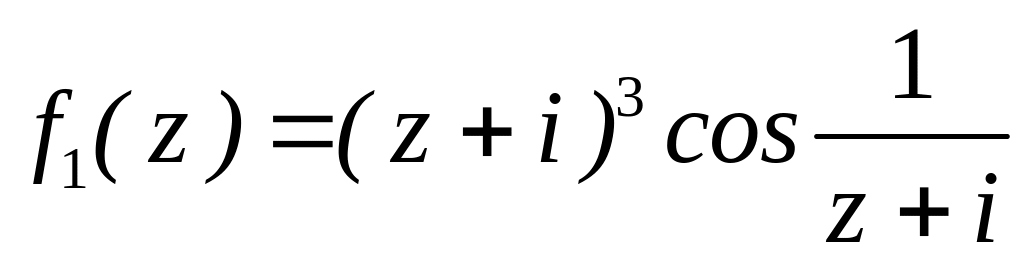 за степенями
;
за степенями
;  в околі точок
та
в околі точок
та
 за степенями
;
за степенями
;  в околі точок
та
в околі точок
та
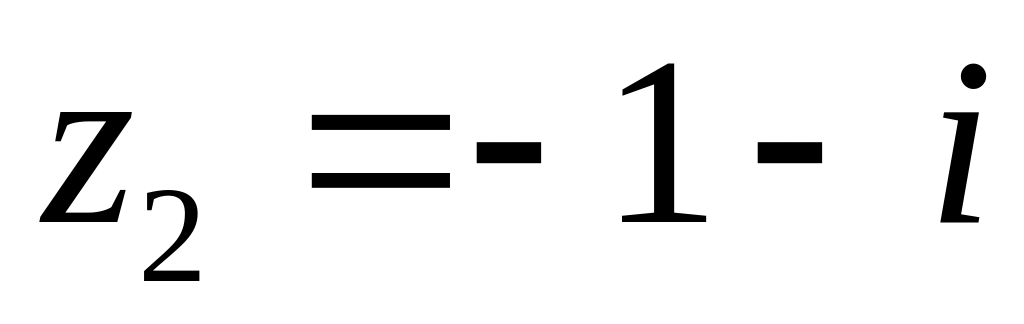
за степенями ;
 в околі точок
в околі точок
 та
та
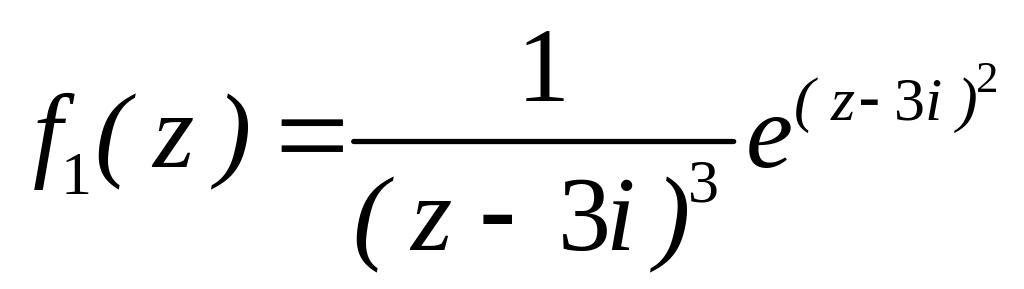 за степенями
;
за степенями
; 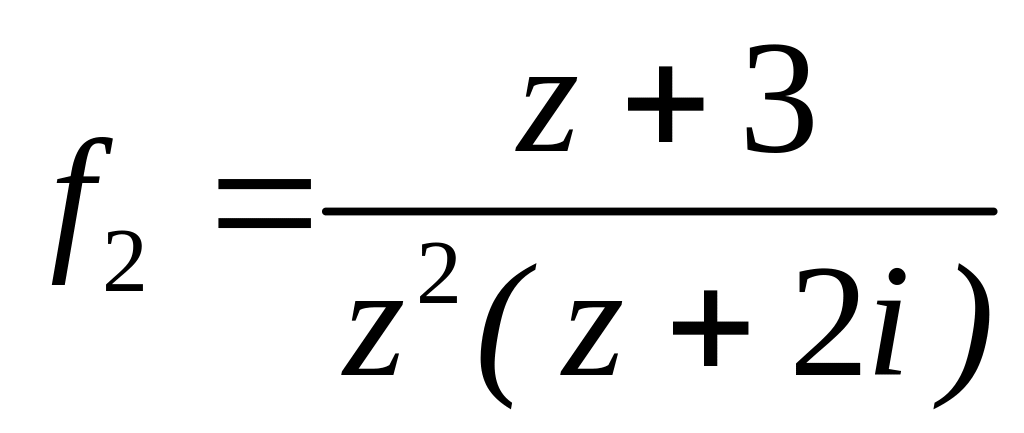 в околі точок
та
в околі точок
та

 за степенями
за степенями
 ;
; 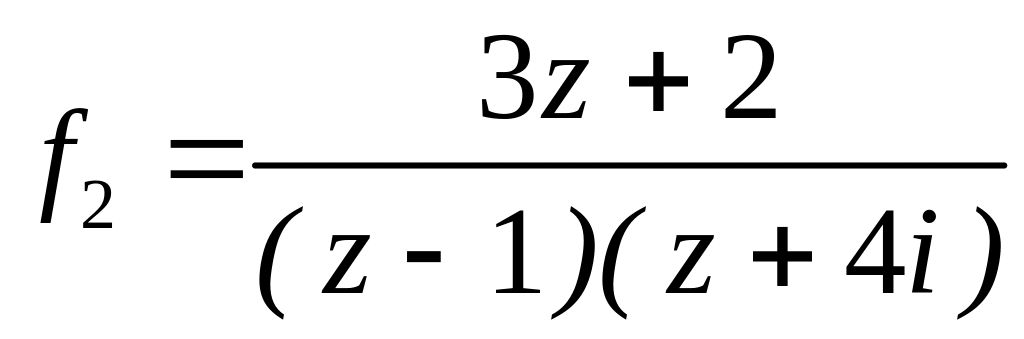 в околі точок
та
в околі точок
та
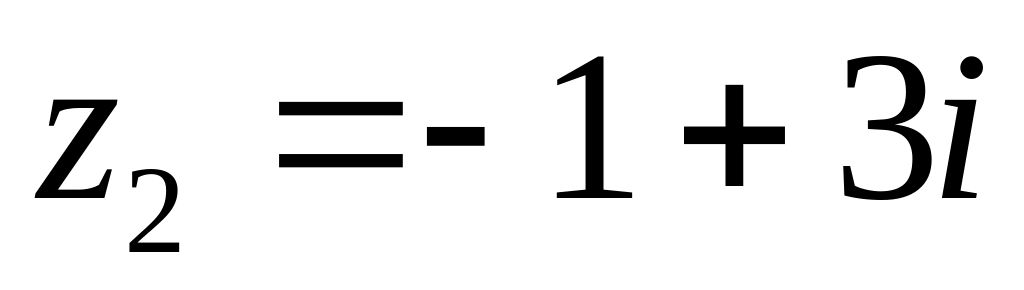
 за степенями
за степенями
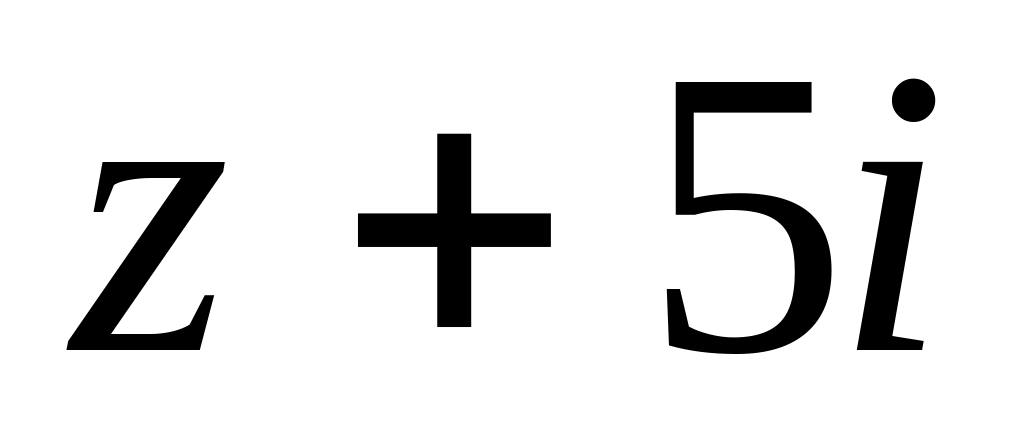 ;
;  в околі точок
та
.
в околі точок
та
.