Главные оси и моменты инерции.
Дифференцируя в (3: 1)Ju=Jxcos2a – Jxysin 2a + Jy sin2 a; 2) Jv=Jxsin2a + Jxysin 2a + Jy cos2 a; 3) Juv=Jxycos2a + sin 2a(Jx-Jy)/2 )
выражение Iu по и приравнивая его нулю, находим значение = 0 , при котором функция Iu принимает экстремальное значение:
. (5)
С учетом (3.(2)) можно утверждать, что при = 0 один из осевых моментов Iu или Iv будет наибольшим, а другой наименьшим. Одновременно при = 0 Iuv обращается в нуль, что легко установить из третьей формулы (3.(1)).
Декартовы оси координат, относительно которых осевые моменты инерции принимают экстремальные значения, называются главными осями инерции. Осевые моменты инерции относительно главных осей называются главными и определяются из (3) с учетом (5) и имеют вид:
. *IJ
Определение моментов инерции простейших фигур.
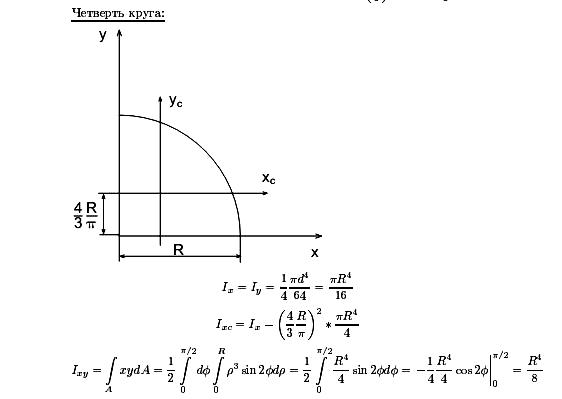
Для круга. Из (4) определим осевой момент инерции круга относительно диаметра. Т.к. в силу симметрии Jx=Jy, получаем Jx=Jy=Jp/2. Известно, что для круга Jp=πD4/32. => Jx=Jy=πD4/64.
Для толстостенного кольца: Jx=Jy= πD4[1-(d/D)4]/64
Для
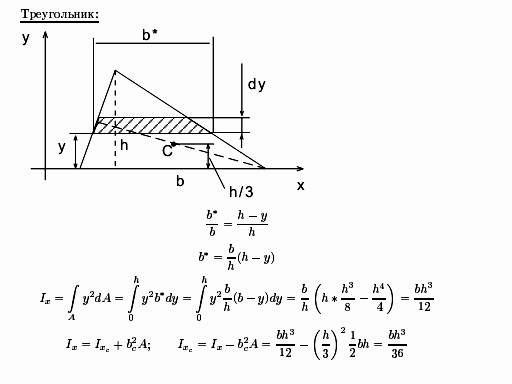
прямоугольного сечения: Jx=bh3/12;
Jy=hb3/12
; Jxy=0
Р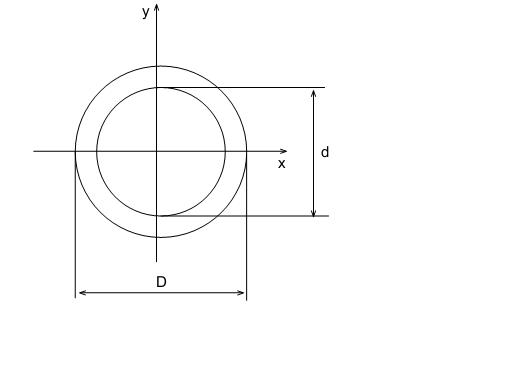
ациональные
формы поперечных сечений при кручении
и изгибе
В
этом расчете по заданной нагрузке (Nz)
определяются размеры поперечного
сечения стержня (F) из заданного материала
(
дано). Минимальное значение F получим,
если в условии прочности (1) принять знак
равенства:
Определение допускаемой нагрузки, то есть максимального значения нагрузки, которое допускает данный элемент конструкции (F и даны) при выполнении условия прочности.
