1)Напряженное состояние "чистый сдвиг": определение, условие парности касательных напряжений, напряжение в наклонных площадках

Чистым сдвигом называют такой вид напряженного состояния, при котором по граням выделенного из материала элемента действуют только касательные напряжения.

Напряжение в наклонных сечениях (площадках)

Рассмотрим более подробно особенности напряженного состоя­ния, возникающего в однородном растянутом стержне. Определим напряжения, возникающие на некоторой наклонной площадке, со­ставляющей угол  с плоскостью нормального сечения (рис. 2.6, а).

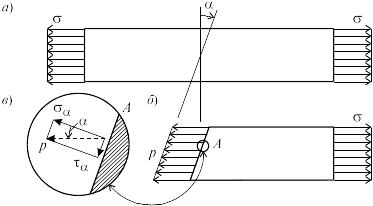
Рис. 2.6

Из условия z = 0, записанного для отсеченной части стержня (рис. 2.6, б), получим:

р F =  F, (2.17)

где F  площадь поперечного сечения стержня, F = F/cos   пло­щадь наклонного сечения. Из (2.17) легко установить:

р =  сos . (2.18)

Раскладывая напряжение р по нормали и касательной к на­клонной площадке (рис. 2.6, в), с учетом (2.18) получим:

 = p cos  =  cos2 ;      = p sin  =   sin 2  . (2.19)

П олученные выражения показывают, что для одной и той же точки тела величины напряжений, возникающих в сечениях, про­ходящих через эту точку, зависят от ориентации этой площадки, т.е. от угла . При  = 0 из (2.19) следует, что  = ,  = 0. При 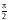 =  , т.е. на продольных площадках,  =  = 0. Это означает, что продольные слои растянутого стержня не взаимодействуют друг с другом. Касательные напряжения  принимают наибольшие зна­чения при  =  , и их величина составляет max= . Важно отме­тить, как это следует из (2.19), что . Следовательно, в любой точке тела на двух взаимно перпендикулярных площадках касательные напряже­ния равны между собой по абсолютной величине. Это условие является общей закономерностью любого напряженного состояния и носит название

закона парности касательных напряжений

Чистый сдвиг — напряженное состояние, при котором по взаимно перпендикулярным площадкам (граням) элемента возникают только касательные напряжения. Касательные напряжения 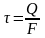, где Q — сила, действующая вдоль грани, F — площадь грани. Площадки, по которым действуют только касательные напряжения, называются площадками чистого сдвига. Касательные напряжения на них — наибольшие. Чистый сдвиг можно представить как одновременное сжатие и растяжение, происходящее по двум взаимно перпендикулярным направлениям. Т.е. это частный случай плоского напряженного состояния, при котором главные напряжения: ₁= — ₃ = ; ₂= 0. Главные площадки составляют с площадками чистого сдвига угол 45^о.

П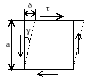 ри деформации элемента, ограниченного площадками чистого сдвига, квадрат превращается в ромб.  — абсолютный сдвиг,

  — относительный сдвиг или угол сдвига.

2)Чистый сдвиг. Главные напряжения. Закон Гука.

Чистый сдвиг

Ч истый сдвиг — напряженное состояние, при котором по взаимно перпендикулярным площадкам (граням) элемента возникают только касательные напряжения. Касательные напряжения , где Q — сила, действующая вдоль грани, F — площадь грани. Площадки, по которым действуют только касательные напряжения, называются площадками чистого сдвига. Касательные напряжения на них — наибольшие. Чистый сдвиг можно представить как одновременное сжатие и растяжение, происходящее по двум взаимно перпендикулярным направлениям. Т.е. это частный случай плоского напряженного состояния, при котором главные напряжения: ₁= — ₃ = ; ₂= 0. Главные площадки составляют с площадками чистого сдвига угол 45^о.

П ри деформации элемента, ограниченного площадками чистого сдвига, квадрат превращается в ромб.  — абсолютный сдвиг,

  — относительный сдвиг или угол сдвига

Закон Гука при сдвиге

:  = /G или  = G .

G — модуль сдвига или модуль упругости второго рода [МПа] — постоянная материала, характеризующая способность сопротивляться деформациям при сдвиге. (Е — модуль упругости, — коэффициент Пуассона).

Билет 22

1) Изменение моментов инерции плоской фигуры при повороте осей.