1. Кручение стержня прямоугольного поперечного сечения, напряжения и перемещения.

Кручение бруса прямоугольного сечения, напряжения в поперечном сечении

П ри этом нарушается закон плоских сечений, сечения некруглой формы при кручении искривляются – депланация поперечного сечения.

Эпюры касательных напряжений прямоугольного сечения.

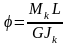; , Jk и Wk — условно называют моментом инерции и моментом сопротивления при кручении. Wk= hb2,

Jk= hb3, Максимальные касательные напряжения max будут посредине длинной стороны, напряжения по середине короткой стороны: = max, коэффициенты: ,, приводятся в справочниках в зависимости от отношения h/b (например, при h/b=2, =0,246; =0,229; =0,795.

При расчете бруса на кручение (вала) требуется решить две ос­новные задачи. Вопервых, необходимо определить напряжения, возникающие в брусе, и, вовторых, надо найти угловые перемеще­ния сечений бруса в зависимости от величин внешних моментов.

Решение для вала с круглым поперечным сечением (рис. 4.1 а).

Механизм деформирования бруса с круглым поперечным сечением можно представить в виде. Предполагая, что каждое поперечное сечение бруса в результате действия внешних моментов поворачивается в своей плоскости на некоторый угол как жесткое целое. Данное предположение, зало­женное в основу теории кручения, носит название гипотезы пло­ских сечений.

Рис. 4.1

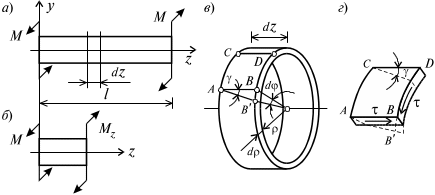
Для построения эпюры крутящих моментов Mz  применим тра­диционный метод сечений  на расстоянии z от начала координат рассечем брус на две части и правую отбросим (рис. 4.1, б). Для оставшейся части бруса, изображенной на рис. 4.1, б, составляя уравнение равенства нулю суммы крутящих моментов Mz  = 0, получим:

Mz = M. (4.1)

Поскольку сечение было выбрано произвольно, то можно сде­лать вывод, что уравнение (4.1) верно для любого сечения вала крутящий момент Mz  в данном случае постоянен по всей длине бруса.

Далее двумя поперечными сечениями, как это показано на рис. 4.1, а, из состава бруса выделим элемент длиной dz, а из него свою очередь двумя цилиндрическими поверхностями с радиусами  и  + d выделим элементарное кольцо, показанное на рис. 4.1, в. В результате кручения правое торцевое сечение кольца повернется на угол d. При этом образующая цилиндра АВ повернется на угол  и займет положение АВ . Дуга BВ  равна с одной стороны,  d, а с другой стороны   dz. Следовательно,

. (4.2)

Если разрезать образовавшуюся фигуру по образующей и раз­вернуть (рис. 4.1, г), то можно видеть, что угол  представляет со­бой не что иное, как угол сдвига данной цилиндрической поверх­ности под действием касательных напряжений , вызванных дейст­вием крутящего момента. Обозначая

, (4.3)

  относительный угол закручивания.

Этот угол представляет собой угол взаимного поворота двух сечений, отнесенный к рас­стоянию между ними. Величина  аналогична относительному уд­линению при простом растяжении или сжатии стержня.

Из совместного рассмотрения (4.2) и (4.3) и после некоторых преобразований, получим:

 =  . (4.4)

Подставляя выражение (4.4) в выражение закона Гука для сдвига (2.23), в данном случае выражение касательных напряжений принимает следующий вид:

 = G  , (4.5)

где   касательные напряжения в поперечном сечении бруса. Пар­ные им напряжения возникают в продольных плоскостях  в осе­вых сечениях. Величину крутящего момента M_z можно определить через  с помощью следующих рассуждений. Момент относительно оси z от дей­ствия касательных напряжений  на элементарной площадке dF равен (рис. 4.2):

dM =   dF.

Рис. 4.2

Проинтегрировав это выражение по площади поперечного сечения вала, получим:

. (4.6)

Из совместного рассмотрения (4.5) и (4.6) получим:

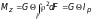. (4.7)

Откуда

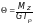. (4.8)

Величина G I_ называется жесткостью бруса при кручении.

Из (4.8), с учетом (4.3), интегрируя полученное выражение по параметру z, получим:

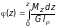. (4.9)

Если крутящий момент M_z и жесткость G I_ по длине бруса пос­тоянны, то из (4.9) получим:

, (4.10)

где  (0)  угол закручивания сечения в начале системы отсчета.

Для определения выражения напряжений, возвращаясь к формуле (4.5) и исключая из него , согласно (4.8), получим:

 ()= . (4.11)

Величина называется полярным моментом сопротивления поперечного сечения бруса в форме сплошного круга радиусом R. Определяется эта величина из следующих соображений:

(4.12)

Если же в брусе имеется внутренняя центральная полость ра­диусом r = 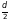 , то для кольца

, (4.13)

где с =  .