51. Применение производной второго порядка к исследованию функции на экстремум.
Выпуклость и вогнутость
свойство графика функции у = f (x) (кривой), заключающееся в том, что каждая дуга кривой лежит не выше (не ниже) своей хорды; в первом случае график функции f (x) обращён выпуклостью книзу (вогнутостью кверху) и сама функция называется выпуклой (рис. 1, а), во втором — график обращён вогнутостью книзу (выпуклостью кверху) и функция называется вогнутой (рис. 1, б). Если существуют производные f '(x) и f "(х), то первый случай имеет место при условии, что f "(x) ≥ 0, а второй при f "(x) ≤ 0 (во всех точках рассматриваемого промежутка). Выпуклость (книзу) можно охарактеризовать также тем, что дуга кривой лежит не ниже касательной, в окрестности любой своей точки (рис. 2, a), а вогнутость (книзу) — тем, что дуга кривой лежит не выше касательной (рис. 2, б). Аналогично определяются В. и в. поверхности.
Рис. 1 к ст. Выпуклость и вогнутость.
Определение. Кривая обращена выпуклостью вверх на интервале (а, b), если все ее точки лежат ниже любой ее касательной на этом интервале. Кривая, обращенная выпуклостью вверх, называется выпуклой, а кривая, обращенная выпуклостью вниз – называется вогнутой.
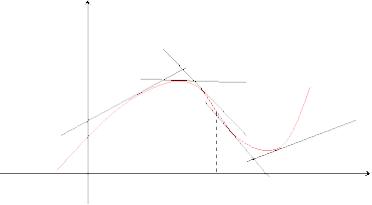
На рисунке показана иллюстрация приведенного выше определения.
Теорема 1. Если во всех точках интервала (a, b) вторая производная функции f(x) отрицательна, то кривая y = f(x) обращена выпуклостью вверх (выпукла).
Доказательство. Пусть х0 (a, b). Проведем касательную к кривой в этой точке.
Уравнение кривой: y = f(x);
Уравнение
касательной:
Следует
доказать, что
По
теореме Лагранжа для f(x)
– f(x0): 
, x0 < c < x.
По
теореме Лагранжа для
Пусть х > x0 тогда x0 < c1 < c < x. Т.к. x – x0 > 0 и c – x0 > 0, и кроме того по условию
,
следовательно, 
.
Пусть x < x0 тогда x < c < c1 < x0 и x – x0 <
0, c – x0 <
0, т.к. по условию 
то
.
Аналогично доказывается, что если f(x) > 0 на интервале (a, b), то кривая y=f(x) вогнута на интервале (a, b).
Теорема доказана.
Определение. Точка, отделяющая выпуклую часть кривой от вогнутой, называется точкой перегиба.
Очевидно, что в точке перегиба касательная пересекает кривую.
Теорема 2. Пусть кривая определяется уравнением y = f(x). Если вторая производная f(a) = 0 или f(a) не существует и при переходе через точку х = а f(x) меняет знак, то точка кривой с абсциссой х = а является точкой перегиба.
Доказательство. 1) Пусть f(x) < 0 при х < a и f(x) > 0 при x > a. Тогда при
x < a кривая выпукла, а при x > a кривая вогнута, т.е. точка х = а – точка перегиба.
1) Пусть f(x) > 0 при x < b и f(x) < 0 при x < b. Тогда при x < b кривая обращена выпуклостью вниз, а при x > b – выпуклостью вверх. Тогда x = b – точка перегиба.
Теорема доказана.
52. Необходимое условие выпуклости (вогнутости) графика функции
Необходимое условие перегиба.
Сформулируем необходимое условие перегиба графика функции.
Пусть
график функции y=f(x) имеет
перегиб в точке
и
имеет при 
непрерывную вторую производную, тогда
выполняется равенство 
.
Из
этого условия следует, что абсциссы
точек перегиба следует искать среди
тех, в которых вторая производная функции
обращается в ноль. НО, это условие не
является достаточным, то есть не все
значения
,
в которых вторая производная равна
нулю, являются абсциссами точек перегиба.
Еще
следует обратить внимание, что по
определению точки перегиба требуется
существование касательной прямой, можно
и вертикальной. Что это означает? А
означает это следующее: абсциссами
точек перегиба могут быть все
из области определения функции, для
которых 
и 
. Обычно это точки, в которых знаменатель
первой производной обращается в ноль.
ВОПРОС№53
Точки перегиба. Необходимое условие существования точки
перегиба.
Определение точки перегиба
Точка, в которой функция определена и в которой функция меняет направление выпуклости, называется точкой перегиба.
В окрестности такой точки x 0 график функции y = f (x) слева и справа от точки x0 имеет разные направления выпуклости.
Очевидно, что в точке перегиба касательная пересекает график функции так, что с одной стороны от этой точки график лежит под касательной, а с другой - над нею.
В окрестности точки перегиба график функции геометрически переходит с одной сторон касательной на другую и "перегибается" через нее. Отсюда и произошло название "точка перегиба".
Необходимое условие точки перегиба
Теорема. Пусть функция y = f (x) дважды непрерывно дифференцируема на интервале (a, b). Для того, чтобы точка М(x0, f(x0)) была точкой перегиба графика функции y = f (x) необходимо, чтобы f " (x0) = 0.
Доказательство. Предположим обратное, пусть f "(x0) ≠ 0. Тогда в силу непрерывности второй производной по теореме об устойчивости знака непрерывной функции существует окрестность точки x0, в которой f ″(x) < 0 (f "(x) > 0), и, значит график функции y = f (x) имеет определенное направление выпуклости в этой окрестности. Но это противоречит наличию перегиба в точке M(x0; f (x0 )). Полученное противоречие доказывает теорему.
Не всякая точка М (x0, f (x0)), для которой f " (x0) = 0, является точкой перегиба. Например, график функции y = f(x) = x4 не имеет перегиба в точке (0; 0), хотя f " (х) = 12·x ² = 0 при х = 0. Поэтому равенство нулю второй производной является лишь необходимым условием перегиба. Точки М (x0; f (x0)) графика, для которых f "(x0) = 0, будем называть критическими. Необходимо дополнительно исследовать вопрос о наличии перегиба в каждой критической точке, для чего следует сформулировать достаточное условие перегиба.
ВОПРОС №54
Достаточное условие точки перегиба
Теорема. Пусть функция y = f (x) имеет вторую производную f "(x) в некоторой достаточно малой окрестности точки x0 интервала (a, b), за исключением, быть может самой точки х0, а график функции имеет касательную в точке С = (х0, f (x0)). Если при переходе через точку х0 вторая производная f "(x) меняет знак, то точка С является точкой перегиба графика функции y = f (x).
Доказательство. Из того, что f "(x0) слева и справа от точки x0 имеет разные знаки, то направление выпуклости графика функции слева и справа от точки x0 является различным. Это и означает наличие перегиба в точке M(x0; f (x0)).