44) Теорема Лагранжа (о конечных приащениях).

Формула конечных приращений или теорема Лагра́нжа о среднем значении утверждает, что если функция непрерывна на отрезке и дифференцируема в интервале , то найдётся такая точка , что

.

Геометрически это можно переформулировать так: на отрезке найдётся точка, в которой касательная параллельна хорде, проходящей через точки графика, соответствующие концам отрезка.

Механическое истолкование: Пусть — расстояние точки в момент от начального положения. Тогда есть путь, пройденный с момента до момента , отношение — средняя скорость за этот промежуток. Значит, если скорость тела определена в любой момент времени , то в некоторый момент она будет равна своему среднему значению на этом участке.

Доказательство

Для функции одной переменной:

Введем функцию . Для нее выполнены условия теоремы Ролля: на концах отрезка ее значения равны . Воспользовавшись упомянутой теоремой, получим, что существует точка , в которой производная функции равна нулю:

что и требовалось доказать.

47. Формула Тейлора. Разложение элементарных функций по формуле Маклорена.

 формула

        

        

        изображающая функцию f (x), имеющую n-ю производную f ⁽ⁿ⁾(a) в точке х = а, в виде суммы многочлена степени n, расположенного по степеням х—а, и остаточного члена R_n (x), являющегося в окрестности точки а бесконечно малой более высокого порядка, чем (x—a) ⁿ [то есть R_n (x) = an (x)(x—a) ⁿ, где an (x) → 0 при х → а]. Если в интервале между а и х существует (n + 1)-я производная, то R_n (x) можно представить в видах:

        

        ,

        где ξ и ξ₁ — какие-то точки указанного интервала (остаточный член Т. ф. в формах Лагранжа и соответственно Коши). График многочлена, входящего в Т. ф.. имеет в точке а Соприкосновение не ниже n-го порядка с графиком функции f (x). Т. ф. применяют для исследования функций и для приближённых вычислений.

Разложение элементарных функций по формуле Маклорена.

48. Условия возрастания (убывания) функции на отрезке.

Определение возрастающей функции.Функция y=f(x) возрастает на интервале X, если для любых   и  выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.

Определение убывающей функции.Функция y=f(x) убывает на интервале X, если для любых   и  выполняется неравенство  . Другими словами – большему значению аргумента соответствует меньшее значение функции.

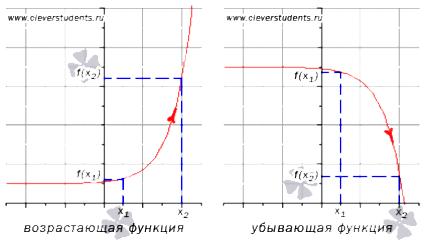
ЗАМЕЧАНИЕ: если функция определена и непрерывна в концах интервала возрастания или убывания (a;b), то есть при x=a и x=b, то эти точки включаются в промежуток возрастания или убывания. Это не противоречит определениям возрастающей и убывающей функции на промежутке X.

Достаточные условия возрастания и убывания функции.

На основании достаточных условий (признаков) возрастания и убывания функции находятся промежутки возрастания и убывания функции.

Вот формулировки признаков возрастания и убывания функции на интервале:

• если производная функции y=f(x) положительна для любого x из интервала X, то функция возрастает на X;

• если производная функции y=f(x) отрицательна для любого x из интервала X, то функция убывает на X.

Таким образом, чтобы определить промежутки возрастания и убывания функции необходимо:

• найти область определения функции;

• найти производную функции;

• решить неравенства    и   на области определения;

• к полученным промежуткам добавить граничные точки, в которых функция определена и непрерывна.