39. Инвариантность формы первого дифференциала.

Рассмотрим сложную функцию y=f(u(x)). Пусть функции y=f(u), u=u(x) дифференцируемы, тогда 

Таким образом, если аргументом функции является функция другого аргумента, то форма дифференциала совпадает с формой дифференциала, когда аргументом функции является независимая переменная. Это свойство называется инвариантностью формы дифференциала.

40. Производные высших порядков. Формула Лейбница.

Пусть y = f(x) является дифференцируемой функцией. Тогда производная также представляет собой функцию от x. Если она является дифференцируемой функцией, то мы можем найти вторую производную функции f, которая обозначается в виде

Аналогично, если f '' существует и дифференцируема, мы можем вычислить третью производную функции f:

Производные более высокого порядка (если они существуют), определяются как

Для нахождения производных высшего порядка можно использовать следующие формулы:

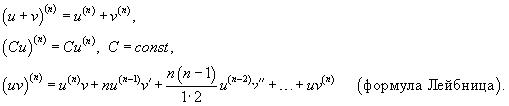
В частности, для производной второго и третьего порядка формула Лейбница принимает вид

41. Экстремумы функции. Необходимое условие существования экстремума.

Функция y=f ( x ) называется возрастающей ( убывающей ) в некотором интервале, если при x ₁ < x ₂ выполняется неравенство f (x ₁ ) < f (x ₂ ) ( f (x ₁ ) > f (x ₂)).

Если дифференцируемая функция y = f ( x ) на отрезке [ a , b ] возрастает (убывает), то ее производная на этом отрезке f ¢ ( x ) > 0 ( f ¢ ( x ) < 0).

Точка x _о называется точкой локального максимума ( минимума ) функции f ( x ), если существует окрестность точки x _о , для всех точек которой верно неравенство f ( x ) £ f ( x _о ) ( f ( x ) ³ f ( x _о )).

Точки максимума и минимума называются точками экстремума, а значения функции в этих точках - ее экстремумами.

Необходимые условия экстремума . Если точка x _о является точкой экстремума функции f ( x ), то либо f ¢ ( x _о ) = 0, либо f ¢ ( x _о ) не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек.

42. Достаточное условие экстремума.

Первое достаточное условие. Пусть x _о - критическая точка. Если f ¢ ( x ) при переходе через точку x _о меняет знак плюс на минус, то в точке x _о функция имеет максимум, в противном случае - минимум. Если при переходе через критическую точку производная не меняет знак, то в точке x _о экстремума нет.

Второе достаточное условие. Пусть функция f ( x ) имеет производную  f ¢ ( x ) в окрестности точки x _о и вторую производную    в самой точке x _о . Если f ¢ ( x _о ) = 0,   >0 (   <0), то точка x _о является точкой локального минимума (максимума) функции f ( x ). Если же   =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.

На отрезке [ a,b ] функция y = f ( x ) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [ a,b ].

43) Теорема 1. Ролля (о корнях производной).

Если функция f(х) непрерывна на промежутке [ а, b] , дифференцируема во всех его внутренних точках, а на концах принимает равные значения f(а)=f(b), то между а и b найдётся точка такая, что .

Доказательство

1. Пусть f(х) – тождественная константа на всём промежутке [а, b], но в этом случае её производная всюду равна нулю, то есть для любой точки .

2. Пусть . Тогда по теореме Вейерштрасса функция, непрерывная на промежутке [a, b], достигает на нём свои наибольшее и наименьшее значения, например, М > m. А так как f (a)=f (b), то М и m не могут одновременно быть значениями функции на концах промежутка и хотя бы одно из них достигается в некоторой точке , .

Пусть это будет М = f().

Придадим аргументу приращение . Тогда и функция получит соответствующее приращение для любого

Но по условию теоремы производная функции f (х) существует , а, значит, односторонние пределы в любой точке интервала должны совпадать между собой. В данном случае это возможно, если .

Теорема доказана и геометрически обозначает, что, если крайние ординаты кривой у=f (х) равны, то на кривой найдётся точка, где касательная параллельна оси ох (см. рис. 14).