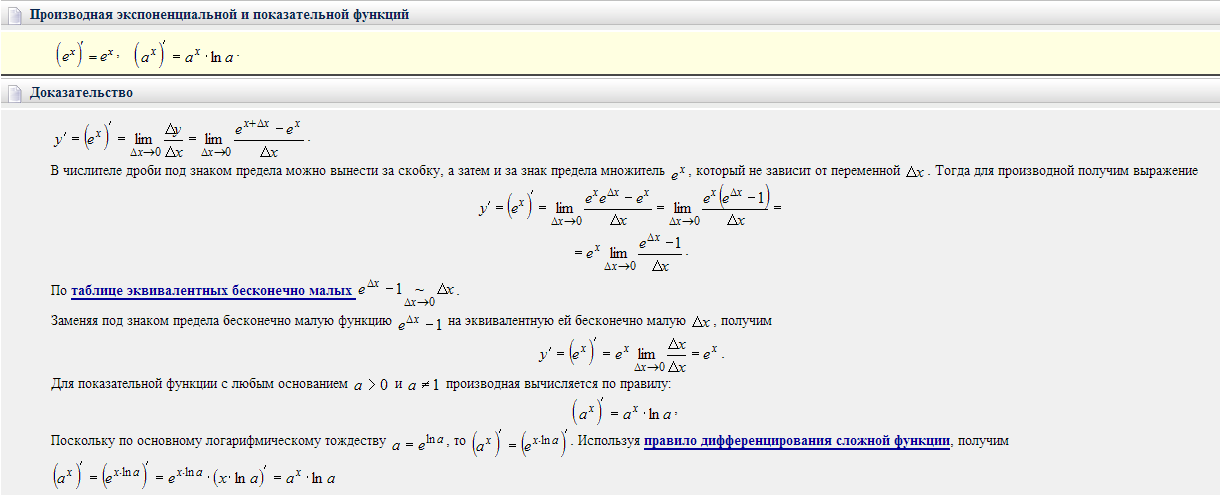
36. Вывод формул дифференцирования простейших элементарных

функций.

37. Вопрос. 2.

Уравнения касательной и нормали к плоской кривой К асательной к кривой l в ее точке М называют предельное положение секущей MN, когда точка N, двигаясь по кривой l, неограниченно приближается к точке М (рис. 25). Нормалью к кривой называется прямая, перпендикулярная касательной к этой кривой и проходящая через точку касания (рис. 26). ^ Геометрический смысл производной: – это угловой коэффициент касательной к графику в точке : Тогда из условия перпендикулярности прямых можно найти угловой коэффициент нормали: . Если существует, то уравнение касательной имеет вид: , (23) где . Если , то уравнение нормали имеет вид: .

38 Вопрос.

Дифференциал функции. Его геометрический смысл.

Дифференциалом функции называется линейная часть приращения функции относительно приращения аргумента

Δ f = A·Δx + o(Δx),

то есть df = A·Δx.

Связь дифференциала функции с её производной

Дифференциал функции равен произведению производной функции на приращение аргумента

dy = f '(x)·Δx.

В данном случае A = f ' (x). Действительно,

Дифференциал есть функция двух переменных, он зависит от аргумента x и приращения Δ x. Если считать, что y = x, то по определению дифференциала функции dx = 1·Δ x. Значит, dx = Δ x и dy = f ' (x)· Δ x.

Геометрический смысл дифференциала

Построим график функции y = f (x). В точке M(x, f (x)) проведем касательную MT. Как известно, tg α = f ' (x), из Δ ТМР имеем TP = MP· tg α, MP = Δ x = dx, поэтому

TP = f '(x)·dx = dy.

Дифференциал функции есть приращение ординаты касательной. Замечание. Из определения дифференциала следует, что производная функции равна отношению дифференциала функции к дифференциалу ее аргумента

Формула линеаризации функции

Определение дифференциала позволяет получить формулу для приближённого вычисления значений функции в некоторой окрестности S(x₀, δ) точки х₀. Полагая Δ f(x) ≈ df (x), получим формулу

f (x) ≈ f (x₀) + d f (x).

При х  х₀ погрешность вычисления по этой формуле есть бесконечно малая величина более высокого порядка, чем Δ х. Пример 1. Вычислить приближённо значение . Решение. В данном примере функция имеет вид где х = 8,24 и х₀ = 8. В этом случае , приращение аргумента Δ x = x - x₀ = 8,24 − 8 = 0,24, производная функции в точке х₀ = 8