20 Вопрос. Первый замечательный предел и его следствия

Первый замечательный предел имеет вид: 

На практике чаще встречаются модификации первого замечательного предела в виде

где, k – коэффициент.

Пояснение:

Следствия первого замечательного предела:

1. 

2. 

Эти следствия очень просто доказываются, если использовать правило Лопиталя или заменуэквивалентных бесконечно малых функций.

21 Вопрос - Второй замечательный предел и его следствия

Второй замечательный предел

 или 

Доказательство второго замечательного предела:

Доказательство для натуральных значений x 

  Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел для вещественных x, то есть докажем, что  . Рассмотрим два случая:

1. Пусть  . Каждое значение x заключено между двумя положительными целыми числами:  , где   — это целая часть x.

Отсюда следует:  , поэтому

.

Если  , то  . Поэтому, согласно пределу  , имеем:

.

По признаку (о пределе промежуточной функции) существования пределов  .

2. Пусть  . Сделаем подстановку  , тогда

.

Из двух этих случаев вытекает, что   для вещественного x.    

Следствия

1. 

2. 

3. 

4. 

5.  для  , 

6. 

22 Вопрос – Эквивалентность бесконечно малых функций Эквивалентные величины Определение

Если  , то бесконечно малые величины   и   называются эквивалентными ( ).

Очевидно, что эквивалентные величины являются частным случаем бесконечно малых величин одного порядка малости.

При   справедливы следующие соотношения эквивалентности (как следствия из так называемых замечательных пределов):

• 

• 

• 

• 

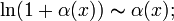
• , где  ;

• 

• , где  ;

• 

• 

• , поэтому используют выражение:

, где  .

Теорема

Предел частного (отношения) двух бесконечно малых величин не изменится, если одну из них (или обе) заменить эквивалентной величиной.

Данная теорема имеет прикладное значение при нахождении пределов

23. Теорема о связи функции, имеющей конечный предел и бесконечно

малой функцией

lim (x->a) f(x) = A (A +/- oo) <=> f(x)=A+alpha(x) - бесконечно малая при x->a

24. Непрерывность функции в точке

 Функция у = f (х) называется непрерывной в точке х₀, если в этой точке бесконечно малому приращению аргумента х-х₀= х соответствует бесконечно малое приращение функции

 у—у₀ = у, т. е. если

lim y = lim [ f (х₀ + х) – f (х₀)] = 0.

Этому определению равносильно следующее:

Функция f (х) называется непрерывной в точке х₀, если при х—> х₀ предел функции существует и равен ее частному значе­нию в этой точке, т. е. если lim f(х) = f (x₀).

 x->х₀

 

Для непрерывности функции f(х) в точке х₀ необходимо и достаточно выполнение следующих условий:

1)функция должна быть определена в некотором интервале, содержащем точку х_0.(т. е. в самой точке х₀ и вблизи этой точки);

2) функция должна иметь одинаковые односторонние пределы

 lim f (х) = lim f (x);

 x->х₀ -0  x->х₀ +0   

3) эти односторонние пределы должны быть равны f (x₀).

Функция f (x) называется разрывной в точке х₀, если она опре­делена в сколь угодно близких точках, но в самой точке х₀не удовлетворяет хотя бы одному из условий непрерывности.