
- •1. Перечень практических занятий.
- •1.1. Расчёт основных характеристик смесителя микроволнового приёмопередатчика.
- •1.1.1. Потери преобразования (коэффициент передачи):
- •1.1.2.Коэффициент шума
- •1.1.3. Компрессия
- •1.1.4. Интермодуляция
- •1.1.5. Изоляция по входному сигналу
- •1.1.6. Изоляция по цепи гетеродина
- •1.2. Расчёт соотношения сигнал-шум.
- •1.3. Расчёт максимальной скорости передачи информации при одно- и многоуровневом кодировании исходя из основных характеристик линии связи.
- •1.4. Расчёт предельных размеров зоны обслуживания (ячейки сотовой системы) и мощности базовой станции.
- •2. Контрольная работа
- •3. Курсовая работа Цели и содержание курсовой работы и её ориентировочная трудоёмкость.
- •3.1. Курсовая работа. Вариант 1.
- •3.1.1. Исследование микроволновой линии связи.
- •3.1.2. Описание лабораторного макета
- •3.1.3. Основные расчетные соотношения
- •3.1.4. Проведение измерений
- •3.1.5. Вычисления
- •3.1.6. Содержание пояснительной записки
- •3.2. Курсовая работа. Вариант 2.
- •3.2.1. Исследование диодного смесителя.
- •3.2.2. Общие сведения о смесителях свч
- •3.2.3. Описание объектов исследований и измерительной установки
- •3.2.4 Задания по лабораторной работе
- •3.2.5 Содержание пояснительной записки
- •Лабораторные работы.
- •1.1. Краткое описание измерителя микроволновых цепей.
- •1.2. Органы управления измерителем
- •1.3. Калибровка
- •1.3.1. Нормализация
- •1.3.2. Полная калибровка двухполюсника
- •1.3.3. Однопроходная калибровка четырехполюсника
- •1.3.4. Калибровка tosm
- •1.4. Проведение измерений.
- •1.4.1 Включение и выключение анализатора
- •1.4.2 Настройка прибора для измерения отраженного сигнала
- •1.4.3. Калибровка измерительного прибора
- •1.4.4. Анализ данных
- •1.4.5. Сохранение и печать данных
- •1. 5. Содержание отчёта.
- •6. Феер к. Беспроводная цифровая связь. Методы модуляции и расширения спектра: Пер. С англ. / Под ред. В. И. Журавлёва. – м.: Радио и связь, 2000.*
- •7. Телекоммуникационные системы и сети: учеб. Пособие для вузов: в 3 т. / Под ред. В.П.Шувалова. - 3-е изд., испр. И доп. - м. : Горячая линия-Телеком, 2003.*
1.3. Расчёт максимальной скорости передачи информации при одно- и многоуровневом кодировании исходя из основных характеристик линии связи.
Скорость
передачи информации по цифровому каналу
связи с шириной полосы пропускания
 и периодом выборки
и периодом выборки
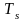 (длительностью одного бита) при
двухуровневом кодировании определяется
как
(длительностью одного бита) при
двухуровневом кодировании определяется
как
 .
Предполагается, что амплитудно-частотная
характеристика канала – прямоугольная.
Здесь
.
Предполагается, что амплитудно-частотная
характеристика канала – прямоугольная.
Здесь
 – частота выборки (частота следования
битов). Для увеличения скорости передачи
число амплитудных уровней может быть
увеличено (многоуровневое кодирование).
Тогда
– частота выборки (частота следования
битов). Для увеличения скорости передачи
число амплитудных уровней может быть
увеличено (многоуровневое кодирование).
Тогда
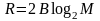 ,
где
,
где
 – число амплитудных уровней. Из последней
формулы следует, что, увеличивая
,
можно увеличивать скорость передачи
до бесконечности. На самом деле фактором,
ограничивающим скорость передачи,
являются шумы. Увеличения
можно добиться, уменьшая амплитудный
квант дискретного сигнала. Но предельным
значением кванта является амплитуда
шума. В соответствии с теоремой
Хартли-Шеннона ёмкость канала с белым
гауссовым шумом
– число амплитудных уровней. Из последней
формулы следует, что, увеличивая
,
можно увеличивать скорость передачи
до бесконечности. На самом деле фактором,
ограничивающим скорость передачи,
являются шумы. Увеличения
можно добиться, уменьшая амплитудный
квант дискретного сигнала. Но предельным
значением кванта является амплитуда
шума. В соответствии с теоремой
Хартли-Шеннона ёмкость канала с белым
гауссовым шумом
 бит/сек. Здесь
бит/сек. Здесь
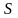 – мощность сигнала,
– мощность сигнала,
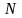 – мощность шума в полосе канала. Хотя
применимость этой теоремы ограничена
гауссовыми каналами (каналами с шумом,
подчиняющимся гауссову распределению),
она имеет большое значение, так как
многие каналы приблизительно гауссовы.
Теорема Хартли-Шеннона показывает, что
канал без шума имеет бесконечную емкость.
При наличии шума и увеличении полосы
ёмкость достигает некоторого верхнего
предела, при условии, что мощность
сигнала остается постоянной. Этот предел
можно определить, зная мощность шума в
полосе
– мощность шума в полосе канала. Хотя
применимость этой теоремы ограничена
гауссовыми каналами (каналами с шумом,
подчиняющимся гауссову распределению),
она имеет большое значение, так как
многие каналы приблизительно гауссовы.
Теорема Хартли-Шеннона показывает, что
канал без шума имеет бесконечную емкость.
При наличии шума и увеличении полосы
ёмкость достигает некоторого верхнего
предела, при условии, что мощность
сигнала остается постоянной. Этот предел
можно определить, зная мощность шума в
полосе
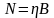 ,
где
,
где
 – спектральная плотность шума. Тогда
– спектральная плотность шума. Тогда
 .
.
Определить:
максимальные скорости передачи данных
в канале с шириной полосы пропускания
1 МГц с прямоугольной АЧХ в предположении
отсутствия шумов для двоичного
кодирования; то же для полосы пропускания
0,5 МГц,
 («белый шум» – спектральная плотность
мощности шума
(«белый шум» – спектральная плотность
мощности шума
 неизменна во всей рабочей полосе),
мощность сигнала 1 мВт.
неизменна во всей рабочей полосе),
мощность сигнала 1 мВт.
1.4. Расчёт предельных размеров зоны обслуживания (ячейки сотовой системы) и мощности базовой станции.
При
распространении в свободном пространстве
потери сигнала могут быть определены
по формуле
 ,
где
,
где
 – мощность сигнала
на входе приёмника,
– мощность сигнала
на входе приёмника,
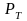 – мощность сигнала,
излучаемая передатчиком,
– мощность сигнала,
излучаемая передатчиком,
 и
и
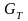 – коэффициенты усиления приёмной и
передающей антенн соответственно,
– коэффициенты усиления приёмной и
передающей антенн соответственно,
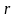 – расстояние между передающей и приёмной
антеннами. Коэффициенты усиления антенн
определяются соотношением
– расстояние между передающей и приёмной
антеннами. Коэффициенты усиления антенн
определяются соотношением
 ,
где
,
где
 – эффективная площадь антенны. При
распространении в реальных условиях
при наличии многолучёвости, затенений
и т. д. потери (в децибелах) составляют
– эффективная площадь антенны. При
распространении в реальных условиях
при наличии многолучёвости, затенений
и т. д. потери (в децибелах) составляют
 .
Коэффициент
.
Коэффициент
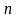 ,
учитывающий условия распространения
сигнала составляет 3,5÷5 для систем
мобильной связи вне зданий и 2÷4 для
связи внутри зданий.
,
учитывающий условия распространения
сигнала составляет 3,5÷5 для систем
мобильной связи вне зданий и 2÷4 для
связи внутри зданий.
Определить: потери при распространении сигнала в городских условиях принимая потери в свободном пространстве равными потерям по пути прямого прохождения на расстоянии L(d0)=50 дБ на частоте 890 МГц для GT=10 дБ, GR=0 дБ; определить радиус зоны обслуживания по полученным потерям при минимально допустимой мощности на входе приёмника 0,1 мкВт.
