4.5 Метод Рунге-Кутта
Этот метод основан на аппроксимации функции квадратной параболой. Он аналогичен методу Симпсона при численном вычислении определенного интеграла. Он является более точным, чем предыдущие два, но и существенно более трудоемким. Он требует на каждом шаге четырёх вычислений производных для каждого шага интегрирования. Увеличить его быстродействие можно за счет увеличения шага интегрирования.
Вычисления по данному методу выполняются в следующей последовательности.
По известным начальным условиям
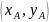определяем значение производной
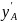в начальной точке:
.Из начальной точки
проводим прямую под углом наклона
и на середине шага получим точку
.
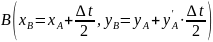Вычисляем значение производной
в точке
:
.Из начальной точки проводим прямую под углом наклона
и на середине шага получаем точку
.
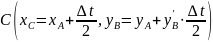Вычисляем значение производной
в точке
:
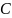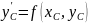.Из начальной точки проводим прямую под углом
и в конце шага интегрирования получим
точку
.
Находим значение производной
в точке
:
.Если аппроксимировать значение производных
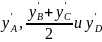квадратной параболой и взять интеграл,
то значение функции в конце шага
интегрирования определится по следующей
формуле:
.
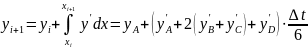Таблица 4.14 – Метод Рунге-Кутта
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
|
|
|
|
|
|
|
|
A |
10 |
585 |
2996 |
17707 |
0 |
8268,8 |
-111,243 |
-58,400 |
-52,843 |
B |
11 |
629,779 |
3302,532 |
17208,74 |
500 |
7734,3 |
-111,245 |
-64,176 |
-47,069 |
C |
11 |
634,376 |
3270,337 |
17140,113 |
500 |
7658,7 |
-111,206 |
-63,236 |
-47,970 |
D |
12 |
681,446 |
3567,340 |
16574,170 |
1000 |
7057,7 |
-111,332 |
-68,061 |
-43,271 |
|
12 |
572,130 |
3110,7 |
1981,4 |
|
|
|
44,505 |
|
|
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
|
|
|
|
|
|
|
|
|
A |
0,524 |
-0,852 |
306,532 |
-498,260 |
205 |
7926,79 |
295,069 |
9,752 |
1999,16 |
B |
0,436 |
-0,900 |
274,337 |
-566,887 |
201 |
8571,0488 |
295,069 |
9,754 |
1960,5138 |
C |
0,450 |
-0,893 |
285,670 |
-566,415 |
201 |
8571,0488 |
295,069 |
9,754 |
1960,5138 |
D |
0,374 |
-0,928 |
254,601 |
-632,097 |
197 |
9464,62 |
295,069 |
9,756 |
1921,8729 |
|
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
|
|
|
|
|
|
|
|
|
|
A |
1,983 |
15332,581 |
0,0247 |
0,0000 |
0,0153 |
0,0400 |
3,252 |
-10,175 |
0,1143 |
B |
2,134 |
19213,94 |
0,0234 |
0,0000 |
0,0146 |
0,0380 |
3,105 |
-7,906 |
0,0528 |
C |
2,150 |
19495,467 |
0,0233 |
0,0000 |
0,0146 |
0,0379 |
3,087 |
-7,844 |
0,0629 |
D |
2,309 |
24841,183 |
0,0218 |
0,0000 |
0,0138 |
0,0356 |
2,913 |
-5,960 |
0,0328 |
|
28 |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
36 |
|
|
|
|
|
|
|
|
|
|
A |
0,1543 |
2365,817 |
3,740 |
44,779 |
0,1553 |
-0,605 |
-9277,832 |
-5,524 |
-0,1008 |
B |
0,0908 |
1745,203 |
4,162 |
49,376 |
0,0819 |
-0,440 |
-8449,29 |
-5,011 |
-0,0844 |
C |
0,1008 |
1964,168 |
4,051 |
48,223 |
0,0964 |
-0,436 |
-8496,320 |
-5,030 |
-0,0843 |
D |
0,0684 |
1699,137 |
4,291 |
50,911 |
0,0600 |
-0,309 |
-7682,354 |
-4,538 |
-0,0703 |
Определение угла атаки при в т.С.
Таблица 4.15 – Определение угла атаки при в т.С.
99 |
100 |
101 |
102 |
103 |
104 |
105 |
106 |
107 |
108 |
№ |
|
|
|
|
|
|
|
|
|
1 |
0,513 |
3,600 |
0,000 |
-1,109 |
0,000 |
0,0000 |
0,038 |
737,903 |
4,724 |
2 |
|
|
|
|
-9,254 |
0,0850 |
0,123 |
2395,018 |
3,813 |
3 |
|
|
|
|
-7,369 |
0,0536 |
0,091 |
1782,860 |
4,149 |
4 |
|
|
|
|
-8,046 |
0,0629 |
0,101 |
1964,168 |
4,049 |
99 |
109 |
110 |
111 |
112 |
113 |
114 |
115 |
116 |
117 |
№ |
|
|
|
|
|
|
|
|
|
1 |
54,789 |
0,086 |
0,086 |
-0,096 |
-5,782 |
-33,313 |
0,0000 |
3,600 |
-9,254 |
2 |
45,897 |
0,072 |
0,072 |
-0,080 |
-4,770 |
-27,485 |
0,1300 |
3,730 |
-7,369 |
3 |
49,179 |
0,078 |
0,078 |
-0,086 |
-5,144 |
-29,636 |
0,0835 |
3,683 |
-8,046 |
4 |
48,198 |
0,076 |
0,076 |
-0,084 |
-5,032 |
-28,993 |
0,0964 |
3,696 |
-7,844 |
Определение угла атаки при в т.D.
Таблица
4.16 – Определение угла атаки при
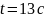в т.D.
99 |
100 |
101 |
102 |
103 |
104 |
105 |
106 |
107 |
108 |
№ |
|
|
|
|
|
|
|
|
|
1 |
0,403 |
3,316 |
0,000 |
-0,941 |
0,000 |
0,0000 |
0,036 |
884,346 |
4,743 |
2 |
|
|
|
|
-6,638 |
0,0410 |
0,077 |
1902,835 |
4,178 |
3 |
|
|
|
|
-5,703 |
0,0299 |
0,066 |
1627,097 |
4,331 |
4 |
|
|
|
|
-6,018 |
0,0328 |
0,068 |
1699,137 |
4,290 |
99 |
109 |
110 |
111 |
112 |
113 |
114 |
115 |
116 |
117 |
№ |
|
|
|
|
|
|
|
|
|
1 |
55,322 |
0,081 |
0,081 |
-0,076 |
-4,965 |
-22,007 |
0,0000 |
3,316 |
-6,638 |
2 |
49,811 |
0,073 |
0,073 |
-0,069 |
-4,433 |
-19,650 |
0,1300 |
3,446 |
-5,703 |
3 |
51,300 |
0,075 |
0,075 |
-0,071 |
-4,577 |
-20,287 |
0,0557 |
3,371 |
-6,018 |
4 |
50,906 |
0,075 |
0,075 |
-0,070 |
-4,539 |
-20,118 |
0,0600 |
3,376 |
-5,960 |
Применение метода Рунге-Кутта.
При
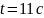в т.B
,
.
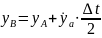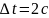Таким
образом,
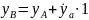то есть, получаем метод Эйлера.
При в т.С.
;
;
;
.
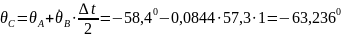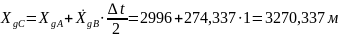При в т.D.
;
;
;
.
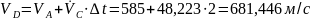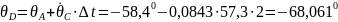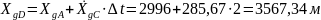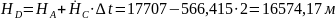При .
;
;
;
;
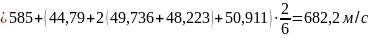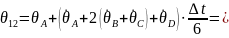
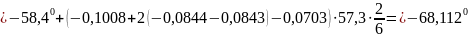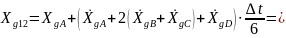
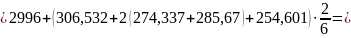
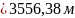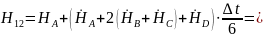
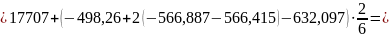
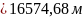Применив все три метода численного интегрирования, мы убедились, что наиболее точным является метод Рунге-Кутта. Хотя данный метод является наиболее трудоемким. Менее трудоемкими является модифицированный метод Эйлера. Наименее точным является метод Эйлера.