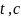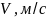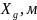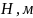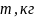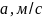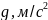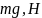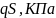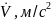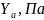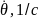4.2 Общие сведения о численном интегрировании обыкновенного дифференциального уравнения
Многие
задачи сводятся к решению одного или
нескольких обыкновенных дифференциальных
уравнений первого или более высокого
порядка. Причем дифференциальное
уравнение высокого порядка почти всегда
(если выделена старшая производная),
может быть сведено к системе дифференциальных
уравнений первого порядка. Решение
такой системы уравнений можно рассматривать
как решение одного уравнения
.
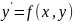Формальное отличие состоит в том, что вместо скалярных величин для системы уравнений необходимо вводить векторы. В нашем случае вектор y имеет следующую форму:
.
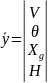Рассмотрим
простейшее обыкновенное дифференциальное
уравнение первого порядка
.
Необходимо найти
,
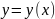т.е.решение этого уравнения.
Полученное
уравнение описывает множество решений.
Для выделения конкретного решения
необходимы дополнительные условия.
Задача значительно упрощается, если
начальные условия
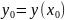задаются. Постановка задачи при данных
условиях есть задача Коши. При определенных
условиях решение этой задачи существует,
и оно является единственным.
В настоящее время разработано большое количество различных численных методов интегрирования обыкновенных дифференциальных уравнений первого прядка. При этом необходимо учитывать:
точность;
устойчивость вычислительной схемы;
трудоемкость;
необходимую память для хранения информации;
какая нужна информация перед каждым шагом (никакой, значения функций или производных в уже вычисленных точках).
При выполнении численного интегрирования в проекте используются три метода: метод Эйлера, модифицированный метод Эйлера и метод Рунге-Кутта.
4.3 Метод Эйлера
Сущность
метода Эйлера заключается в том что
производная
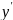на каждом шаге интегрирования принимается
постоянной, равной значению
в начале каждого шага. Таким образом
действительная интегральная кривая,
проходящая через заданную точку,
заменяется ломаной, состоящей из
прямолинейных отрезков (ломаная Эйлера):
,
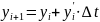где
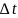- шаг интегрирования.
Метод
Эйлера обладает малой точностью и дает
сравнительно удовлетворительные
результаты лишь при очень малых шагах
интегрирования. Он является абсолютно
точным при
,
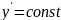т.е. для линейных зависимостей. Метод
является одношаговым, т.е. позволяет в
любой момент изменять шаг.
Таблица 4.3 – Метод Эйлера
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
|
|
|
|
|
|
|
18 |
832,000 |
4625,000 |
13239,000 |
3000 |
3623,8 |
-116,64 |
70,700 |
-187,343 |
19 |
629,779 |
3302,532 |
17208,74 |
500 |
7734,3 |
-111,245 |
-64,176 |
-47,069 |
12 |
679,155 |
3549,87 |
16641,85 |
1000 |
|
|
-69,012 |
|
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
|
|
|
|
|
|
|
|
0,331 |
0,944 |
274,988 |
785,242 |
163 |
15981,14 |
295,069 |
9,766 |
1591,8417 |
0,436 |
-0,900 |
274,337 |
-566,887 |
201 |
8571,0488 |
295,069 |
9,754 |
1960,5138 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
|
|
|
|
|
|
|
|
|
2,820 |
62526,01 |
0,0612 |
0,0000 |
0,0169 |
0,0781 |
0,139 |
0,830 |
0,0328 |
2,134 |
19213,94 |
0,0234 |
0,0000 |
0,0146 |
0,0380 |
3,105 |
-7,906 |
0,0528 |
28 |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
36 |
|
|
|
|
|
|
|
|
|
0,1109 |
6932,884 |
1,926 |
9,593 |
0,0600 |
0,003 |
179,706 |
0,204 |
-0,0015 |
0,0908 |
1745,203 |
4,162 |
49,376 |
0,0819 |
-0,440 |
-8449,29 |
-5,011 |
-0,0844 |
Определение угла
атаки
при
.
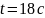Таблица 4.7 – Определение угла атаки при .
99 |
100 |
101 |
102 |
103 |
104 |
105 |
106 |
107 |
108 |
№ |
|
|
|
|
|
|
|
|
|
1 |
0,160 |
0,298 |
0,000 |
-0,129 |
0,000 |
0,0000 |
0,078 |
4882,031 |
3,215 |
2 |
|
|
|
-0,129 |
0,185 |
0,0002 |
0,078 |
4896,474 |
3,206 |
3 |
|
|
|
-0,129 |
0,190 |
0,0002 |
0,078 |
4896,881 |
3,206 |
99 |
109 |
110 |
111 |
112 |
113 |
114 |
115 |
116 |
117 |
№ |
|
|
|
|
|
|
|
|
|
1 |
22,182 |
0,027 |
0,027 |
-0,003 |
0,038 |
0,055 |
0,0000 |
0,298 |
0,185 |
2 |
22,093 |
0,027 |
0,027 |
-0,003 |
0,039 |
0,057 |
0,0005 |
0,299 |
0,190 |
3 |
22,090 |
0,027 |
0,027 |
-0,003 |
0,039 |
0,057 |
0,0005 |
0,299 |
0,190 |
Определение
угла атаки
при
.
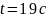Таблица 4.8 – Определение угла атаки при .
99 |
100 |
101 |
102 |
103 |
104 |
105 |
106 |
107 |
108 |
№ |
|
|
|
|
|
|
|
|
|
1 |
0,520 |
3,625 |
0,000 |
-1,075 |
0,000 |
0,0000 |
0,038 |
730,706 |
4,728 |
2 |
|
|
|
|
-9,053 |
0,0817 |
0,120 |
2301,254 |
3,863 |
3 |
|
|
|
|
-7,305 |
0,0528 |
0,091 |
1745,203 |
4,169 |
99 |
109 |
110 |
111 |
112 |
113 |
114 |
115 |
116 |
117 |
№ |
|
|
|
|
|
|
|
|
|
1 |
54,896 |
0,087 |
0,087 |
-0,094 |
-5,614 |
-32,823 |
0,0000 |
3,625 |
-9,053 |
2 |
46,462 |
0,074 |
0,074 |
-0,079 |
-4,685 |
-27,389 |
0,1238 |
3,749 |
-7,305 |
3 |
49,445 |
0,079 |
0,079 |
-0,084 |
-5,014 |
-29,310 |
0,0819 |
3,707 |
-7,906 |
Применение метода Эйлера при .
;
;
;
.
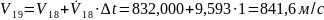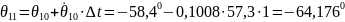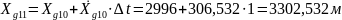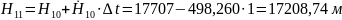Применение
метода Эйлера при
.
;
;
;
.
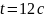
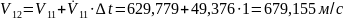
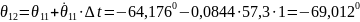
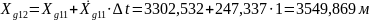
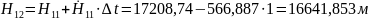