3. Определитель матрицы.

Пусть дана квадратная матрица: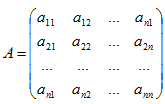 

Определителем, соответствующим данной квадратной матрице А, называют число, обозначаемое символом: 

Определителем второго порядка называют число 

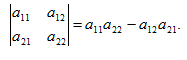
Пример 8: 

Определителем третьего порядка называют число 

Чтобы запомнить, какие произведения в правой части равенства (3) берутся со знаком "+”, а какие со знаком "-”, полезно использовать следующее правило треугольников (правило Саррюса): 

4. Вычисление определителей второго и третьего порядка.↑↑

5. Теорема разложения.

Рассмотрим квадратную матрицу  A  n-го порядка.        Выберем  i,j-ый элемент этой матрицы и вычеркнем  i-ую строку и  j-ый столбец. В результате мы получаем матрицу (n – 1)-го порядка, определитель которой называется минором элемента и обозначается символом  M_i j:

.

      Алгебраическое дополнение  A_i,j  элемента  a_i j определяется формулой

.

Теорема о разложении определителя по элементам строки. Определитель матрицы  A  равен сумме произведений элементов строки на их алгебраические дополнения:

Теорема о разложении определителя по элементам столбца. Определитель матрицы  A  равен сумме произведений элементов столбца на их алгебраические дополнения:

.

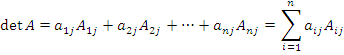      Теоремы о разложении определителя имеют важное значение в теоретических исследованиях. Они устанавливают, что проблема вычисления определителя n-го порядка сводится к проблеме вычисления n определителей (n –1)-го порядка. 

6. Свойства определителей.

Квадратной матрице    -го порядка ставиться в соответствие число , называемое определителем матрицы или детерминантом.

Свойства определителей:

Замечание

Все что будет сказано относительно строк, будет относиться и к столбцам.

1°    При транспонировании квадратной матрицы её определитель не меняется: 

Пример

Известно, что определитель матрицы   равен 3. Тогда определитель матрицы   , которая равна  , также равен 3.

2°    Общий множитель в строке можно выносить за знак определителя.

Пример

3°    

То есть, если квадратная матрица    -го порядка умножается на некоторое ненулевое число  , то определитель полученной матрицы равен произведению определителя исходной матрицы   на число   в степени, равной порядку матриц.

Пример

Задание. Пусть определитель матрицы   третьего порядка равен 3, вычислить определитель матрицы   .

Решение. По свойству 

Ответ. 

4°    Если каждый элемент в какой-то строке определителя равен сумме двух слагаемых, то исходный определитель равен сумме двух определителей, в которых вместо этой строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают с исходным определителем.

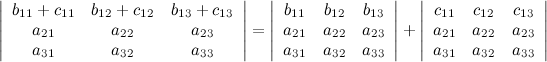
5°    Если две строки определителя поменять местами, то определитель поменяет знак.

Пример

6°    Определитель с двумя равными строками равен нулю.

Пример

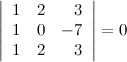
7°    Определитель с двумя пропорциональными строками равен нулю.

Пример

8°    Определитель, содержащий нулевую строку, равен нулю.

Пример

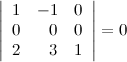
9°    Определитель не изменится, если к какой-то его строке прибавить другую строку, умноженную на некоторое число.

Пример

Пусть задан определитель третьего порядка 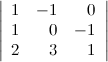  . Прибавим ко второй строке определителя третью его строку, при этом значение определителя не измениться:

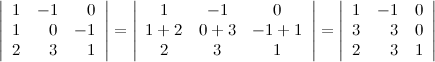
10°    Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов.

Пример

11°    Определитель произведения матриц равен произведению определителей: