18. Угловой коэффициент прямой.

Угловой коэффициент прямой — коэффициент   в уравнении   прямой на координатной плоскости, численно равен тангенсу угла (составляющего наименьший поворот от оси Ox к оси Оу) между положительным направлением оси абсцисс и данной прямой линией.^[1]

Тангенс угла может рассчитываться как отношение противолежащего катета к прилежащему. k всегда равен  , то есть производной уравнения прямой по x.

При положительных значениях углового коэффициента k и нулевом значении коэффициента сдвига b прямая будет лежать в первом и третьем квадрантах (в которых x и y одновременно положительны и отрицательны). При этом большим значениям углового коэффициента k будет соответствовать более крутая прямая, а меньшим — более пологая.

Прямые   и   перпендикулярны, если  , а параллельны при 

19. Уравнение прямой, проходящей через две заданные точки.

Прежде чем получить уравнение прямой, проходящей через две заданные точки в прямоугольной системе координат на плоскости, вспомним некоторые факты.

Одна из аксиом геометрии гласит, что через две несовпадающие точки на плоскости можно провести единственную прямую. Другими словами, задав две точки на плоскости, мы однозначно определяем прямую линию, которая через эти две точки проходит (при необходимости обращайтесь к разделу способы задания прямой на плоскости).

Пусть на плоскости зафиксирована прямоугольная декартова система координат Oxy. В этой системе координат любой прямой линии соответствует некоторое уравнение прямой на плоскости. С этой же прямой неразрывно связан направляющий вектор прямой. Этих знаний вполне достаточно, чтобы составить уравнение прямой, проходящей через две заданные точки.

Сформулируем условие задачи: составить уравнение прямой a, которая в прямоугольной декартовой системе координат Oxy проходит через две несовпадающие точки   и  .

Покажем самое простое и универсальное решение этой задачи.

Нам известно, что каноническое уравнение прямой на плоскости вида   задает в прямоугольной системе координат Oxy прямую линию, проходящую через точку   и имеющую направляющий вектор  .

Напишем каноническое уравнение прямой a, проходящей через две заданные точки  и  .

Очевидно, направляющим вектором прямой a, которая проходит через точки М1 и М2, является вектор  , он имеет координаты   (при необходимости смотрите статьювычисление координат вектора по координатам точек его конца и начала). Таким образом, мы имеем все необходимые данные, чтобы написать каноническое уравнение прямой a – координаты ее направляющего вектора   и координаты лежащей на ней точки   (и  ). Оно имеет вид   (или  ).

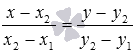20. Уравнение прямой, проходящей через заданную точку в заданном направлении.

Предположим, что прямая проходит через точку M₁ (x₁,y₁) и образует с осью OX угол . Составим уравнение этой прямой.

Будем искать уравнение прямой в виде уравнения с угловым коэффициентом: y = k · x + b. Угловой коэффициент прямой можно найти, зная угол наклона k = tg . Возьмем произвольную точку M (x, y), лежащую на этой прямой, и найдем уравнение, связывающее переменные x и y. Так как точки М и M₁ лежат на прямой, то их координаты удовлетворяют уравнению прямой:

y = k · x + b,

y₁ = k · x₁ + b.

Вычитая эти равенства, получим:

y - y₁ = k · (x - x₁) - уравнение прямой, проходящей через данную точку в данном направлении.