Приклади розв’язання задач

Приклад 1. Розклад N₂O₅ є реакцією першого порядку, константа швидкості якої дорівнює 0,002 хв^-1. Визначити, скільки процентів N₂O₅ розкладеться за 5 годин.

Розв’язок: Приймаємо початкову концентрацію N₂O₅ за 100% (С₀ = 100%), а кількість N₂O₅, розкладеного за 5 годин позначимо через С_х.

Константа швидкості реакції першого порядку

k = 2,3/t ∙ lg С₀/(С₀-С_х)

Підставляємо числові значення k, t і С₀ в це рівняння:

0,002 = 2,3/(5∙60) ∙ lg 100/(100 – С_х),

звідки С_х = 45,12%.

Приклад 2. Визначити порядок реакції 2СО = СО₂ + С при 583 К, якщо в даному випадку тиск за 30 хв. зменшився від 1,049 ∙ 10⁵ до 0,924 ∙ 10⁵ Па, а в другому за той самий проміжок часу – від 0,714 ∙ 10⁵ до 0,624 ∙ 10⁵ Па при постійному об’ємі.

Розв’язок: Константа швидкості реакції першого порядку дорівнює

- для першого випадку :

k₁= 1/τ ∙ ln С₀/С = 2,3/30 ∙ lg (1,049 ∙ 10⁵ / 0,924 ∙ 10⁵) = 0,00422 хв^-1,

• для другого випадку:

k₂ = 2,3/30 ∙ lg (0,714 ∙ 10⁵/ 0,624 ∙ 10⁵) = 0,00449 хв^-1.

Оскільки маємо майже однакові значення константи швидкості для першого і другого випадків, то можна вважати, що розглянута реакція є реакцією першого порядку.

Тема 11. Залежність швидкості хімічної реакції від температури

Гетерогенні процеси за умов нестаціонарної дифузії. Кінетика топохімічних реакцій.

Література: 1ст.405-414 4ст.384-393, 436-451.

Залежність константи швидкості реакції від температури визначається рівнянням Арреніуса:

ln k = A – ∆E/RT,

де ∆E – енергія активації реакції;

R – універсальна газова стала;

А – стала (передекспоненційний множник).

Енергія активації – це мінімальний (порівняно з середньою величиною) надлишок енергії частинок реагуючої речовини в момент їх участі в акті хімічного перетворення.

Енергію активації можна визначити за формулою

∆E = 2,3 R lg(k_Т2/ k_Т1) Т₁Т₂/(Т₂ – Т₁) = 2,3 R lg(k_Т2/ k_Т1)/(1/Т₁ – 1/Т₂),

де k_Т1 – константа швидкості реакції при температурі Т₁;

k_Т2 – константа швидкості реакції при температурі Т₂.

При підвищенні температури на 10 градусів швидкість реакції збільшується приблизно в 2 – 4 рази (правило Вант-Гоффа):

k_Т2/ k_Т1 = γ^(Т2-Т1)/10,

де γ – температурний коефіцієнт швидкості реакції.

При однаковій початковій концентрації реагуючих речовин добуток константи швидкості реакції на період напіврозпаду є сталою величиною для певної реакції при будь-якій температурі:

k_Т1∙τ_Т1 = k_Т2 ∙τ_Т2 = const,

де τ_Т1 – період напіврозпаду речовини при температурі Т₁; τ_Т2 – період напіврозпаду речовини при температурі Т₂.

Приклади розв’язання задач

Приклад 1. У скільки разів збільшиться швидкість реакції при підвищенні температури від 293 до 373 К, якщо температурний коефіцієнт швидкості реакції дорівнює 3?

Розв’язок: За правилом Вант-Гоффа швидкість реакції при температурі Т₂ дорівнює

V_T2 = V_T1 ∙ γ^(Т2-Т1)/10.

Швидкість реакції при 373 К:

V₃₇₃ = V₂₉₃ ∙ 3^(373-293)/10 = V₂₉₃ ∙ 3⁸ = V₂₉₃ ∙ 6561.

Отже, при підвищенні температури на 80 градусів швидкість реакції збільшується в 6561 раз.

Приклад 2. Для реакції розкладу 2НІ = Н₂ + І₂ константи швидкості при 575 і 700 К відповідно дорівнюють 1,22 ∙ 10^-6 і 1,16 ∙ 10^-3 л моль^-1хв^-1.

Визначити енергію активації, константу швидкості реакції при 625 К і температурний коефіцієнт швидкості реакції.

Розв’язок: Енергія активації дорівнює

∆E = 2,3 R lg(k_Т2/ k_Т1) Т₁Т₂/(Т₂ – Т₁) = 2,3 ∙ 8,3 ∙ 575 ∙ 700 ∙lg(1,16 ∙ 10^-3/1,22 ∙ 10^-6) /(700 – 575) = 183,06 КДж/моль.

Температурний коефіцієнт швидкості реакції:

lgγ = 10 lg(k_Т2/ k_Т1) / (Т₂ – Т₁) = 10 lg (1,16 ∙ 10^-3/1,22 ∙ 10^-6) / (700 – 575) = 0,2382

γ = 1,731.

Константа швидкості реакції при 625 К:

k_Т2 = k_Т1∙γ^(Т2-Т1)/10 = К₅₇₅ γ^(625-575)/10 = 1,22 ∙ 10^-6(1,731)⁵ = 1,896 ∙ 10^-5 л моль^-1хв^-1.

Приклад 3. При 283 К реакція між 1л 0,05 М розчину етилацетату і 1л 0,05 М розчину гідроксиду натрію за 16,8 хв. протікає на 50%. Визначити, за який час відбудеться омилення половини ефіру при 308 К, якщо всі інші умови не змінюються. Температурний коефіцієнт швидкості реакції дорівнює 2.

Розв’язок: Час, протягом якого відбувається омилення 50% етилацетату, обернено пропорційний константі швидкості реакції:

τ₁/τ₂ = k_Т2/ k_Т1.

З іншого боку, відношення констант швидкостей реакції при Т₂ і Т₁ можна визначити за рівнянням

k_Т2/ k_Т1 = γ^(Т2-Т1)/10.

Звідси

τ₁/τ₂ = γ^(Т2-Т1)/10,

або

lgτ₂ = lgτ₁ – (Т₂ – Т₁)/10 ∙ lgγ = lg16,8 – (308 – 283)/10 ∙ lg2 = 1,2253 – 2,5 lg2 =

= 1,2253 – 2,5 ∙ 0,0301 = 0,4728.

τ₂ = 2,97 хв.

З а д а ч і

1. Визначити теплоту q_р, роботу та зміну внутрішньої енергії при перетворенні 36 г води в пару при сталому тиску і температурі 373 К, коли відомо, що за цих умов молярна теплота випаровування води дорівнює 40,905 кДж/моль. Вважати пару ідеальним газом. Об’ємом рідини знехтувати. Відповідь: 81,81 кДж; 6,20 кДж; 75,61 кДж.

2. Визначити ∆H і роботу при плавленні 2,698 г алюмінію, коли відомо, що при тиску 1,01325 ∙ 10⁵ Па і температурі плавлення 933,1 К зміна мольного об’єму алюмінію дорівнює 0,51 ∙ 10^-3 л/моль. Теплота плавлення алюмінію дорівнює 10,76 кДж/моль. Відповідь: 1,08 кДж; 5,17 Дж.

3. Визначити теплоту, роботу і ∆U випаровування 92,14 кг етанолу, коли відомо, що при тиску 1,01325 ∙ 10⁵ Па і температурі кипіння теплота випаровування дорівнює 47,5 МДж/кмоль і питомий об’єм пари становить 0,607 м³/кг. Об’ємом рідини знехтувати. Молярну масу етанолу виразити в кг/кмоль. Відповідь: 95 МДж; 5,67 МДж; 89,33МДж.

4. 180 г водяної пари конденсується в рідину при температурі 373 К і тиску 1,01325 ∙ 10⁵ Па. Теплота випаровування води дорівнює 40,905 кДж/моль. Обчислити теплоту, роботу і зміну внутрішньої енергії, вважаючи пару ідеальним газом і нехтуючи об’ємом рідини. Відповідь: - 409,05 кДж; - 31,01 кДж; - 378,04 кДж.

5. Яка робота буде виконана 44 г СО₂ при підвищенні температури на 100 К і сталому тиску? Відповідь: 831,4 Дж.

6. Яка кількість теплоти виділиться при ізотермічному стисканні 0,1 м³ ідеального газу, взятого при 298 К і тиску 1,01325 ∙ 10⁵ Па, якщо об’єм його зменшиться в 10 разів? Відповідь: - 25,44 кДж.

7. Визначити середню питому теплоємність заліза в інтервалі температур від 290 до 373 К, знаючи, що для заліза залежність мольної теплоємності від температури визначається рівнянням: С_р = 14,11 + 29,73 ∙ 10^-3Т. Відповідь: 0,43 Дж/(г∙К).

8. Визначити ∆Н перетворення α-Fe в γ-Fe при 1200 К, якщо перетворення відбувається при 1183 К з поглинанням тепла ( ∆Н⁰ = 903 Дж/моль). При цій температурі С_р(α-Fe) = 41,29 Дж/(моль∙К), С_р(γ-Fe) = 34,23 Дж/(моль∙К). Прийняти, що в даному температурному інтервалі С_р не залежить від Т. Відповідь: 782,88 Дж/моль.

9. Розрахувати ∆Н випаровування води при 60⁰С при умові, що теплоємності пари і рідкої води в інтервалі від 40 до 60⁰С не залежать від температури і відповідно рівні35,57 Дж/(моль∙К) і 75,47 Дж/(моль∙К), а ∆Н випаровування при 40⁰С складає 44,1 кДж/моль. Відповідь: 43,3 кДж/моль.

10. Обчислити молярну середню теплоємність свинцю в інтервалі температур від 273 до 373 К, знаючи, що для свинцю залежність істинної молярної теплоємності від температури визначається рівнянням: С_р = 26,61 + 9,63 ∙ 10^-3Т. Відповідь: 26,72 Дж/(моль∙К) .

11. Молярна теплоємність оксиду кальцію визначається рівнянням: С_р = 4,186 + 20,26 ∙ 10^-3Т. Визначити кількість теплоти, яка потрібна для нагрівання 100 г оксиду кальцію від 290 до 890 К. Відповідь: 17,3кДж.

12. Визначити стандартну ∆Н⁰ утворення карбонату кальцію з простих речовин, користуючись такими даними:

Са + 1/2О₂ = СаО, ∆Н⁰₁ = - 635,1 кДж;

С + О₂ = СО₂, ∆Н⁰₂ = - 393,78 кДж;

СаО + СО₂ = СаСО₃, ∆Н⁰₃ = - 178,62 кДж.

Відповідь: - 1207, кДж.

13. Визначити Q_p i Q_V при 298 К для реакції FeO_(тв.) + H_2(г) = Fe_(тв.) + H₂O_(рід.). Стандартні теплоти утворення (Q_p) FeO_(тв.) і H₂O_(рід.) відповідно дорівнюють 266,7 і 286,0 кДж/моль. Відповідь: 19,33 кДж; 16,86 кДж.

14. Визначити теплоту утворення води з водню і кисню (Q_V) при V = const і Т = 298 К, якщо теплота утворення води при р = const і Т = 298К дорівнює 286,03 кДж/моль. Відповідь: 282,32 кДж/моль.

15. Визначити ∆Н утворення оксиду цинку при 500 К і р = const, якщо ∆Н⁰_298(ZnO) = -348,3 кДж/моль, а температурні залежності теплоємностей даються рівняннями:

C_p^Zn = 22,4 + 10,05 ∙ 10^-3T;

C_p^O2 = 34,62 + 1,08 ∙ 10^-3T;

C_p^ZnO = 49,03 + 5,11 ∙ 10^-3T.

Відповідь: 1,09 кДж/моль.

16. При 2023 К ∆Н випаровування свинцю дорівнює 177,9 Дж/моль. Визначити ∆Н випаровування свинцю при 2500 К, якщо мольні теплоємності рідкого і газоподібного свинцю можна розрахувати за рівняннями:

С_р^рід. = 32,45 – 3,06 ∙ 10^-3T;

С_р^г. = 20,81.

Відповідь: - 175,65 Дж/моль.

17. Газ, розширюючись при постійному тиску 1 атм. Від 10 до 16 л, поглинає1254 Дж тепла. Визначити зміну внутрішньої енергії. (1 л∙атм/моль = 101,33 Дж/моль). Відповідь: 646 Дж.

18. Яка кількість тепла необхідна для нагрівання 1 м³ повітря від 0 до 1⁰С при постійному об’ємі і початковому тиску 1 атм? Густина повітря при нормальних умовах дорівнює 0,00129г/мл; С_р = 1 Дж/(г∙К); С_р/С_V = 1,4. Відповідь: 921 Дж.

19. Питома теплоємність алюмінію виражається рівнянням: С_р = 0,183 + 1,096 ∙ 10^-4T. Алюміній плавиться при 658,5⁰С, його питома теплота плавлення дорівнює 386,2 Дж/г. Обчислити, скільки тепла знадобиться на розплавлення 500 г алюмінію, якщо початкова температура була 25⁰С. Відповідь: 524,6 кДж.

20. Знайти ∆Н утворення аміаку на основі наступних даних:

2Н₂ + О₂ = 2Н₂О, ∆Н = -571,13 кДж;

4NH₃ + 3O₂ = 6H₂O + 2N₂, ∆Н = -1528,80 кДж.

Відповідь: - 46,15 кДж/моль.

21. Теплота розчинення BaCl₂ (Q_BaCl2) у воді дорівнює 8,653 кДж; теплота гідратації BaCl₂ (Q_h) з утворенням BaCl₂∙2Н₂О дорівнює 29,135 кДж. Чому дорівнює теплота розчинення BaCl₂∙2Н₂О? Відповідь: - 20,482 кДж.

22. Знайти теплоту розкладу Н₂О₂ (Q_Н2О2) на основі наступних даних:

SnCl₂ + 2HCl + 1/2O₂ = SnCl₄ + H₂O + 296,3 кДж;

SnCl₂ + 2HCl + H₂O₂ = SnCl₄ + 2H₂O + 393,0 кДж.

Відповідь: 96,7 кДж.

23. Знайти тепловий ефект (Q_х.р.) реакції CuS + O₂ = Cu + SO₂ при 727⁰С і тиску 1 атм. На основі наступних даних: Q утворення CuS і SO₂ при 25⁰С і 1 атм. Відповідно рівні 48,488 і 296,613 кДж/моль. Молярні теплоємності речовин задаються рівняннями:

С_р(CuS) = 10,6 + 2,64 ∙ 10^-3T;

С_р(О₂) = 6,502 + 1,738 ∙ 10^-3T;

С_р(Cu) = 5,43 + 1,41 ∙ 10^-3T;

С_р(SO₂) = 11,40 + 1,714 ∙ 10^-3T.

Відповідь: 251,31 кДж.

24. Молярна теплота випаровування бензолу (λ₁) при 0⁰С дорівнює 32,65 кДж/моль. Середня питома теплоємність парів бензолу в межах від 0 до 80⁰С дорівнює 1,25 Дж/(г∙К). Середня питома теплоємність рідкого бензолу в тому ж температурному інтервалі дорівнює 1,72 Дж/(г∙К). Визначити молярну теплоту випаровування бензолу (λ₂) при 80⁰С. Відповідь: 29,72 кДж/моль.

25. Вважаючи С_р кисню рівним 7/2 R і постійним, обчислити зміну ентропії при нагріванні 3,2 г кисню від 0 до 100⁰С: а) при постійному тиску; б) при постійному об’ємі. Відповідь: 0,908; 0,649 (Дж/град.).

26. Визначити зміну ентропії при нагріванні 1 моль срібла від 25 до 225⁰С. Молярна теплоємність срібла виражається рівнянням: С_р = 5,593 + 1,49 ∙ 10^-3Т. Відповідь: 3,17 Дж/(моль ∙ К).

27. Визначити зміну ентропії при плавленні 1 кг міді. Питома теплота плавлення міді дорівнює 173,9 Дж/г, температура плавлення міді 1083⁰С. Відповідь: 128,2 Дж/град.

27. Визначити стандартну зміну ізобарно-ізотермічного потенціалу для реакції ZnS + H₂ = Zn + H₂S за такими даними ∆Н⁰_ZnS = - 201,8 кДж/моль; ∆Н⁰_H2S = - 20,1 кДж/моль; S⁰_ZnS = 57,78 Дж/(моль ∙ К); S⁰_H2 = 306,74 Дж/(моль ∙ К); S⁰_Zn = 41,66 Дж/(моль ∙ К); S⁰_H2S = 205,57 Дж/(моль ∙ К). Чи може протікати ця реакція за стандартних умов? Відповідь: 216,65 кДж.

27. Обчислити зміну ентропії при нагріванні 11,87 г олова від 298 до 498 К. Залежність молярної теплоємності олова від температури визначається рівнянням С_р = 18,51 + 26,387∙10^-3Т. Відповідь: 1,478 Дж/град.

27. При 626 К α-Ni переходить в β-Ni. Обчислити зміну ентропії 5,871 г нікелю при нагріванні його від 298 К до температури фазового переходу, якщо залежність С_р від температури дається рівнянням: С_р = 17 + 29,48∙10^-3Т. Відповідь: 2,227 Дж/град.

27. Визначити зміну ентропії при переході 5,871 г β-Ni від 626 К в рідкий стан, якщо теплота плавлення β-Ni при 1728 К дорівнює 17,63 кДж/моль, а теплоємність β-Ni визначається рівнянням: С_р = 25,2 + 7,536∙10^-3Т. Відповідь: 4,41 Дж/град.

27. Визначити зміну ентропії при нагріванні 1 м³ СО₂ від 298 до 1000 К при тиску 1,01325 ∙ 10⁵ Па. Залежність молярної теплоємності СО₂ від температури виражається рівнянням: С_р = 32,24 + 22,2 ∙ 10^-3Т. Відповідь: 2,44 кДж/град.

27. Ентропія α-заліза за стандартних умов дорівнює 27,177 Дж/(моль ∙ К). Залежність теплоємності α-заліза від температури дається рівнянням: С_р = 14,11 + 29,73 ∙ 10^-3Т. При 1033 К α-залізо перетворюється в β-залізо. Визначити ентропію α-заліза при температурі фазового переходу. Відповідь: 66,57 Дж/(моль ∙ К).

27. Обчислити ∆U і ∆F для реакції Ag + 1/2Cl₂ = AgCl при 298 К і 1 атм., якщо ∆Н_{реакції} = -127,068 кДж/моль і ∆G_{реакції} = -109,748 кДж/моль. Відповідь: -125,829; -108,509 кДж/моль.

27. Розрахувати ∆G при 400 К для реакції 0,5N₂ + 1,5H₂ = NH₃, якщо ∆G при 298 К дорівнює –16,496 кДж/моль; S⁰_NH3 = 192,5; S⁰_N2 = 191,5; S⁰_H2 = 130,6 Дж/моль^.К. Відповідь: - 6,383 кДж/моль.

27. Розрахувати зміну ентропії при нагріванні 58,82 г В₂О₃ від 298 до 700 К, теплоємність В₂О₃ С_Р = 36,5525 + 106,345^.10^-3Т (Дж/(моль^.К)). Відповідь: 62,5 Дж/(моль^.К).

27. Бромбензол кипить при 429,8 К, його теплота пароутворення при цій температурі 241,9 Дж/г. Розрахувати зміну ентропії при випаровуванні 1 молю бромбензолу. Відповідь: 88,4 Дж/(моль^.К).

27. Чи буде взаємодіяти водень з киснем за реакцією 2Н₂+ О₂ = 2Н₂О при 180 К і 1,013^.10⁵ Па, якщо ∆G⁰_{298 Н2О} = -237,19 кДж/моль; S⁰_H2 = 130,6; S⁰_О2 = 205,03; S⁰_H2О = 69,94 Дж/(моль^.К). Відповідь: ∆G⁰_{180 Н2О} = -275,7 кДж, буде.

27. Чи буде взаємодіяти азот з воднем за реакцією 3Н₂ + N₂ = 2NH₃ при 700 К і тиску 1 атм., якщо ∆G⁰_{298 NH3} = - 17,0 кДж/моль; S⁰_H2 = 130,6; S⁰_N2 = 191,5; S⁰_NH3 = 192,5 Дж/(моль^.К). Відповідь: ∆G⁰_{700 NH3} = 62,7 кДж, не буде.

27. Обчислити зміну ізобарного потенціалу при ізотермічному стисканні 10^-2 м³ кисню. Початковий і кінцевий тиск відповідно дорівнюють 1,01325^.10⁵ Па і 1,01325 МПа, температура 273 К. Відповідь: 2,33 кДж.

27. В якому напрямку буде протікати реакція ZnS + H₂ = Zn + H₂S за стандартних умов, якщо: ∆Н⁰_{298 ZnS} = - 201,8; ∆Н⁰_{298 H2S} = - 20,1 кДж/моль; S⁰_{298 ZnS} = 57,78; S⁰_{298 H2} = 306,74; S⁰_{298 Zn} = 41,66; S⁰_{298 H2S} = 205,57 Дж/(моль^.К). Відповідь: ∆G⁰_х.р. = 216,75 кДж, в зворотному напрямку.

27. Обчислити зміну ізобарного потенціалу при ізотермічному стисненні 160 г кисню від 0,101325^.10⁶ до 1,01325^.10⁶ Па, якщо температура газу становить 300 К. Відповідь: 28,635 кДж.

27. Визначити ізобарний потенціал утворення СО₂ при 298 і тиску 1,01325^.10⁵ Па , якщо в стандартних умовах він дорівнює 394,8 кДж/моль. Відповідь: - 360,63 кДж.

27. В якому напрямку піде реакція ZnO + CO = Zn + CO₂ при 298 К, якщо теплоти утворення ZnO, CO і CO₂ відповідно дорівнюють 348,3; 110,6 і 393,78 кДж/моль, а ентропії ZnO, CO, Zn і CO₂ - відповідно 43,5; 198,04; 41,66 і 213,78 Дж/(моль^.К). Відповідь: ∆G⁰_х.р. = 60,978 кДж/моль, реакція піде в зворотному напрямку.

27. Побудувати графічну залежність ∆G від температури для реакції С₆Н_6(р) + 7/2 О_2(г) = 6 СО_2(г) + 3 Н₂О_(г) , ∆Н = -3037,5 кДж. Як впливає зміна температури на протікання прямої і зворотної реакції?

27. Побудувати графічну залежність ∆G від температури для реакції СН₃ОН_(р) + 3/2 О_2(г) = СО_2(г) + 2Н₂О_(р), ∆Н = -726,6 кДж. Як впливає зміна температури на протікання прямої і зворотної реакції?

27. При яких температурах буде протікати пряма, а при яких - зворотна реакція СО_(г) + 2Н_2(г) ↔ СН₃ОН_(г), ∆Н = -128,05 кДж, якщо ентропії учасників реакції відповідно рівні: 197,91; 130,59 і 126,8 Дж/(моль^.К). Відповідь: при Т < 385 К – пряма.

27. При яких температурах буде протікати пряма, а при яких - зворотна реакція СН_4(г) + СО_2(г) ↔ 2СО_(г) + 2Н_2(г), ∆Н = 247,37 кДж, якщо ентропії учасників реакції відповідно рівні: 186,19; 213,65; 197,91 і 130,59 Дж/(моль^.К). Відповідь: при Т > 962 К – пряма.

27. Тиск пари метанолу при 20⁰С дорівнює 94 мм.рт.ст., а при 40⁰С – 259,4 мм.рт.ст. Визначити середнє значення теплоти випаровування спирту у вказаному інтервалі температур. Відповідь: 38,7 кДж/моль.

50. Молярна теплота випаровування CCl₄ змінюється з температурою за рівнянням: λ = 10960 – 10,53Т. Визначити тиск насиченої пари CCl₄ при 60⁰С, якщо відомо, що CCl₄ кипить при 75⁰С під тиском 760 мм.рт.ст. Відповідь: 677 мм.рт.ст.

51. Константа рівноваги К_р реакції С + СО₂ ↔ 2СО при 1000 К дорівнює 1,862. Знайти константу рівноваги при 1200 К, якщо середнє значення теплового ефекту Q_p дорівнює –169,4 кДж. Відповідь: 55,56.

52. При 676 К константа рівноваги (К_р) реакції MgCO₃ ↔ MgO + CO₂ дорівнює 1. ∆Н = 117,49 кДж. Знайти К_р при 700 К, вважаючи, що ∆Н в цьому інтервалі температур не змінюється. Відповідь: 2,05.

53. Пружність пари аміаку над HgCl∙NH₃ дорівнює 35,2 мм.рт.ст. при 167⁰С і 66,2 мм.рт.ст при 185⁰С. Визначити середнє значення теплового ефекту (∆Н) реакції HgCl∙NH₃ ↔ HgCl + NH₃. Відповідь: 58,8 кДж.

54. Константа рівноваги реакції 2СО₂ ↔ 2СО + О₂ К_р = 10^-20 при 1000 К. Обчислити константу рівноваги цієї реакції при 2000 К, якщо середнє значення теплового ефекту Q_p дорівнює - 560,8 кДж. Відповідь: 4,44 ∙ 10^-6

55. При якій температурі константа рівноваги реакції СО + Н₂О ↔ СО₂ + Н₂ дорівнює 27,56, якщо при 1080 К К_р = 1? Тепловий ефект реакції (Q_p) вважати рівним 41,16 кДж. Відповідь: 626,6 К.

56. Пружність дисоціації СаСО₃ при 1150 К дорівнює 0,66 атм. Теплота дисоціації (Q_p) дорівнює -167,2 кДж. Визначити температуру, при якій пружність дисоціації карбонату кальцію, що протікає за рівнянням СаСО₃ → СаО + СО₂, дорівнює 1 атм. Відповідь: 1176 К.

57. Константа рівноваги реакції 2А + В = 2С + D, де всі учасники – гази, дорівнює 2. В який бік піде реакція в суміші, що складається з 20 мол.% А, 30 мол.% В, 30 мол.% С і 20 мол.% D? Відповідь: праворуч.

58. Константа рівноваги реакції А + В = С + D, де всі учасники – гази, дорівнює 4. В який бік піде реакція в суміші, що складається з 10 мол.% А, 20 мол.% В, 30 мол.% С і 40 мол.% D? Відповідь: ліворуч.

59. Константа рівноваги реакції А + В = С + D, де всі учасники – гази, дорівнює 6. В який бік піде реакція в суміші, що складається з 10 мол.% А, 20 мол.% В, 30 мол.% С і 40 мол.% D? Відповідь: стан рівноваги.

60. Константа рівноваги реакції 2А + В = 2С + D, де всі учасники – гази, дорівнює 1,5. В який бік піде реакція в суміші, що складається з 20 мол.% А, 30 мол.% В, 30 мол.% С і 20 мол.% D? Відповідь: стан рівноваги.

61. Визначити зміну вільної енергії Гіббса при перетворенні 1 моль СО при тиску 2 атм. і 1 моль Cl₂ при тиску 3 атм. в 1 моль СОCl₂ при тиску 0,5 атм., якщо Т = 600⁰С і К_р для реакції СО + Cl₂ ↔ СОCl₂ дорівнює 0,766. Відповідь: - 16,1 кДж.

62. Визначити константу рівноваги (К_р) для реакції 2С + 3Н₂ ↔ С₂Н₆ при 298 К, якщо: S^o_298(C2H6) = 229,3; S^o_298(C) = 5,7; S^o_298(H2) = 130,5 Дж/(моль К) і ∆Н^о_298(С2Н6) = -84586,5 Дж/моль. Відповідь: 5,74 ∙ 10⁵.

63. Визначити константу рівноваги (К_р) для реакції 6С + 3Н₂ ↔ С₆Н₆ при 298 К, якщо: S^o_298(C6H6) = 269,4; S^o_298(C) = 5,7; S^o_298(H2) = 130,5 Дж/(моль К) і ∆Н^о_298(С6Н6) = 82,848 кДж/моль. Відповідь: 2,06 ∙ 10^-23.

64. Визначити константу рівноваги (К_р) реакції Н₂ + Cl₂ ↔ 2НCl при 25⁰С, якщо її тепловий ефект (Q_p) при цій температурі дорівнює 184446,7 Дж, а S^o_298(H2) = 130,5; S^o_298(Cl2) = 222,7; S^o_298(НCl) = 186,5 Дж/(моль К). Відповідь: 2,3 ∙ 10³³.

65. Визначити хімічну спорідненість і напрямок реакції СО + Н₂О ↔ СО₂ + Н₂ при одиничних концентраціях учасників реакції і температурах 1000 і 1200 К, якщо константи рівноваги К_р при цих температурах відповідно дорівнюють 1,39 і 0,71. Відповідь: -2,738 кДж; 3,417 кДж.

66. Константа рівноваги реакції СО + Н₂О ↔ СО₂ + Н₂ при 800 К дорівнює 4,12. В який бік піде реакція в суміші, склад якої (у мол.%) СО – 10; Н₂О – 20; СО₂ – 40; Н₂ – 30? Відповідь: ліворуч.

67. Константа рівноваги реакції СО + Н₂О ↔ СО₂ + Н₂ при 1500 К дорівнює 6,46. В який бік піде реакція в суміші, склад якої (у мол.%) СО – 30; Н₂О – 10; СО₂ – 40; Н₂ – 20? Відповідь: праворуч.

68. Константа рівноваги реакції А + В ↔ С + D, де всі учасники – гази, дорівнює при 1000 К 2,46. В який бік піде реакція в суміші, склад якої (у мол.%) А – 10; В – 20; С – 40; D – 30? Відповідь: ліворуч.

69. Визначити хімічну спорідненість заліза до кисню повітря (Р_О2 = 0,212 ∙ 10⁵ Па) при 1000 К, якщо константа рівноваги реакції 2Fe + O₂ ↔ 2FeO при цій температурі дорівнює 3,39 ∙ 10¹⁵ Па^-1. Відповідь: -380,1 кДж.

70. Тиск водяної пари над системою CuSO₄ ∙ 5H₂O ↔ CuSO₄ ∙ 3H₂O + 2H₂O при 308 К дорівнює 2,077 ∙ 10³ Па, а при 298 К – 0,98 ∙ 10³ Па. Визначити тепловий ефект цієї реакції (Q_p). Відповідь: -57,3 кДж.

71. Константа рівноваги (К_р ) реакції 2А + В = 2С при 800 К дорівнює 10^-16 . Обчислити К_р цієї реакції при 1000 К, якщо середнє значення теплового ефекту (Q_p) реакції дорівнює -480,6 кДж. Відповідь: 1,9 ∙ 10^-10 .

72. Визначити константу рівноваги реакції N₂ + 3H₂ ↔ 2NH₃ при 600 К на основі наступних даних: ∆S^х.р₂₉₈ = -198 Дж/К; ∆Н^х.р.₂₉₈ = -92,294 кДж; ∆С_р = 38,79 Дж/К. Відповідь: 1,23 ∙ 10^-2 .

73. Скориставшись діаграмою стану системи олово-цинк (рис. 1):

1) визначити масу і склад фаз, на які розпадається 10 кг 90%-ного за цинком розплаву, охолодженого до точки В;

2) яким станам системи (гомогенні чи гетерогенні) відповідають області, позначені римськими літерами. Які фази співіснують в цих областях?

3) Скільки ступенів свободи має система в точках 1-6?

II

IIІ

IV

I

1

2

6

4

5

3

B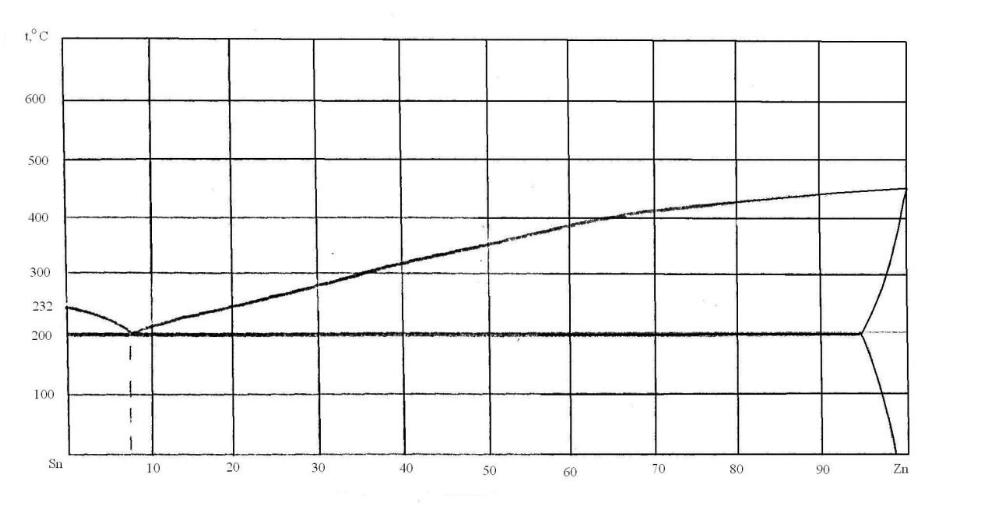

Рисунок 1 – Діаграма стану олово-цинк

74. Скориставшись діаграмою стану системи кадмій-цинк (рис.2):

1) визначити масу і склад фаз, на які розпадається 10 кг 90%-ного за цинком розплаву, охолодженого до точки В;

2) яким станам системи (гомогенні чи гетерогенні) відповідають області, позначені римськими літерами. Які фази співіснують в цих областях?

3) Скільки ступенів свободи має система в точках 1-6?

I

II

IIІ

В

IV

1

2

3

4

5

6

Рисунок 2 – Діаграма стану кадмій-цинк

75. Скориставшись діаграмою стану системи свинець-стибій (рис. 3):

1) визначити масу і склад фаз, на які розпадається 10 кг 90%-ного за сурьмою розплаву, охолодженого до точки В;

2) яким станам системи (гомогенні чи гетерогенні) відповідають області, позначені римськими літерами. Які фази співіснують в цих областях?

3) Скільки ступенів свободи має система в точках 1-6?

II

IV

IIІ

I

6

5

3

2

1

4

B

Рисунок 3 – Діаграма стану свинець-стибій

76. Скориставшись діаграмою стану системи алюміній-кремній (рис. 4):

1) визначити масу і склад фаз, на які розпадається 10 кг 90%-ного за кремнієм розплаву, охолодженого до точки В;

2) яким станам системи (гомогенні чи гетерогенні) відповідають області, позначені римськими літерами. Які фази співіснують в цих областях?

3) Скільки ступенів свободи має система в точках 1-6?

III

4

5

2

1

3

IV

II

I

B

6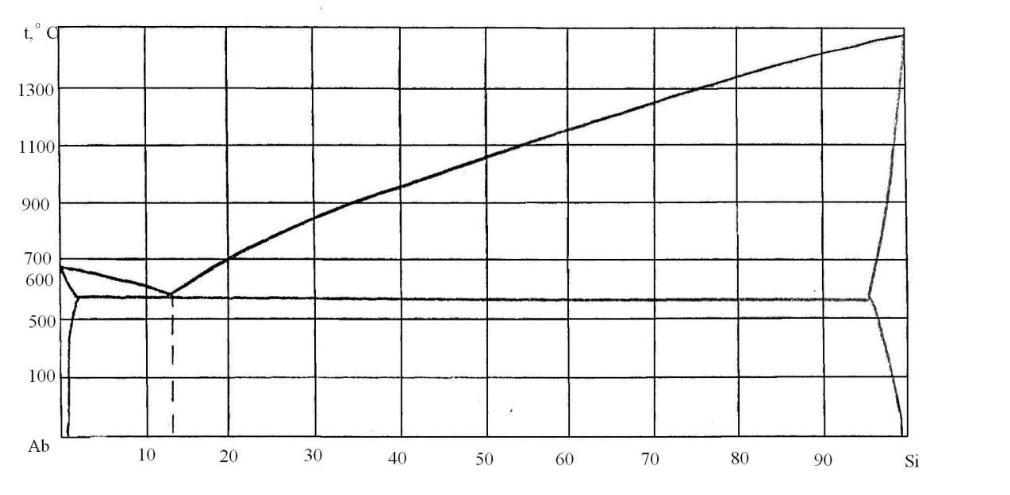

Рисунок 4 – Діаграма стану алюміній-кремній

77. Скориставшись діаграмою стану системи натрій-калій (рис. 5):

1) визначити масу і склад фаз, на які розпадається 10 кг 90%-ного за калієм розплаву, охолодженого до точки В;

2) яким станам системи (гомогенні чи гетерогенні) відповідають області, позначені римськими літерами. Які фази співіснують в цих областях?

3) Скільки ступенів свободи має система в точках 1-6?

III

5

6

3

IV

II

B

4

I

1

V

2

Рисунок 5 – Діаграма стану натрій-калій

78. Скориставшись діаграмою стану системи ртуть-кадмій (рис. 6):

1) визначити масу і склад фаз, на які розпадається 10 кг 20%-ного за ртуттю розплаву, охолодженого до точки В;

2) яким станам системи (гомогенні чи гетерогенні) відповідають області, позначені римськими літерами. Які фази співіснують в цих областях?

3) Скільки ступенів свободи має система в точках 1-6?

III

3

4

II

B

2

I

1

IV

5

6

V

Рисунок 6 – Діаграма стану ртуть-кадмій

79. Скориставшись діаграмою стану системи стибій-германій (рис. 7):

1) визначити масу і склад фаз, на які розпадається 10 кг 90%-ного за германієм розплаву, охолодженого до точки В;

2) яким станам системи (гомогенні чи гетерогенні) відповідають області, позначені римськими літерами. Які фази співіснують в цих областях?

3) Скільки ступенів свободи має система в точках 1-6?

III

5

3

1

I

B

6

II

2

IV

4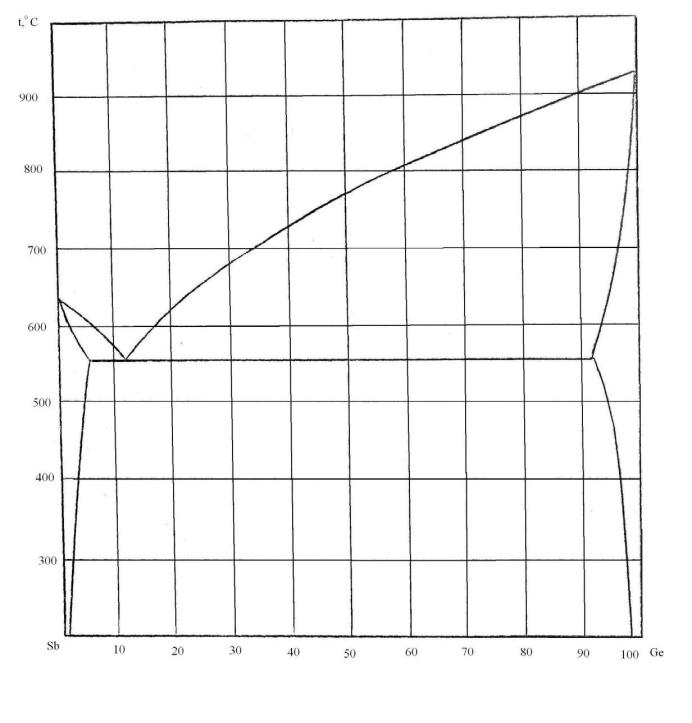

Рисунок 7 – Діаграма стану стибій-германій

80. Скориставшись діаграмою стану системи бісмут-стибій (рис. 8):

1) визначити масу і склад фаз, на які розпадається 10 кг 90%-ного за сурьмою розплаву, охолодженого до точки В;

2) яким станам системи (гомогенні чи гетерогенні) відповідають області, позначені римськими літерами. Які фази співіснують в цих областях?

3) Скільки ступенів свободи має система в точках 1-6?

III

5

6

3

II

B

4

I

2

IV

1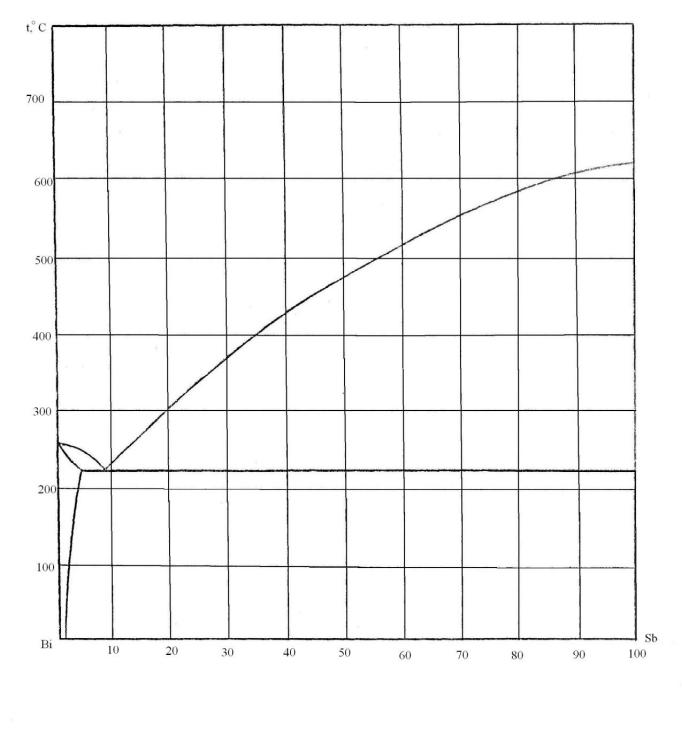

Рисунок 8 – Діаграма стану бісмут-стибій

81. Скориставшись діаграмою стану системи магній-германій (рис. 9):

1) визначити масу і склад фаз, на які розпадається 10 кг 90%-ного за германієм розплаву, охолодженого до точки В;

2) яким станам системи (гомогенні чи гетерогенні) відповідають області, позначені римськими літерами. Які фази співіснують в цих областях?

3) Скільки ступенів свободи має система в точках 1-6?

III

6

1

3

II

B

4

I

2

IV

V

5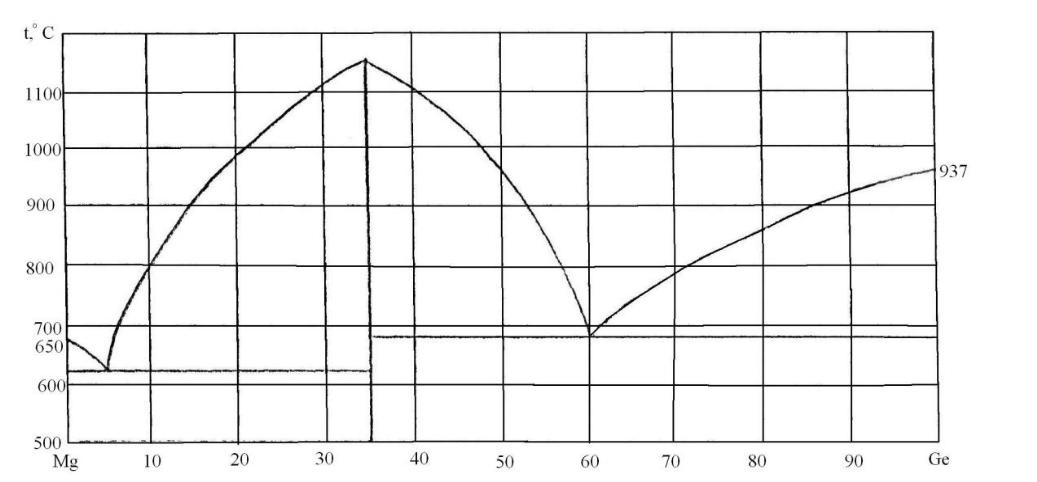

Рисунок 9 – Діаграма стану магній-германій

82. користавшись діаграмою стану системи магній-кальцій (рис. 10):

1) визначити масу і склад фаз, на які розпадається 10 кг 90%-ного за кальцієм розплаву, охолодженого до точки В;

2) яким станам системи (гомогенні чи гетерогенні) відповідають області, позначені римськими літерами. Які фази співіснують в цих областях?

3) Скільки ступенів свободи має система в точках 1-6?

III

5

1

6

I

B

3

4

II

2

IV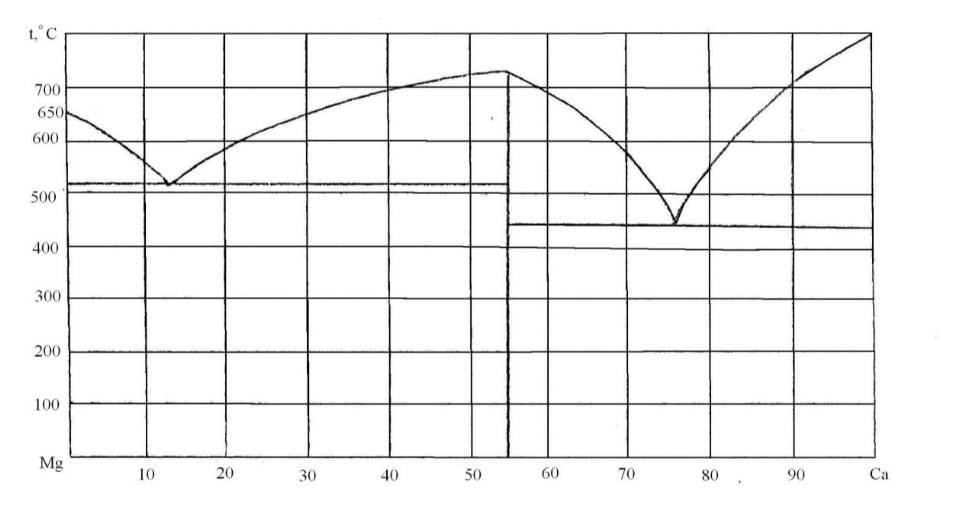

Рисунок 10 – Діаграма стану магній-кальцій

83.Скориставшись діаграмою стану системи алюміній-скандій (рис. 11):

1) визначити масу і склад фаз, на які розпадається 10 кг 80%-ного за скандієм розплаву, охолодженого до точки В;

2) яким станам системи (гомогенні чи гетерогенні) відповідають області, позначені римськими літерами. Які фази співіснують в цих областях?

3) Скільки ступенів свободи має система в точках 1-6?

III

5

6

3

II

B

2

I

4

IV

1

Рисунок 11 – Діаграма стану алюміній-скандій

84.Скориставшись діаграмою стану системи алюміній-барій (рис. 12):

1) визначити масу і склад фаз, на які розпадається 10 кг 90%-ного за барієм розплаву, охолодженого до точки В;

2) яким станам системи (гомогенні чи гетерогенні) відповідають області, позначені римськими літерами. Які фази співіснують в цих областях?

3) Скільки ступенів свободи має система в точках 1-6?

III

3

4

II

B

2

I

1

IV

5

6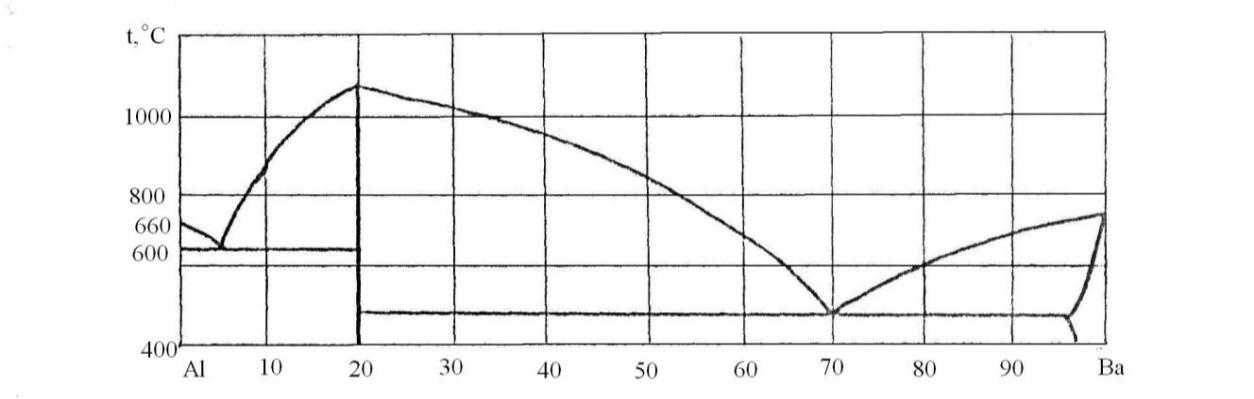

Рисунок 12 – Діаграма стану алюміній-барій

85. Скориставшись діаграмою стану системи вольфрам-гафній (рис. 13):

1) визначити масу і склад фаз, на які розпадається 10 кг 90%-ного за гафнієм розплаву, охолодженого до точки В;

2) яким станам системи (гомогенні чи гетерогенні) відповідають області, позначені римськими літерами. Які фази співіснують в цих областях?

3) Скільки ступенів свободи має система в точках 1-6?

III

5

6

3

II

B

4

I

2

IV

V

1

Рисунок 13 – Діаграма стану вольфрам-гафній

86. Скориставшись діаграмою стану системи алюміній-германій (рис. 14):

1) визначити масу і склад фаз, на які розпадається 10 кг 90%-ного за германієм розплаву, охолодженого до точки В;

2) яким станам системи (гомогенні чи гетерогенні) відповідають області, позначені римськими літерами. Які фази співіснують в цих областях?

3) Скільки ступенів свободи має система в точках 1-6?

III

6

5

1

II

B

4

I

2

IV

4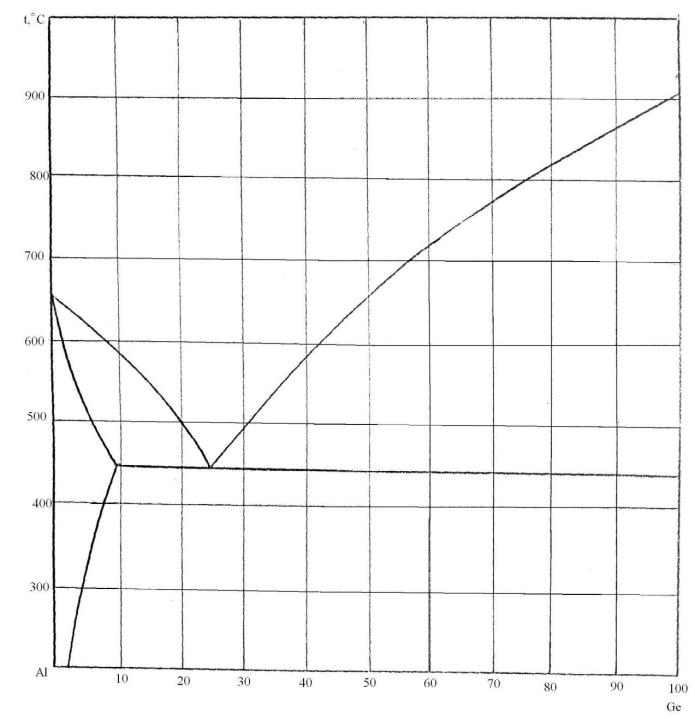

Рисунок 14 – Діаграма стану алюміній-германій

87. Скориставшись діаграмою стану системи мідь-срібло (рис. 15):

1) визначити масу і склад фаз, на які розпадається 10 кг 90%-ного за сріблом розплаву, охолодженого до точки В;

2) яким станам системи (гомогенні чи гетерогенні) відповідають області, позначені римськими літерами. Які фази співіснують в цих областях?

3) Скільки ступенів свободи має система в точках 1-6?

III

3

4

II

B

2

I

1

IV

5

6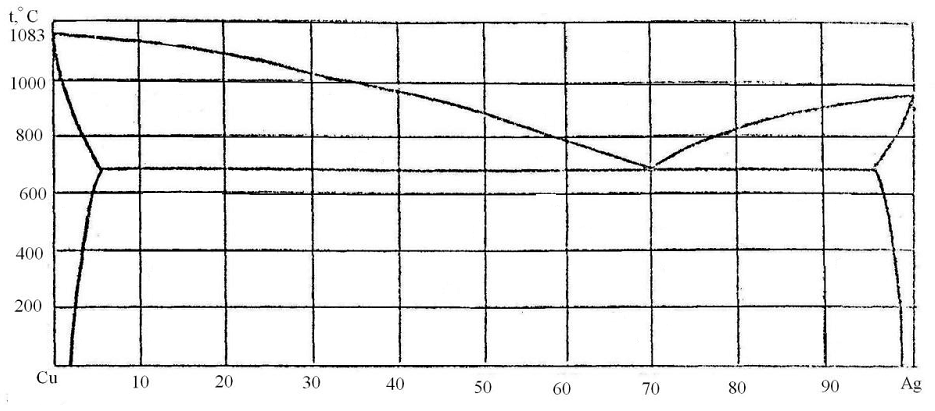

Рисунок 15 – Діаграма стану мідь-срібло

88. Скориставшись діаграмою стану системи титан-вольфрам (рис. 16):

1) визначити масу і склад фаз, на які розпадається 10 кг 90%-ного за вольфрамом розплаву, охолодженого до точки В;

2) яким станам системи (гомогенні чи гетерогенні) відповідають області, позначені римськими літерами. Які фази співіснують в цих областях?

3) Скільки ступенів свободи має система в точках 1-6?

III

3

4

II

B

2

IV

1

І

5

6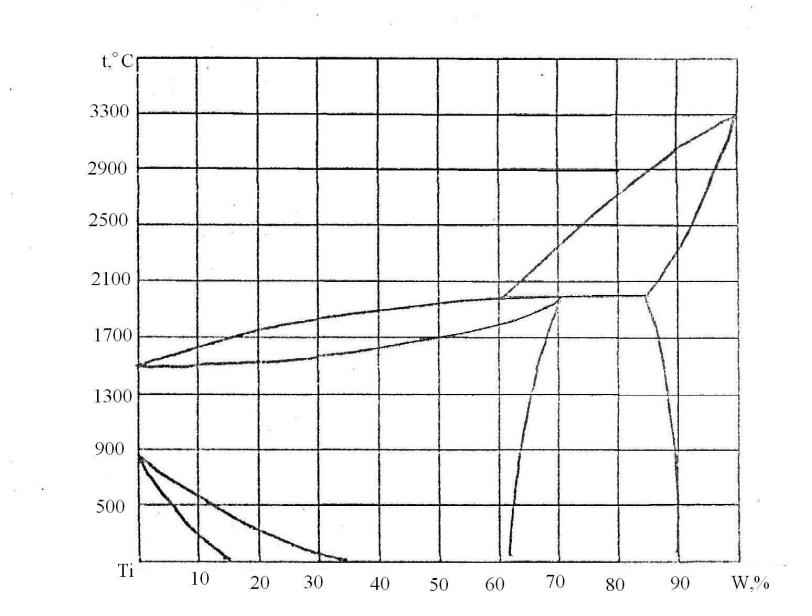

Рисунок 16 – Діаграма стану титан-вольфрам

89.Скориставшись діаграмою стану системи олово-цинк (рис. 17):

1) визначити масу і склад фаз, на які розпадається 10 кг 90%-ного за цинком розплаву, охолодженого до точки В;

2) яким станам системи (гомогенні чи гетерогенні) відповідають області, позначені римськими літерами. Які фази співіснують в цих областях?

3) Скільки ступенів свободи має система в точках 1-6?

III

5

4

II

B

2

I

1

IV

3

6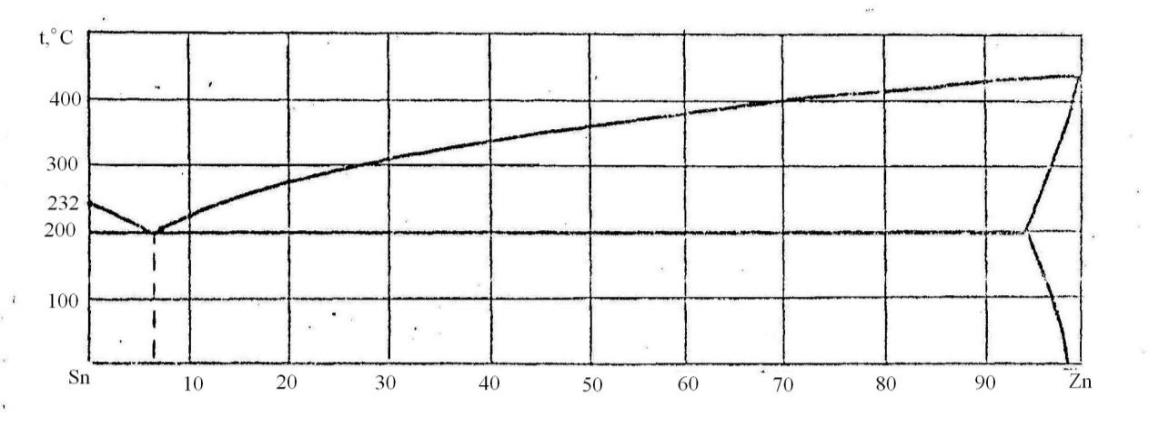

Рисунок 17 – Діаграма стану олово-цинк

90. Скориставшись діаграмою стану системи залізо-мідь (рис. 18):

1) визначити масу і склад фаз, на які розпадається 10 кг 20%-ного за залізом розплаву, охолодженого до точки В;

2) яким станам системи (гомогенні чи гетерогенні) відповідають області, позначені римськими літерами. Які фази співіснують в цих областях?

3) Скільки ступенів свободи має система в точках 1-6?

III

3

4

II

B

2

I

1

IV

5

6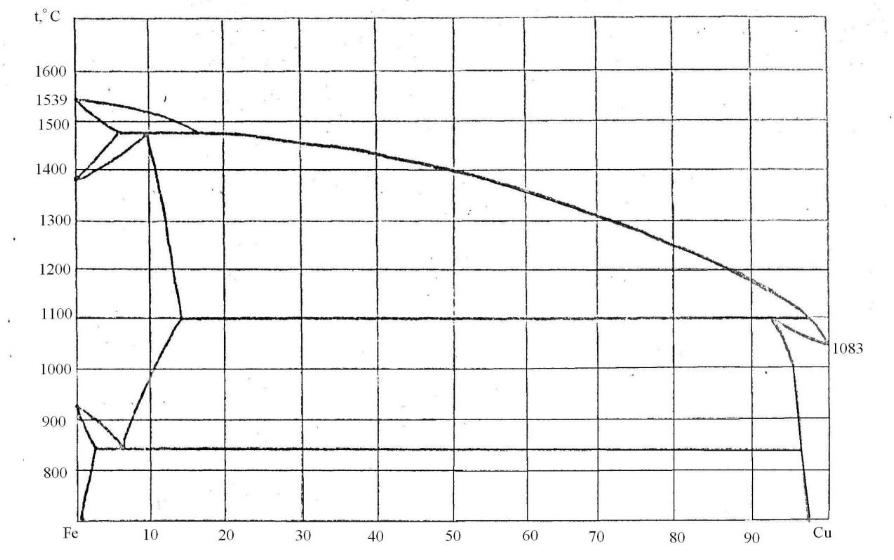

Рисунок 18 – Діаграма стану залізо-мідь

91. Скориставшись діаграмою стану системи свинець-магній (рис. 19):

1) визначити масу і склад фаз, на які розпадається 10 кг 90%-ного за магнієм розплаву, охолодженого до точки В;

2) яким станам системи (гомогенні чи гетерогенні) відповідають області, позначені римськими літерами. Які фази співіснують в цих областях?

3) Скільки ступенів свободи має система в точках 1-6?

III

3

4

II

B

2

I

1

IV

5

6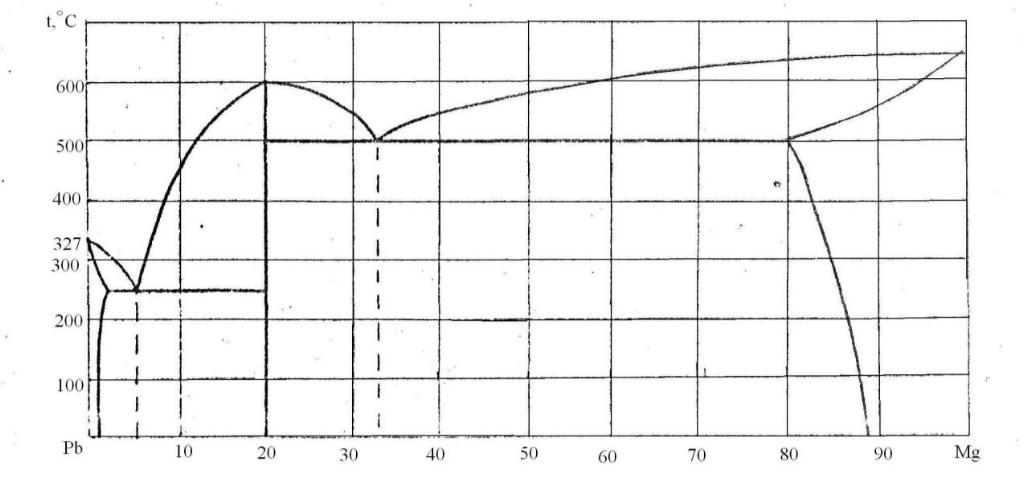

Рисунок 19 – Діаграма стану свинець-магній

92. Скориставшись діаграмою стану системи срібло-германій (рис. 20):

1) визначити масу і склад фаз, на які розпадається 10 кг 90%-ного за германієм розплаву, охолодженого до точки В;

2) яким станам системи (гомогенні чи гетерогенні) відповідають області, позначені римськими літерами. Які фази співіснують в цих областях?

3) Скільки ступенів свободи має система в точках 1-6?

III

3

4

II

B

2

I

1

IV

5

6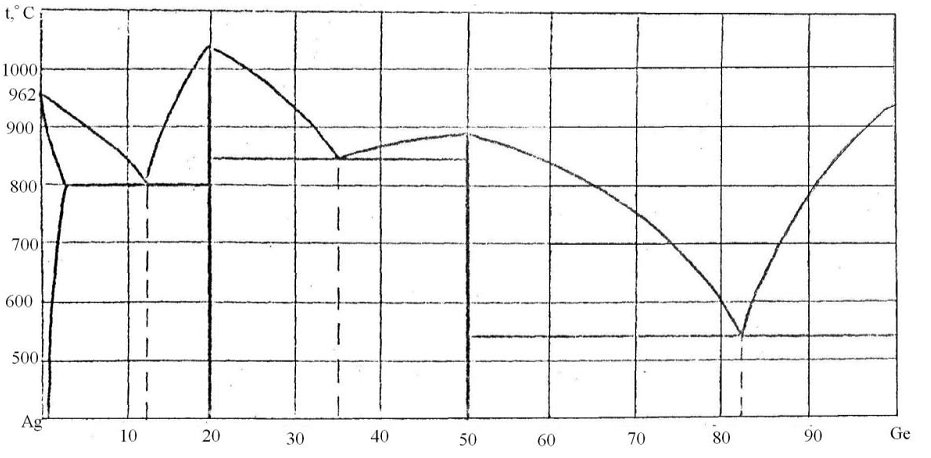

Рисунок 20 – Діаграма стану срібло-германій

93. Скориставшись діаграмою стану системи олово-цинк (рис. 21):

1) визначити масу і склад фаз, на які розпадається 10 кг 90%-ного за цинком розплаву, охолодженого до точки В;

2) яким станам системи (гомогенні чи гетерогенні) відповідають області, позначені римськими літерами. Які фази співіснують в цих областях?

3) Скільки ступенів свободи має система в точках 1-6?

III

3

4

II

B

2

I

1

IV

5

6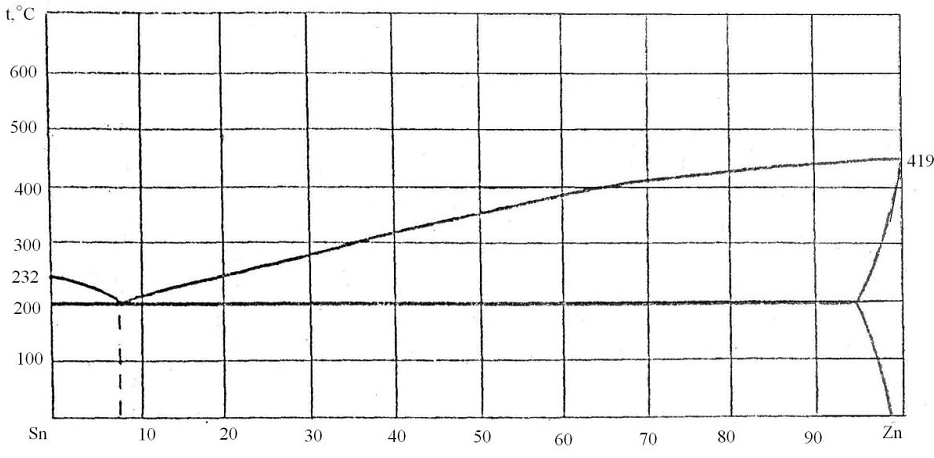

Рисунок 21 – Діаграма стану олово-цинк

94. Скориставшись діаграмою стану системи мідь-нікель (рис. 22):

1) визначити масу і склад фаз, на які розпадається 50 кг 70%-ного за міддю розплаву, охолодженого до точки В;

2) яким станам системи (гомогенні чи гетерогенні) відповідають області, позначені римськими літерами. Які фази співіснують в цих областях?

3) Скільки ступенів свободи має система в точках 1-6?

III

3

4

II

B

2

I

1

5

6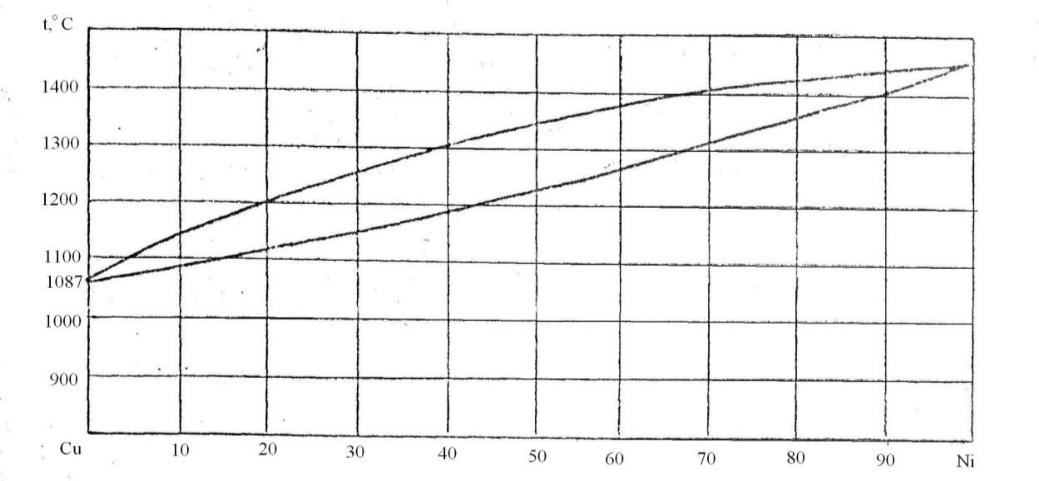

Рисунок 22 – Діаграма стану мідь-нікель

95. Скориставшись діаграмою стану системи сульфід заліза-сульфід марганцю (рис. 23):

1) визначити масу і склад фаз, на які розпадається 10 кг 80%-ного за сульфідом маганцю розплаву, охолодженого до точки В;

2) яким станам системи (гомогенні чи гетерогенні) відповідають області, позначені римськими літерами. Які фази співіснують в цих областях?

3) Скільки ступенів свободи має система в точках 1-6?

III

3

4

II

B

2

I

1

IV

5

6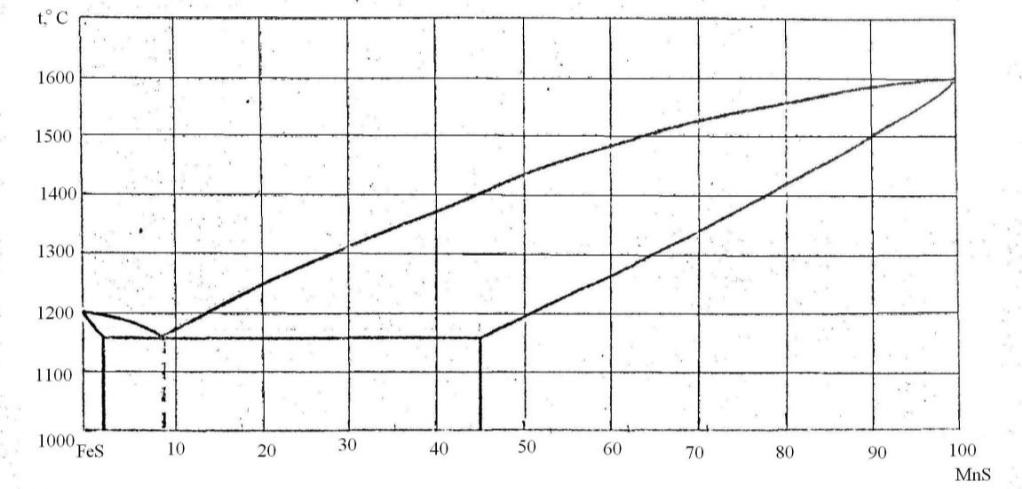

Рисунок 23 – Діаграма стану сульфід заліза-сульфід марганцю

96. Скориставшись діаграмою стану системи срібло-скандій (рис. 24):

1) визначити масу і склад фаз, на які розпадається 10 кг 90%-ного за скандієм розплаву, охолодженого до точки В;

2) яким станам системи (гомогенні чи гетерогенні) відповідають області, позначені римськими літерами. Які фази співіснують в цих облас

3) Скільки ступенів свободи має система в точках 1-6?

III

3

4

II

B

2

I

1

IV

5

6

V

Рисунок 24 – Діаграма стану срібло-скандій

97. Визначте температуру кипіння, температуру кристалізації і тиск насиченої пари при 25⁰С розчину, який вміщує 0,05 моль нелеткої біологічно активної речовини (неелектроліту) у 200 г води. Тиск насиченої пари води при 25⁰С дорівнює 3,167 кПа. Відповідь: 3,153 кПа.

98. Визначити масову частку водного розчину етиленгліколю, температура замерзання якого -0,5⁰С, маса води складає 200 г. Відповідь: 0,016.

99. При 30⁰С осмотичний тиск розчину, 100 мл якого вміщує 0,1778 г сечовини, дорівнює 74660 Па. Визначте молярну масу сечовини (концентрацію розрахувати в моль/м³).

Відповідь: 60 г/моль.

100. Розчин, який містить 0,785 г саліцилової кислоти у 20 г етанолу, кипить при температурі на 0,337⁰С вищій, ніж чистий спирт, ебуліоскопічна константа якого дорівнює 1,19⁰. Визначте молярну масу саліцилової кислоти. Відповідь: 138,6 г/моль.

101. Температура кипіння чистого CS₂ 319,2 К. Розчин, який містить 0,217 г сірки в 19,18 г CS₂ (ебуліоскопічна константа дорівнює 2,37⁰) кипить при 319,304 К. Визначте кількість атомів у молекулі сірки. Відповідь: 8.

102. Розчин, якій містить 0,12 г жовтого фосфору в 20 г сірковуглецю (ебуліоскопічна константа дорівнює 2,37⁰), закипає при температурі на 0,12⁰ вищій, ніж чистий розчинник. Розрахуйте, скільки атомів входить до складу молекули фосфору. Відповідь: 4.

103. Водний розчин містить 0,5% сечовини і 1% глюкози. Яка температура його кристалізації? Яка з розчинених речовин більше впливає на зниження температури кристалізації розчину? Відповідь: -0,262; сечовина.

104. Температура кипіння розбавленого водного глюкози вища за температуру кипіння води (ебуліоскопічна константа дорівнює 0,52⁰). Розрахуйте відносне зниження тиску насиченої пари води у цьому розчині (у %). Відповідь: 1,03%.

105. Розчин, який містить 0,345 г ацетаніліду С₆Н₅ОNС₂Н₃ у 25 г фенолу, кристалізується при 40,24⁰С. Визначте кріоскопічну сталу фенолу, якщо температура його кристалізації дорівнює 41⁰С. Відповідь: 7,43.

106. Відносне зниження тиску насиченої пари водного розчину, який містить 0,1 моль сахарози, становить 0,00189. Визначте осмотичний тиск розчину при 293 К. Густина розчину 1г/мл. (Концентрацію розрахувати в моль/м³). Відповідь: 2,5•10⁵ Па.

107. Визначте зниження температури замерзання крові, якщо її осмотичний тиск дорівнює 7,7•10⁵ Па при 310 К. При розв'язанні задачі прийміть, що молярність розчину дорівнює моляльності. Кріоскопічна константа розчинника дорівнює 1,86⁰. Відповідь: 0,56⁰.

108. Обчисліть температуру кипіння водного розчину (ебуліоскопічна константа дорівнює 0,52⁰) з масовою часткою новокаїну (М=272,8 г/моль) 2%, який використовують як місцевоанестезуючий засіб. Відповідь: 100,038⁰С.

109. Розрахуйте молярну масу органічної сполуки, якщо тиск насиченої пари розчину, який має в своєму складі 4,7 г сполуки в 100 г CCl₄, дорівнює при 20⁰С 11199 Па, а тиск насиченої пари CCl₄ становить 12132 Па. Відповідь: 86,8 г/моль.

110. Відносне зниження тиску пари водного розчину, який містить нелетку речовину становить 0,02. Визначте моляльність розчину. Відповідь: 1,134 моль/кг.

111. При Т=298 К тиск пари води дорівнює 3159,68 Н/м². Визначити, який тиск пари буде над водою, в якій масова частка гліцерину становить 10%. Відповідь: 3079,69 Н/м².

112. Питома теплота випаровування води при температурі кипіння дорівнює 2,464 Дж/г. Визначте температуру кипіння водного розчину, що містить 0,05 моль нелеткої розчиненої речовини в 200 г води. Відповідь: 373,128 К.

113. Водний розчин, що містить нелетку розчинену речовину замерзає при 271,5 К. Визначте температуру кипіння розчину і тиск його пари при 298 К. Кріоскопічна постійна для води 1,86, ебуліоскопічна константа - 0,523, тиск пари чистої при 298 К дорівнює 3167,21 Н/м². Відповідь: 3121,6 Н/м².

114. Розчинність кисню у воді при тиску 399,9•10² Н/м² і температурі 298 К дорівнює 16•10^-3 кг/м³. Визначити коефіцієнт Генрі. Відповідь: 4•10^-7 кг/Н•м.

115. Тиск насиченої пари розчинника над розчином 2,76 г деякої речовини в 100 г хлороформу при 298 К дорівнює 185,4 мм.рт.ст. Розрахувати молярну масу речовини, якщо при цій температурі тиск насиченої пари над індивідуальним хлороформом становить 196,8 мм.рт.ст. Відповідь: 53,5 г/моль.

116. Розрахувати ебуліоскопічну константу для бензолу, якщо його температура кипіння 353,25 К, а молярна теплота випаровування дорівнює 30,90 кДж/моль. Відповідь: 2,62.

117. При 22⁰С і тиску 390 мм.рт.ст. розчинність H₂S в аніліні дорівнює 10,6 г/л, а при 1160 мм.рт.ст. і тій же температурі 31,6 г/л. Чи виконується закон Генрі? Відповідь: так.

118. Змішали 0,5 моль речовини А з 0,3 моль речовини В при 27⁰С. Розрахувати зміну ентропії та зміну енергії Гіббса, якщо відомо, що речовини А і В утворюють доскональний розчин. Відповідь: 5,5Дж; -1651,2Дж.

119. Змішали 0,1 моль речовини А з 0,2 моль речовини В при 25⁰С. Розрахувати зміну ентропії та зміну енергії Гіббса, якщо відомо, що речовини А і В утворюють доскональний розчин. Відповідь: 1,59Дж; -473,5Дж.

120. CCl₄ та SnCl₄ утворюють ідеальний розчин. Визначити склад розчину (мольні частки), який кипить при 100⁰С під тиском 1 атм. Парціальні тиски парів CCl₄ та SnCl₄ при 100⁰С відповідно дорівнюють 1450 і 500 мм.рт.ст. Відповідь: 0,274; 0,726.

121. Розчин, який складається з бензолу та толуолу, містить 30% толуолу. Визначити загальгий тиск пари розчину і склад пари (у мольних частках). Тиск пари бензолу дорівнює 120,2 мм. рт. ст., а толуолу 36,7 мм. рт. ст. Відповідь: 97,91 мм.рт.ст.; 0,9; 0,1.

122. Тиск парів речовин А і В відповідно дорівнюють 350 і 760 мм. рт. ст. Визначити склад пари над розчином, отриманого змішуванням 0,5 моль А з 0,7 моль В. Відповідь: 0,248; 0,752.

123. При 50 ºС тиск пари бензолу дорівнює 269 мм. рт. ст., а тиск пари бромбензолу 17 мм. рт. ст. Чому дорівнюють мольні частки бензолу та бромбензолу в розчині, якщо мольна частка бензолу в парі становить 0,5. Відповідь: 0,94; 0,06.

124. Скільки грам гліцерину ( С₃Н₈О₃ ) потрібно розчинити у 200 г води, щоб відносне зниження тиску пари розчину склало на 10%? Відповідь: 113,5 г.

125. Скільки олова (в г.) потрібно розчинити в 50 г ртуті,щоб тиск пари ртуті понизився від 709,9 до 700 мм. рт. ст. Відповідь: 0,421 г.

126. Водний розчин кипить при 101 ºС. Чому дорівнює тиск розчинника над розчином, якщо тиск пари води дорівнює 787,5 мм. рт. ст., а мольна частка розчиненої речовини 0,043? Відповідь: 753,6 мм.рт.ст.

127. Розчинність кисню у воді при тиску 39997 Па і температурі 25⁰С дорівнює 16 мг/л. Визначити коефіцієнт Генрі (концентрацію кисню виразити в моль/м³). Відповідь: 79994.

128. При 25⁰С 1 літр води розчиняє 1 літр СО₂, якщо тиск СО₂ дорівнює 1 атм. Визначити молярність розчину, над яким тиск СО₂ при 25⁰С дорівнює 150 мм.рт.ст. Відповідь: 8,8•10^-3 моль/л.

129. Визначити зміну ентропії при змішуванні 100 г метилового спирту з 100 г етилового спирту, вважаючи що вони утворюють доскональний розчин. Відповідь: 29,85 Дж/(моль∙К).

130. С₆Н₆ та С₂Н₄Br утворюють доскональний розчин. Визначити: мольну частку бензолу в парах, якщо в розчині вона дорівнює 0,5; мольну частку бензолу в розчині, якщо в парах вона дорівнює 0,5. Тиск пари бензолу 269 мм.рт.ст., тиск пари диброметану 43 мм.рт.ст. Відповідь: 0,862; 0,138.

131. Змішали 0,2 моль речовини А та 0,5 моль речовини В при 20⁰С. Визначити зміну ентропії та вільної енергії, якщо відомо, що речовини А та В утворюють доскональний розчин. Відповідь: 3,475 Дж/(моль∙К);

-1018,175 Дж.

132. Тиск пари розчину, що містить 13 г нелеткої розчиненої речовини в 100 г Н₂О при 28⁰С дорівнює 27,371 мм.рт.ст. Розрахувати молекулярну масу розчиненої речовини (розчин ідеальний). Тиск пари води при 28⁰С дорівнює 28,065 мм.рт.ст. Відповідь: 92,5.

133. Відносне зниження тиску пари водного розчину, який містить нелетку речовину становить 0,04. Визначте моляльність розчину. Відповідь: 2,315 моль/кг.

134. Відносне зниження тиску пари водного розчину, який містить нелетку речовину становить 0,01. Визначте моляльність розчину. Відповідь: 0,56 моль/кг.

135. Значення похідної dP/dT насиченої пари диетилового етеру при нормальному атмосферному тиску і температурі кипіння 307,9 К дорівнює 3,53•10³ Н/(м²∙К). Обчислити теплоту випаровування за рівнянням Клаузіуса-Клапейрона. Відповідь: 2,74•10⁴ Дж/моль.

136. Питома теплота випаровування води при температурі кипіння дорівнює 2,252•10³ Дж/кг. Визначити температуру кипіння водного розчину, що містить 0,02 моль нелеткої розчиненої речовини в 400 г води. Відповідь: 373,026 К.

137. Визначити температуру замерзання 10%-го водного розчину сечовини (СО(NH₂)₂). Кріоскопічна стала води дорівнює 1,86⁰. Відповідь: -3,44⁰С.

138. Знайдіть зміну тиску пари води при збільшенні температури на один градус поблизу температури кипіння при нормальному атмосферному тиску. Теплота випаровування води при температурі кипіння при тиску 101,325 кПа дорівнює 2255,1 кДж/кг. Відповідь: 3,56∙10³ Па.

139. Розрахуйте молярну теплоту випаровування диетилового ефіру, що застосовується для інгаляційного наркозу, якщо поблизу температури кипіння (307,9 К) при тиску 101325 Па dp/dT = 3,53∙10³ Па/К. Відповідь: 27,5 кДж/моль.

140. Визначте тиск насиченої пари пентанолу-3, що використовується у синтезі вітамінів А та Е, при 357 К, якщо при 347 К тиск насиченої пари дорівнює 43,316 кПа, а теплота випаровування його у цьому інтервалі температур становить 34,9 кДж/моль. Відповідь: 60,65 кПа.

141. Тиск пари чистого бензолу при 60⁰С становить 385 мм.рт.ст., а чистого толуолу 139 мм.рт.ст. Розрахувати парціальні тиски бензолу і толуолу, загальний тиск пари розчину, якщо молярна частка толуолу складає 0,6. Відповідь: 154 мм.рт.ст., 83,4 мм.рт.ст., 237,4 мм.рт.ст.

142. При 25⁰С тиск пари CCl₄ становить 143 мм.рт.ст., а хлороформу 199 мм.рт.ст. Рідини утворюють ідеальний розчин. Який буде загальний тиск пари над розчином, якщо змішати 1 моль CCl₄ та 3 моля CHCl₃ та якою буде молярна частка CCl₄ в парі? Відповідь: 185 мм.рт.ст.; 0,193.

143. Осмотичний тиск глюкози при 40⁰С дорівнює 950 мм.рт.ст. Яка маса глюкози у 500 мл розчину? Відповідь: 4,41г.

144. Розрахуйте температуру, при якій тиск насиченої пари етиленгліколю дорівнює 109072,2 Па, якщо температура випаровування при атмосферному тиску дорівнює 197,3⁰С, а ∆Н_вип.= 50,5 кДж/моль. Відповідь: 200⁰С.

145. Водний розчин хлориду амонію, моляльність якого 0,1, замерзає при -0,344^оС. Визначити його температуру кипіння, якщо для води К_к = 1,86 і К_є = 0,51. Відповідь: 100,094^оС.

146. Водний розчин сульфату калію, моляльність якого 0,4, замерзає при -1,52^оС. Вважаючи, що і не залежить від температури, визначити тиск пари розчину при 20^оС і його температуру кипіння. Тиск пари води при 20^оС дорівнює 2,34 кПа, К_к = 1,86 і К_є = 0,51. Відповідь: 2,30 кПа; 100,417^оС.

147. Тиск пари води над розчином, що містить 6,41 г хлориду магнію в 100 г води, дорівнює 98,12 кПа при 100^оС . Визначити температуру кипіння цього розчину, якщо К_є = 0,51. Відповідь: 100,9^оС.

147. При 25^оС тиск пари водного розчину CoCl₂, моляльність якого 2, дорівнює 2,666 кПа. Тиск пари водного розчину гліцерину при тій же моляльності дорівнює 2,973 кПа. Тиск пари води дорівнює 3,167 кПа. Знайти осмотичний коефіцієнт CoCl₂ в розчині. Відповідь: 0,858.

147. Водний розчин K₃Fe(CN)₆, моляльність якого 0,01, замерзає при -0,062^оС. Визначити осмотичний коефіцієнт, якщо К_к = 1,86. Відповідь: 0,833.

147. Водний розчин хлориду калію, що містить 14.92 г KCl в 100 г води, замерзає при -0,68^оС. Визначити осмотичний і ізотонічний коефіцієнти, якщо К_к = 1,86. Відповідь: 0,914; 1,828.

147. Розчин, що містить 2,45 г H₂SO₄ в 500 г води, замерзає при -0,2055^оС. Кріоскопічна константа води дорівнює 1,86. Визначити осмотичний і ізотонічний коефіцієнти. Відповідь: 0,737; 2,21.

147. Визначити активність HCl в водному розчині при моляльності 0,02, якщо відомо, що середній коефіцієнт активності HCl дорівнює 0,894. Відповідь: 3,197 · 10^-4.

147. Визначити активність і середню активність сульфату цинку в 0,1 моляльному розчині, якщо f_± = 0,148. Відповідь: 2,19 · 10^-4; 1,48 · 10^-2.

147. Визначити активність La(NO₃)₃ в 0,01-моляльному розчині, якщо f_± = 0,148. Відповідь: 2,87 · 10^-8.

147. Середній коефіцієнт активності KCl в 0,01-моляльному розчині дорівнює 0,922. Середній коефіцієнт активності KNO₃ в 0,01-моляльному розчині дорівнює 0,916. Визначити коефіцієнт активності іону NO₃^-, якщо f_K+ = f_Cl-. Відповідь: 0,91.

147. Визначити іонну силу розчину, що містить 0,01 моль H₂SO₄ і 0,02 моль MgSO₄ в 1000 г води. Відповідь: 0,11.

147. За допомогою граничного закону Дебая-Гюккеля знайти середній коефіцієнт активності K₃Fe(CN)₆ в розчині, моляльність якого 0,001, якщо h = 0,51. Відповідь: 0,762.

147. Визначити активність і середню активність H₂SO₄ в 0,1-моляльному розчині, якщо середній коефіцієнт активності H₂SO₄ дорівнює 0,265. Відповідь: 7,44 · 10^-5; 4,21 · 10^-2.

147. За допомогою граничного закону Дебая-Гюккеля визначити середній коефіцієнт активності хлориду цинку в його 0,005-моляльному розчині. Відповідь: 0,75.

147. Визначити константу гідролізу хлориду амонію і рН його водного розчину при концентрації 10^-4 моль/кг, якщо К_сл.о гідроксиду амонію дорівнює 1,8 · 10^-5. Відповідь: 5,6 · 10^-10; 6,63.

147. Визначити константу гідролізу ацетату калію і рН його водного розчину при концентрації 0,01 моль/кг і 25^оС, якщо константа дисоціації оцтової кислоти дорівнює 1,75 · 10^-5. Відповідь: 5,7 · 10^-10; 10,76.

147. Водний розчин з моляльною концентрацією хлориду кальцію, рівною 0,3, має температуру кипіння 100,4^оС. Визначити ступінь дисоціації хлориду кальцію. Ебуліоскопічна стала води складає 0,51. Відповідь: 0,805.

147. Скільки грамів КОН треба розчинити в 200 мл води, щоб одержати розчин із ступенем дисоціації 0,9 і температурою замерзання -0,8^оС, якщо кріоскопічна стала = 1,86. Відповідь: 2,53.

147. При якому розведенні концентрація іонів ОН^- в водному розчині гідроксиду амонію буде дорівнювати 10^-3 моль/л? Концентраційна константа дисоціації гідроксиду дорівнює 1,8 · 10^-5. Відповідь: 18 л/моль.

147. При якому розведенні рН водного розчину хлоратної (І) кислоти буде дорівнювати 4? Концентраційна константа дисоціації кислоти дорівнює 5,8 · 10^-8. Відповідь: 5,8 л/моль.

147. Концентраційна константа дисоціації ціанідної кислоти в водному розчині при 25^оС дорівнює 7,9 · 10^-10. При якій концентрації кислоти її ступінь дисоціації дорівнює 0,001, яке рН цього розчину? Відповідь: 7,89 · 10^-4; 6,1.

147. Обчислити іонну силу водного розчину, який в 10 мл містить 10^-4 моль гідроксиду барію, якщо ступінь дисоціації дорівнює 0,8. Відповідь: 0,024.

147. Обчислити іонну силу водного розчину, який в 100 мл містить 0,01 моль сульфату калію, хрому (ІІІ). Ступінь дисоціації прийняти рівним 1. Відповідь: 0,9.

147. При пропусканні струму силою 3 А протягом 28 хв. 42 с через водний розчин нітрату двовалентного металу на катоді виділилось 1,75 г металу. Що це за метал? Скільки речовини (в грамах) виділилось на графітовому аноді? Відповідь: цинк; 0,43 г.

147. При електролізі водного розчину нітрату мангану (ІІ) на одному з інертних електродів виділилось 0,549 г металу. Який об’єм газу виділився на іншому електроді, якщо вихід за струмом при виділенні газу 80%? Відповідь: 89,6 мл.

147. При електролізі водного розчину нітрату літію на інертному аноді виділилось 2,24 л газу. Скільки (в грамах) речовини утворилося на катоді і біля катоду, якщо катодний вихід за струмом складає 90%? Відповідь: 0,36 г; 8,64 г.

147. При електролізі водних розчинів CaCl₂ I CuSO₄, сполучених послідовно з джерелом струму, на одному з катодів виділилось 1,12 л газу. Скільки грамів речовини виділиться на іншому катоді; на інертних анодах, якщо вихід за струмом дорівнює 100%? Відповідь: 3,18 г; 3,55 г; 0,80 г.

147. Скільки грамів нітратної кислоти утвориться біля інертного аноду при електролізі водного розчину нітрату калію, якщо на аноді виділилось 448 мл кисню при анодному виході за струмом 80%. Обчислити масу речовини, що виділиться на катоді. Відповідь: 6,3 г; 0,1 г.

147. Чому дорівнюють катодний і анодний виходи за струмом при електролізі водного розчину сульфату натрію на графітових електродах, якщо було пропущено 9650 Кл електрики, а на катоді і аноді виділилось, відповідно, 896 і 504 мл газів? Відповідь: 80%; 90%.

147. Обчислити напругу розкладу водного розчину сульфату кадмію на платинових електродах, якщо перенапруга кисню на аноді дорівнює 0,45 В. Стандартні потенціали потенціали кадмію і кисню відповідно дорівнюють -0,403 В і 1,229 В. Перенапругою кадмію на катоді знехтувати. Відповідь: 2,082 В.

147. Визначити величину перенапруги водню на свинцевому катоді, якщо при електролізі водного розчину сульфатної кислоти з платиновим анодом напруга розкладу дорівнює 2,69 В. Перенапругу кисню на платиновому електроді вважати такою, що дорівнює 0,45 В, стандартний потенціал кисню дорівнює 1,229 В. Відповідь: 1,011 В.

147. Питома електропровідність розчину слабкої одноосновної кислоти з молярною масою 60 г/моль і ступенем дисоціації 0,1 при 25^оС дорівнює 0,012 См/см. Знайти еквівалентну електропровідність розчину, якщо його концентрація 10%, а густина 1,116 г/см³. Відповідь: 64,5 См ^. см²/моль.

147. Знайти масову частку розчину сульфатної кислоти з густиною 1,03 г/см³, якщо питома і еквівалентна електропровідності розчину відповідно дорівнюють 0,214 См/см і 240 См ^. см²/моль. Відповідь: 0,042 (4,2 %).

147. Молярна електропровідність розчину хлориду алюмінію, що містить в 50 мл 1,335 г солі при 25^оС дорівнює 142,8 См ^. см²/моль. Обчислити питому та еквівалентну електропровідності при цій температурі, прийнявши α = 0,9. Відповідь: 2,57 ^. 10^-2 См/см; 47,6 См ^. см²/моль.

147. Еквівалентна електропровідність 0,1 М розчину оцтової кислоти при 18^оС дорівнює 39,5 См ^. см²/моль. Обчислити питому електропровідність, ступінь дисоціації і рН розчину, якщо λ^о_Н+ = 353,8 См ^. см²/моль і λ^о _СН3СОО- = 40,9 См ^. см²/моль. Відповідь: 3,95 ^. 10^-4 См/см; 0,1; 2.

147. Еквівалентна електропровідність розчину оцтової кислоти з концентрацією 1,62 ммоль/л при 18^оС дорівнює 39,5 См ^. см²/моль. Обчислити ступінь дисоціації кислоти, питому електропровідність розчину, його рН і константу дисоціації, якщо λ^о _СН3СОО- = 40,9 і λ^о_Н+ = 353,8 См ^. см²/моль. Відповідь: 0,1; 6,4 ^. 10^-6 См/см; 5,8; 1,8 ^. 10^-5.

147. Обчислити еквівалентну електропровідність розчину нітрату рубідію при нескінченному розведенні, якщо значення цієї величини для хлорату (VІІ) рубідію, нітрату калію і хлорату (VІІ) калію при 25^оС відповідно рівні: 145,5; 144,9; 141,5 См ^. см²/моль. Відповідь: 148,9 См ^. см²/моль.

147. Обчислити еквівалентну електропровідність розчину броміду цезію при нескінченному розведенні, якщо значення цієї величини для нітрату цезію, нітрату літію і броміду літію при 25^оС відповідно дорівнюють: 148,2; 110,1; 117,0 См ^. см²/моль. Відповідь: 155,1 См ^. см²/моль.

147. Обчислити числа переносу іонів Zn²⁺ I NO₃^- в 0,02 М розчині Zn(NO₃)₂ на основі таких даних: об’єм католіту 65 мл; маса цинку в ньому після електролізу 0,06 г; маса срібла, що виділилось на катоді кулонометра 0,15 г. Відповідь: 0,55; 0,45.

147. В результаті електролізу розчину сульфату нікелю (ІІ) між нікелевими електродами на катоді виділилося 0,2 г нікелю при 100%-му його виході за струмом. До електролізу розчин біля аноду містив 1,15 г Ni²⁺, а після – 1,30 г Ni²⁺. Знайти числа переносу іонів Ni²⁺ і SO₄^2-.

147. В розчині хлориду амонію число переносу аніону дорівнює 0,491. Знайти абсолютну швидкість і рухливість катіону в нескінченно розбавленому розчині, якщо еквівалентна електропровідність розчину при нескінченному розведенні дорівнює 149 См ^. см²/моль. Відповідь: 7,86 ^. 10^-4 см^{2 .} с^{-1 .} В^-1; 75,84 См ^. см²/моль.

147. В розчині нітрату натрію число переносу аніону дорівнює 0,47. Знайти абсолютну швидкість і рухливість катіону в нескінченно розбавленому розчині, якщо еквівалентна електропровідність розчину при нескінченному розведенні дорівнює 126 См ^. см²/моль. Відповідь: 6,92 ^. 10^-4 см^{2 .} с^{-1 .} В^-1; 66,78 См ^. см²/моль.

147. Розрахувати абсолютну швидкість руху однозарядного іону радіусом 0,1 нм у воді, в’язкість якої при 25^оС дорівнює 0,894 ^. 10^-3 Па ^. с. Застосовуючи правило Вальдена-Писаржевського, обчислити швидкість руху цього іону в гліцерині, який має при тій же температурі в’язкість 1,49 Па ^. с. Відповідь: 9,5 ^. 10^-8 м^{2 .} с^{-1 .} В^-1; 5,7 ^. 10^-11 м^{2 .} с^{-1 .} В^-1.

147. Розрахувати абсолютну швидкість руху однозарядного іону з радіусом 0,1 нм в форма міді, в’язкість якого дорівнює 3,31 ^. 10^-3 Па ^. с при 25^оС. Виходячи з правила Вальдена-Писаржевського, обчислити абсолютну швидкість руху цього іону в метилацетаті, який має при тій же температурі в’язкість, рівну 0,344 ^. 10^-3 Па ^. с. Відповідь: 2,57^. 10^-8 м^{2 .} с^{-1 .} В^-1; 2,47 ^. 10^-7 м^{2 .} с^{-1 .} В^-1.

147. Розрахувати радіус „за Стоксом” однозарядного іону, якщо його рухливість в нескінченно розбавленому водному розчині при 25^оС дорівнює 38,7 ^. 10^-4 См ^. м²/моль, а в’язкість води при цій температурі дорівнює 0,894 ^. 10^-3 Па ^. с. Оцінити рухливість цього іону при нескінченному розведенні в гліцерині, в’язкість якого дорівнює 1,49 Па ^. с. Відповідь: 2,37 ^. 10^-10 м; 23,22 ^. 10^-7 См ^. м²/моль.

147. Коефіцієнт дифузіі іонів літію в водному розчині дорівнює 1,04 ^. 10^-9 м²/с. Визначити коефіцієнт дифузії літію в метилацетаті, в’язкість якого дорівнює 0,362 ^. 10^-3 Па ^. с, якщо в’язкість води дорівнює 0,894 ^. 10^-3 Па ^. с. Відповідь: 2,57 ^. 10^-9 м²/с.

147. Рухливість двозарядного іону в нескінченно розбавленому водному розчині при 25^оС дорівнює 76,3 См ^. см²/моль, а в’язкість води при цій температурі дорівнює 0,894 ^. 10^-3 Па ^. с. Розрахувати коефіцієнт дифузії цього іону при 25^оС у воді і ацетонітрилі, в’язкість якого дорівнює 0,35 ^. 10^-3 Па ^. с. Відповідь: 1,01 ^. 10^-5 см²/с; 2,59 ^. 10^-5 см²/с.

147. Обчислити константу рівноваги реакції, що протікає в елементі Fe | Fe²⁺ || Ni²⁺ | Ni при 298 К, якщо а_Fe2+ = 0,1 і а_Ni2+ = 0,01 моль/л. Відповідь: 2,75 ^. 10⁵.

147. Обчислити константу рівноваги реакції, що протікає в елементі Cu | Cu²⁺ || Ag⁺ | Ag при 298 К, якщо а_Cu2+ = 0,2 і а_Ag+ = 0,1 моль/л. Відповідь: 1,77 ^. 10¹⁴.

147. В гальванічному елементі при 298 К протікає реакція Zn + 2Ag⁺ = 2Ag + Zn²⁺. Знайти зміну ентропії реакції, якщо е.р.с. елементу дорівнює 1,562 В, а стандартні ∆Н^о утворення Zn²⁺ і Ag⁺ дорівнюють -152,4 і 105,9 кДж/моль, відповідно. Відповідь: - 210,5 Дж/моль К.

147. В гальванічному елементі Zn | Zn²⁺ || Ni²⁺ | Ni протікає струмоутворююча реакція. Розрахувати її тепловий ефект (∆Н), якщо а_Zn2+ = 0,01 і а_Ni2+ = 0,0001 моль/л і ентропії утворення Zn, Zn²⁺, Ni²⁺ і Ni відповідно дорівнюють: 41,62; -106,5; -159,4; 30,12 Дж/моль К. Відповідь: -75,28 кДж

147. В гальванічному елементі Al | Al³⁺ || Ag⁺ | Ag протікає струмоутворююча реакція. Розрахувати її тепловий ефект (∆Н), якщо а_Al3+ = 0,001 і а_Ag+ = 0,1 моль/л і ентропії утворення Al , Al³⁺ , Ag⁺ і Ag відповідно дорівнюють 28,32; -313,3; 73,92; 42,70 Дж/моль К. Відповідь: -842,17 кДж.

147. Е.р.с. елементу, в якому протікає реакція Ag + ½ Hg₂Cl₂ = AgCl + Hg дорівнює 0,0456 В при 298 К і 0,0439 при 293 К. Знайти стандартні значення ∆G, ∆H I ∆S. Відповідь: 4,4 кДж; 5,374 кДж; 32,8 Дж/моль К.

147. Обчислити тепловий ефект (Q_p) і зміну ентропії реакції Cd + PbCl₂ = CdCl₂ + Pb, що протікає в гальванічному елементі при 298 К, якщо е.р.с. елементу дорівнює 0,188 В, а температурний коефіцієнт дорівнює -4,8 ^. 10^-4 В ^. К^-1. Відповідь: 63,89 кДж.

147. Тепловий ефект (Q_p) реакції Pb + 2AgCl = PbCl₂ + 2Ag дорівнює 105,1 кДж. Е.р.с. елементу, працюючого за рахунок цієї реакції дорівнює 0,7901 В при 298 К. Обчислити е.р.с. елементу при 293 К. Відповідь: 0,491 В.

147. Тепловий ефект (Q_p) реакції Pb + Hg₂Cl₂ = PbCl₂ + 2Hg дорівнює 94,2 кДж при 298 К. Е.р.с. елементу, в якому оборотно протікає ця реакція, зростає на 1,45 ^. 10^-4 В при підвищенні температури на 1 К. Обчислити е.р.с. елементу і зміну ентропії при 298 К. Відповідь: 0,5313 В; 27,99 Дж/моль К.

147. Константа рівноваги реакції 2Cl₂ + 2H₂O = O₂ + 4Cl^- + 4H⁺ при 298 К дорівнює 1,122 ^. 10⁹ . Обчислити зміну енергії Гіббса в ході реакції і стандартну е.р.с. для елемента, в якому оборотно протікає така реакція. Відповідь: -51,5 кДж; 0,133 В.

147. Обчислити при 298 К е.р.с. концентраційного гальванічного елементу, в якому електродами служать цинкові амальгами з активностями цинку в них, відповідно, 33,65 ^. 10^-4 і 11,3 ^. 10^-5 моль/л, а електролітом – розчин хлориду цинку. Відповідь: 43,5 Мв.

147. Розрахувати е.р.с. елементу, що складається з двох водневих електродів, опущених в розчини з pH, рівними 3,5 і 6,5. Відповідь: 0,177 В.

147. Яка е.р.с. гальванічного елементу, що складається з цинкових електродів, опущених в 0,01 М і 0,0001 М розчини солі цинку із ступенями дисоціації 0,8 і 0,9, відповідно? Відповідь: 57,5 Мв.

147. Обчислити ступінь дисоціації солі цинку в 1 М розчині, якщо потенціал цинку в цьому розчині дорівнює -0,77 В. Відповідь: 0,46 .

147. Гальванічний елемент складається із стандартного водневого електроду і інертного електроду, вміщеного в 0,1 М розчин одноосновної слабкої кислоти. Е.р.с. елементу дорівнює 0,1 В. Обчислити pH розчину і константу дисоціації кислоти. Відповідь: 5 ^. 10^-3.

147. Визначити при 298 К е.р.с. концентраційного гальванічного елементу, в якому електродами служать мідні амальгами з активностями міді в них, відповідно, 26,63 ^. 10^-3 і 8,22 ^. 10^-5 моль/л, а електролітом – сульфат купруму (ІІ). Відповідь: 74,1 Мв.

147. Гальванічний елемент складається із стандартного водневого електроду і інертного електроду, вміщеного в 0,02 М розчин одноосновної слабкої кислоти. Е.р.с. елементу дорівнює 0,2 В Обчислити pH розчину і константу дисоціації кислоти. Відповідь: 3,4; 8,16 ^. 10^-6.

147. Обчислити ступінь дисоціації солі купруму (ІІ) в 1 М розчині, якщо потенціал міді в цьому розчині дорівнює 0,33 В. Відповідь: 0,46.

147. Чому дорівнює е.р.с. гальванічного елементу, що складається із срібних електродів, які опущені в 0,1 і 0,001 М розчини солей аргентуму із ступенями дисоціації 0,7 і 0,9, відповідно? Відповідь: 111,56 Мв.

147. Розрахувати константу дисоціації солі нікелю в 0,01 М розчині, якщо потенціал нікелю в цьому розчині дорівнює -0,35 В. Відповідь: 1,67 ^. 10^-5.

147. Знайти константу рівноваги реакції, що протікає за стандартних умов в гальванічному елементі Zn | Zn²⁺ || Ni²⁺ | Ni. Відповідь: 2 ^. 10¹⁷.

147. Тепловий ефект (Q_p) реакції, що протікає в гальванічному елементі Ме₁⁰ | Ме₁⁺ || Ме₂⁺ | Ме₂⁰ дорівнює 5,4 кДж. Е.р.с. елементу при 298 К дорівнює 0,050 В. Обчислити його е.р.с. при 20^оС. Відповідь: 50 Мв.

147. Обчислити константу рівноваги реакції, що протікає в елементі Zn | Zn²⁺|| Ag⁺ | Ag при 298 К, якщо активності іонів цинку і аргентуму відповідно рівні 0,01 і 0,1 моль/л. Відповідь: 7,94 ^. 10⁵².

147. Обчислити тепловий ефект (Q_p) і зміну ентропії реакції Co + CuSO₄ = CoSO₄ + Cu, що протікає в гальванічному елементі при 298 К, якщо е.р.с. елементу 0,548 В, а температурний коефіцієнт 1,08 ^. 10^-4 В ^. К^-1. Відповідь: 99,55 кДж; 20,84 Дж/моль К.

147. При синтезі фосгену встановилась хімічна рівновага: CO + Cl₂ ↔ COCl₂. Визначити вихідні концентрації хлору і оксиду карбону, якщо рівноважні концентрації фосгену, хлору і оксиду карбону відповідно дорівнюють 1; 0,1 і 0,05 моль/л. Відповідь: 1,1; 1,05 моль/л.

147. При деякій температурі і тиску в місткості ємністю 0,5 л знаходиться 0,03 моль діоксиду нітрогену. Визначити константу швидкості прямої реакції, що протікає за рівнянням 2NO₂ = N₂O₄, якщо швидкість реакції при даних умовах дорівнює 1,08 моль/л∙с. Відповідь: 300 л/моль∙с.

147. Обчислити константу рівноваги реакції 2HBr ↔ H₂ + Br₂, якщо вихідна маса гідрогенброміду дорівнювала 0,809 г, а до моменту рівноваги прореагувало 5% вихідної речовини. Відповідь: 0,9 ∙ 10^-4.

147. В ємність 0,5 л було вміщено 0,5 моль водню і 0,5 моль азоту. При деякій температурі до моменту рівноваги утворилось 0,02 моль аміаку. Обчислити константу рівноваги даної системи. Відповідь: 1,97 ∙ 10^-3.

147. В ємності місткістю 0,5 л протікає реакція СН_4(г) + Н₂О_(г) = СО_(г) + 3Н_2(г). Обчислити константу рівноваги даної реакції, якщо вихідні маси реагуючих речовин в даному об’ємі були такі: СН₄ – 0,8; Н₂О – 0,9; СО – 1,4; Н₂ – 0,12 г і якщо до моменту рівноваги прореагувало 50% метану. Відповідь: 0,937.

147. При деякій температурі склад рівноважної суміші в об’ємі 10 л був наступний: СО - 11,2; Cl₂ – 14,2; COCl₂ – 19,8 г. Обчислити константу рівноваги реакції CO + Cl₂ ↔ COCl₂ при даних умовах. Відповідь: 25.

147. Обчислити константу рівноваги реакції N₂ + 3H₂ ↔ 2NH₃, якщо при деякій температурі і тиску в ємність місткістю 10 л було введено 1,4 г азоту і 1 г водню. До моменту рівноваги утворилось 0,85 г аміаку. Відповідь: 6,9.

147. Реакція іде за рівнянням N₂ + O₂ = 2NO. Концентрації речовин до початку реакції були: азоту – 0,049; кисню – 0,010 моль/л. Обчислити концентрації цих речовин в момент, коли концентрація оксиду нітрогену складала 0,005 моль/л. Відповідь: 0,0465; 0,0075 моль/л.

147. Реакція протікає за рівнянням N₂ + 3H₂ ↔ 2NH₃. Концентрації речовин були такі: азоту – 0,8; водню – 1,5; аміаку – 0,1 моль/л. Обчислити концентрації водню і аміаку, коли концентрація азоту стала 0,5 моль/л. Відповідь: 0,6; 0,7 моль/л.

147. Реакція іде за рівнянням H₂ + I₂ = 2HI. Константа швидкості цієї реакції при 508^оС дорівнює 0,16. Вихідні концентрації реагуючих речовин: водню – 0,04; йоду – 0,05 моль/л. Обчислити початкову швидкість реакції і її швидкість, коли концентрація водню дорівнювала 0,03 моль/л. Відповідь: 3,2 ∙ 10^-4; 1,92 ∙ 10^-4 моль/л∙с.

147. Рівновага в гомогенній системі 4HCl + O₂ ↔ 2H₂O + 2Cl₂ встановилась при таких концентраціях реагуючих речовин; води – 0,14; хлору – 0,14; хлороводню – 0,2; кисню – 0,32 моль/л. Обчислити вихідні концентрації хлороводню і кисню. Відповідь: 0,48; 0,39 моль/л.

147. В газовій суміші з початковими концентраціями : СО – 0,01; Н₂О – 0,02; Н₂ – 0,01; СО₂ – 0,01 моль/л протікає хімічна реакція за рівнянням: СО + Н₂О = СО₂ + Н₂. Концентрація СО в стані рівноваги дорівнює 0,007 моль/л. Обчислити константу рівноваги цієї реакції. Відповідь: 1,42.

147. Вихідна суміш складається з 0,3 моль/л Н₂ і 0,2 моль/л N₂. Рівновага наступає, коли прореагує 0,24 моль/л Н₂. Обчислити константу рівноваги, якщо рівняння хімічної реакції N₂ + 3H₂ ↔ 2NH₃. Відповідь: 987,6.

147. Змішують 0,08 моль/л SO₂ і 0,06 моль/л О₂. Реакція 2SO₂ + О₂ ↔ 2SO₃ протікає в закритій ємності при постійній температурі. До моменту рівноваги в суміші залишається 20% вихідної кількості SO₂. Обчислити константу рівноваги цієї реакції. Відповідь: 570.

147. При синтезі аміаку при деяких умовах в рівновазі знаходяться 0,1 моль/л N₂, 0,2 моль/л Н₂ і 0,8 моль/л NH₃. Обчислити константу рівноваги і розрахувати вихідні концентрації азоту і водню. Відповідь: 800; 0,5; 1,4 моль/л.

147. При деякій температурі константа рівноваги гетерогенної реакції FeO_(т) + CO_(г) ↔ Fe_(т) + CO_2(г) дорівнює 0,5. Чому дорівнюють рівноважні концентрації СО і СО₂, якщо їх початкові концентрації дорівнюють, відповідно, 0,05 і 0,01 моль/л? Відповідь: 0,04; 0,02 моль/л.

147. Константа рівноваги гомогенної системи СО + Н₂О ↔ СО₂ + Н₂ при деякій температурі дорівнює 1. Обчислити рівноважні концентрації всіх реагуючих речовин, якщо вихідні концентрації СО і Н₂О відповідно дорівнюють 0,1 і 0,4 моль/л. Відповідь: 0,02; 0,32; 0,08; 0,08 моль/л.

147. Константа рівноваги гомогенної системи N₂ + 3H₂ ↔ 2NH₃ при температурі 400^оС дорівнює 0,1. Рівноважні концентрації водню і аміаку, відповідно, дорівнюють 0,2 і 0,08 моль/л. Обчислити рівноважну і вихідну концентрації азоту. Відповідь: 8; 8,04 моль/л.

147. Вихідні концентрації NO i Cl₂ в гомогенній системі 2NO + Cl₂ ↔ 2NOCl складають, відповідно, 0,5 і 0,2 моль/л. Обчислити константу рівноваги, якщо до моменту встановлення рівноваги прореагувало 20% NO. Відповідь: 0,416.

147. Визначити вихідні концентрації азоту і водню, якщо при рівновазі системи N₂ + 3H₂ ↔ 2NH₃ концентрації речовин були: N₂ – 0,5; H₂ – 0,3; NH₃ – 2 моль/л. Відповідь: 1,5 і 3,3 моль/л.

147. Визначити константу рівноваги реакції СО₂ + Н₂ ↔ СО + Н₂О, якщо при температурі 500^оС рівноважна суміш містить: СО₂ – 4%, Н₂ – 64%, Н₂О – 16%, СО – 16%.Обчислити (в %) вихідні концентрації СО і Н₂. Відповідь: 1; 20%; 80%.

147. При рівновазі в системі СО₂ + Н₂ ↔ СО + Н₂О концентрації речовин були СО₂ – 0,004; Н₂ – 0,001; СО – 0,02; Н₂О – 0,02 моль/л. Обчислити константу рівноваги і вихідні концентрації реагентів. Відповідь: 0,01; 0,024; 0,021 моль/л.

147. При рівновазі в системі 4HCl + O₂ ↔ 2Cl₂ + 2H₂O в об’ємі 0,5 л містилось (в г): HCl – 3,65; O₂ – 3,2; Cl₂ – 7,1; H₂O – 1,8. Обчислити константу рівноваги даної реакції. Відповідь: 5.

147. В результаті реакції 2Н₂ + О₂ = 2Н₂О через деякий час після її початку утворилось 5,4 г води. Які були при цьому концентрації водню і кисню, якщо вихідні кількості водню (20 г) і кисню (12,8 г) знаходились в ємності 100 л? Відповідь: 97 і 2,5 ммоль/л.

241. Обчислити середню константу швидкості реакції ІІ порядку утворення фосгену CO + Cl₂ = COCl₂ , якщо при 300 К кількість реагуючих речовин змінюється так:

Час, хв. 0 12 24

С – конц. СО,

моль/л. 0,01873 0,01794 0,01734.

Визначити концентрацію СО через 3 години після початку реакції.

Відповідь: 0,1871 л моль^-1хв^-1; 1,15 моль/л.

242. Константа швидкості реакції першого порядку дорівнює 5,2 ∙ 10^-2 хв^-1. Визначити скільки процентів вихідної речовини розкладеться за 10 хв і скільки часу потрібно для розкладу 99% вихідної речовини. Відповідь: 40,57%; 88 хв. 36 с.

₂₁₀

243. Активність ізотопу полонію ₈₄Ро за 35 діб зменшилася на 16,1%. Визначити константу швидкості розпаду, період напіврозпаду і час, протягом якого розпадається 90% вихідної кількості ізотопу полонію. Відповідь: 5,015 ∙ 10^-3діб^-1; 138,2 доби; 460,3 доби.

244. Речовину А змішано в рівних кількостях з речовинами В і С. Через 10 хв. половина речовини А прореагувала. Скільки залишиться речовини (в %) через 20 хв., якщо відповідна реакція першого порядку? Відповідь: 25%.

244. Константа швидкості гідролізу атропін-основи у водному розчині при 298 К дорівнює 6,01∙ 10^-7 хв^-1. Обчислити термін зберігання розчину (час розкладання 10% речовини) при даній температурі. Відповідь: 121,7 доби.

244. У реакції протолітичного розщеплення похідної ароматичних триазинів, що має протипухлинну дію, за 95 хв. прореагувала половина вихідної речовини. Скільки часу потрібно, щоб реакція в цих же умовах пройшла на 75%, якщо процес підпорядковується кінетичному рівнянню першого порядку% ? Відповідь: 190 хв.

244. Константа швидкості розкладу пеніциліну при 293 К дорівнює 3,12 ∙ 10^-7 хв^-1. Розрахуйте термін зберігання (час розкладу 10% лікарської речовини) препарату при даній температурі. Відповідь: 234,5 доби.

244. Розклад лікарської речовини при 333 К пройшов за 10 годин на 5%. Обчислити константу швидкості реакції. Відповідь: 8,55 ∙ 10^-5 хв^-1.

244. Константа швидкості інверсії сахарози в присутності іонів гідрогену становить 3,12 ∙ 10^-3 хв^-1. Через скільки хвилин прореагує 30% сахарози? Відповідь: 114,3.

244. При вивченні стійкості ніфедіпину, що застосовується в терапії серцево-судинних захворювань, було встановлено, що фотолітичний розпад препарату в рідкій лікарській формі підпорядковується кінетичному рівнянню першого порядку. Час напіврозпаду препарату при 50^оС становить 25,29 год. Розрахуйте кількість ніфедіпину (у відсотках), що розпався при 50^оС за 80 хв., а також час, протягом якого розпадається 10% препарату. Відповідь: 3,85%; 3,9 год.

244. Константа швидкості лужного гідролізу антибактеріального препарату діоксидину при 40^оС і однакових початкових концентраціях реагентів (С_о = 0,1 моль/л) становить 1,7 ∙ 10^-2 л моль^-1 с^-1. Розрахуйте період напівперетворення і кількість діоксидину, що прореагував за 2хв. Відповідь: 9,8 хв.; 0,017 моль/л.

244. Розчин лікарської речовини містить 300 активних одиниць в 1мл. Через 20 діб залишилось 100 одиниць в 1 мл. Розрахуйте період напівперетворення, якщо це реакція першого порядку. Відповідь: 12,63 доби.

244. Скільки часу потрібно для того, щоб реакція другого порядку пройшла на 60%, якщо за 20 хв вона проходить на 30%? Початкові концентрації вихідних речовин однакові і становлять 2 моль/л. Відповідь: 70 хв.

244. Було знайдено, що в деякій реакції при зміні початкової концентрації від 0,502 до 1,007 моль/л період напіврозпаду зменшується від 51 до 26 с. Визначити порядок і константу швидкості цієї реакції. Відповідь: другий; 0,0386 л моль^-1 с^-1.

244. Концентрація атомів тритію в повітрі приблизно 5 ∙ 10^-15 моль/л. Період напіврозпаду тритію – 12 років. Через скільки років розпадеться 90% тритію, який є в повітрі? Відповідь: 39,8 р.

244. Реакція першого порядку проходить за 10 хв. на 25%. Скільки треба часу, щоб реакція пройшла на 50% за тієї ж температури? Відповідь: 24 хв.

244. Константа швидкості реакції CH₃COOC₂H₅ + NaOH = CH₃COONa + C₂H₅OH дорівнює 5,4 хв^-1моль^-1л. Визначити кількість (в%) ефіру, яка прореагувала за 10 хв., якщо початкові концентрації лугу і ефіру 0,02 моль/л. Відповідь: 52%.

244. Розклад лікарського препарату при 298 К пройшов за 10 годин на 5%. Обчислити термін зберігання препарату (час розкладання 10% речовини) при даній температурі. Відповідь: 20,54 год.

244. Константа швидкості реакції першого порядку дорівнює 6,8 ∙ 10^-2 хв^-1. Визначити, скільки процентів вихідної речовини розкладеться за 20 хв і скільки часу потрібно для розкладу 95% вихідної речовини. Відповідь: 74,33%; 44 хв.

244. Розклад лікарського препарату при 300 К пройшов за 20 годин на 5%. Обчислити термін зберігання препарату (час розкладання 10% речовини) при даній температурі. Відповідь: 40,94 год.

244. Константа швидкості реакції першого порядку дорівнює 4,8 ∙ 10^-2 хв^-1. Визначити, скільки процентів вихідної речовини розкладеться за 25 хв. і скільки часу потрібно для розкладу 90% вихідної речовини. Відповідь: 69,9%; 48 хв.

244. Розклад лікарського препарату при 310 К пройшов за 24 години на 2%. Обчислити термін зберігання препарату (час розкладання 10% речовини) при даній температурі. Відповідь: 125,16 год.

244. Константа швидкості реакції першого порядку дорівнює 2,6 ∙ 10^-2 хв^-1. Визначити, скільки процентів вихідної речовини розкладеться за 15 хв.і скільки часу потрібно для розкладу 98% вихідної речовини. Відповідь: 32,3%; 150,5 хв.

244. Розклад лікарського препарату при 273 К пройшов за 12 годин на 1%. Обчислити термін зберігання препарату (час розкладання 10% речовини) при даній температурі. Відповідь: 125,8 год.

244. Тривалість реакції при температурі 300 К становить 630 хв. Скільки часу буде потрібно для проходження реакції при 320 К, якщо температурний коефіцієнт швидкості дорівнює 3? Відповідь: 70 хв.

244. Тривалість реакції при температурі 280 К становить 540 хв. Скільки часу буде потрібно для проходження реакції при 300 К, якщо температурний коефіцієнт швидкості дорівнює 3? Відповідь: 60 хв.

244. Тривалість реакції при температурі 380 К становить 450 хв. Скільки часу буде потрібно для проходження реакції при 400 К, якщо температурний коефіцієнт швидкості дорівнює 3? Відповідь: 50 хв.

244. Тривалість реакції при температурі 420 К становить 320 хв. Скільки часу буде потрібно для проходження реакції при 450 К, якщо температурний коефіцієнт швидкості дорівнює 2? Відповідь: 40 хв.

244. При якій температурі слід проводити реакцію, щоб швидкість її в порівнянні зі швидкістю при 323 К збільшилась в 10 разів? Температурний коефіцієнт швидкості реакції - 2,5. Відповідь: 348 К.

244. Період напіврозпаду речовини в реакції першого порядку при 323 К дорівнює 100 хв., а при 353 К – 15 хв. Визначити температурний коефіцієнт швидкості реакції. Відповідь: 1,88.

244. Протягом року при 30^оС розкладається 5% медичного препарату. Розрахувати константу швидкості процесу розкладу при 20^оС, якщо енергія активації становить 96,7 кДж/моль. Відповідь: 1,38 ∙ 10^-2 рік^-1.

244. Протягом року при 30^оС розкладається 10% медичного препарату. Розрахувати константу швидкості процесу розкладу при 20^оС, якщо енергія активації становить 81,7 кДж/моль. Відповідь: 3,45 ∙ 10^-2 рік^-1.

244. Йодоформ при зберіганні самодовільно розкладається з утворенням йоду. Протягом року при 40^оС розкладається 10% препарату. Розрахувати константу швидкості процесу розкладу при 25^оС, якщо енергія активації становить 91,2 кДж/моль. Відповідь: 1,79 ∙ 10^-2 рік^-1.

244. Початкова швидкість реакції розкладу аспірину у водному розчині при 20^оС становить 3,2 ∙ 10^-7 л^-1моль хв.^-1. Обчислити константу швидкості реакції при 40^оС, якщо вихідна концентрація аспірину у розчині становить 0,05 моль/л, а енергія активації дорівнює 126 кДж/моль. Відповідь: 2,02 ∙ 10^-4 хв.^-1.

244. Початкова швидкість реакції розкладу аспірину у водному розчині при 40^оС становить 2,2 ∙ 10^-7 л^-1моль хв.^-1. Обчислити константу швидкості реакції при 60^оС, якщо вихідна концентрація аспірину у розчині становить 0,04 моль/л, а енергія активації дорівнює 116 кДж/моль. Відповідь: 8,05 ∙ 10^-5 хв.^-1.

244. Початкова швидкість реакції розкладу амідопірину у водному розчині при 30^оС становить 6,2 ∙ 10^-7 л^-1моль хв.^-1. Обчислити константу швидкості реакції при 60^оС, якщо вихідна концентрація амідопірину у розчині становить 0,02 моль/л, а енергія активації дорівнює 136 кДж/моль. Відповідь: 4,25 ∙ 10^-3 хв.^-1.

244. Початкова швидкість реакції розкладу амідопірину у водному розчині при 20^оС становить 3,2 ∙ 10^-7 л^-1моль хв.^-1. Обчислити константу швидкості реакції при 50^оС, якщо вихідна концентрація амідопірину у розчині становить 0,04 моль/л, а енергія активації дорівнює 142 кДж/моль. Відповідь: 1,81 ∙ 10^-3 хв.^-1.

244. Початкова швидкість реакції розкладу амідопірину у водному розчині при 25^оС становить 4,1 ∙ 10^-7 л^-1моль хв.^-1. Обчислити константу швидкості реакції при 50^оС, якщо вихідна концентрація амідопірину у розчині становить 0,05 моль/л, а енергія активації дорівнює 112 кДж/моль. Відповідь: 1,81 ∙ 10^-3 хв.^-1.

244. Константа швидкості для реакції Н₂ + І₂ ↔ 2НІ при 563 К дорівнює 4,59 ∙ 10^-2, а при 767 К – 0,248 моль^-1л хв.^-1. Константи швидкості зворотної реакції при цих температурах відповідно дорівнюють 4,67 ∙ 10^-4 і 2,38 ∙10^-2 моль^-1л хв.^-1. Визначити константи рівноваг для цих температур. Відповідь: 98,29; 10,42.

244. Константа швидкості для реакції Н₂ + І₂ ↔ 2НІ при 683 К дорівнює 6,59 ∙ 10^-2, а при 716 К – 0,375 моль^-1л хв.^-1. Константи швидкості зворотної реакції при цих температурах відповідно дорівнюють 5,12 ∙ 10^-4 і 2,50 ∙10^-2 моль^-1л хв.^-1. Визначити константи рівноваг для цих температур. Відповідь: 128,7; 15,0.

244. Константи швидкості омилення етилацетату лугом при 282,6 і 287,6 К відповідно дорівнюють 2,37 і 3,204 моль^-1л хв.^-1. При якій температурі константа швидкості цієї реакції дорівнюватиме 4 моль^-1л хв.^-1? Відповідь: 291,3 К.

244. Визначити енергію активації реакції H₂ + Br₂ = 2HBr, якщо при 550,7 і 574,5 К константи швидкості реакції відповідно дорівнюють 1,59 ∙10^-2 і 8,56 ∙10^-2 моль^-1л хв.^-1. Відповідь: 186,1 кДж.

244. У скільки разів збільшується швидкість реакції розкладу діоксиду нітрогену при підвищенні температури від 610 до 630 К, якщо в цьому інтервалі температур енергія активації реакції дорівнює 123 кДж? Відповідь: в 2,16 раз.

244. У скільки разів збільшується швидкість реакції розкладу діоксиду нітрогену при підвищенні температури від 600 до 640 К, якщо в цьому інтервалі температур енергія активації реакції дорівнює 113 кДж? Відповідь: в 4,14 раз.

244. Константа швидкості розкладу пероксиду гідрогену йодистоводневою кислотою при температурах 313 і 323 К відповідно дорівнює 3,24 і 6,62 моль^-1л хв.^-1. Визначити енергію активації і константу швидкості реакції при 318 К. Відповідь: 59,89 кДж; 4,63 моль^-1л хв.^-1.

244. Константа швидкості розкладу пероксиду гідрогену йодистоводневою кислотою при температурах 303 і 313 К відповідно дорівнює 4,64 і 8,63 моль^-1л хв.^-1. Визначити енергію активації і константу швидкості реакції при 308 К. Відповідь: 48,79 кДж; 6,33 моль^-1л хв.^-1.

244. Константа швидкості розкладу пероксиду гідрогену йодистоводневою кислотою при температурах 293 і 303 К відповідно дорівнює 4,32 і 8,38 моль^-1л хв.^-1. Визначити енергію активації і константу швидкості реакції при 298 К. Відповідь: 48,77 кДж; 6,02 моль^-1л хв.^-1.

244. Період напіврозпаду речовини в реакції першого порядку при 273 К дорівнює 80 хв., а при 303 К – 10 хв. Визначити температурний коефіцієнт швидкості цієї реакції. Відповідь: 2.