Лекции по вычмату преподавателя Друка / L015

Лекция 15. МЕТОДЫ ПЕРВОГО ПОРЯДКА.

15.1. Метод градиента.

Введем обозначение для , т.е. для градиента функции. Напомним, что - это вектор, компоненты которого равны значениям частных производных по соответствующим координатам, т.е.

(15.1)

Вектор может вычисляться в любой точке и дает направление наискорейшего возрастания функции в этой точке. Пусть - это шаг (step в английском языке) из рассматриваемой точки в новую точку и

,

(15.2)

где , , - это векторы, т.е. массивы длины . Сложение в (15.2) выполняется для векторов (см. рис. 15.1).

Рис. 15.1. Шаг из точки в новую точку в многомерном пространстве.

Метод градиента заключается в том, что точка определяется в результате одномерного поиска минимума в направлении антиградиента для точки . Шаги прекращаются при попадании в - окрестность точки минимума и при малых значениях , т.к. в точке минимума .

АЛГОРИТМ

Дана функция , формулы или алгоритм для вычисления градиента по (15.1), выбрана начальная точка и значение допустимой погрешности . Начальная точка может выбираться либо произвольной, либо на основании дополнительной информации о расположении минимума.

1. Вычислить компоненты . Обычно для этого применяют численное дифференцирование функции по каждой координате.

2. Выполнить одномерный поиск вдоль направления (). В результате получается следующая точка .

3. Проверить условия , .

Если условия выполняются, то - это точка минимума. Иначе и на пункт 1.

В этом алгоритме не учтена защита от зацикливания, которая должна быть обязательно. Например, можно указать некоторое максимальное количество шагов в операторе цикла, или предусмотреть вывод каких-то сообщений после некоторого большого количества шагов. Отметим, что малые значения могут соответствовать не точке минимума, а седловой точке.

На рис. 15.2. приведен пример поиска минимума методами координатного и наискорейшего спуска.

Рис. 15.1. Шаг из точки в новую точку в многомерном пространстве.

Метод градиента работает быстрее, чем прямые методы, т.к. использует информацию о производных. Но у него есть два существенных недостатка: трудности вычисления производных для сложных функций и большое количество шагов для так называемых овражных целевых функций, к рассмотрению которых и переходим.

Так как в любой точке при поиске минимума многомерных функций множество приемлемых направлений бесконечно, то именно способ выбора направления определяет суть алгоритма, а к вычислению величины шага принято относиться как к некой отдельной процедуре, результаты которой менее важны.

15.2. Овражные целевые функции.

Рассмотрим случай двух переменных и целевую функцию, у которой линии уровня представляют собой сильно вытянутые эллипсы, см. рис. 15.3. Минимум обозначен точкой и находится примерно в центре линий. В общем случае эти эллипсы нужно представить в многомерном пространстве, они узки, сильно деформированы и линии уровня имеют извилистый характер.

Функции, у которых линии уровня образуют сильно вытянутые замкнутые кривые, называют овражными, т.к. такие линии уровня соответствуют реальным оврагам.

Рис.15.3. Поиск минимума для овражных функций.

Отметим, что хорошими специалистами по построению линий уровня являются ослы, т.к. они чувствительны к степени отклонения их пути от горизонтали. В гористой местности с помощью ослов выбирают трассы каналов.

Вернемся к рис.15.3. Стрелки на линиях дают направление антиградиентов для некоторых точек. Видим, что только для точек A, B, C, D эти стрелки дают правильное направление для поиска минимума, а для других точек одномерный поиск будет выводить на дно оврага, причем приближение к минимуму будет очень медленным. Траектория поиска будет зигзагообразной и это показано на рисунке. Ее можно представить себе как перекатывание шарика с одного склона на другой при общей тенденции спуска в точку минимума . Это же движение можно представить как поиск в полной темноте источника воды на дне очень узкого, длинного оврага путем пробных шагов. Такие зигзагообразные траектории резко увеличивают количество шагов при поиске минимума.

Появление оврагов в целевых функциях можно объяснить взаимным влиянием входных параметров, плохим выбором их масштабов изменения, различием в чувствительности функции к изменению параметров. Обычно на дне оврага все параметры примерно одинаково влияют на целевую функцию, а на склонах существенно влияние лишь нескольких из рассматриваемых.

Строгая проверка наличия оврагов очень сложна и требует вычисления собственных значений матрицы Гессе (14.5), которые изменяются при движении точки поиска вместе с изменением матрицы Гессе. Овражному характеру соответствует существенное различие модулей собственных значений.

Как правило, в практических задачах овраги есть, но т.к. исследовать их наличие очень сложно, то предпочитают не заниматься этим, а использовать методы поиска, которые сохраняют свою эффективность для овражных функций.

В заключение этого раздела рассмотрим кратко вопрос о масштабировании для целевых функций. Масштабирование обычно выполняется заменой переменных и при этом от переменных, отражающих физическую сущность задачи, переходят к новым, более подходящим для метода ее решения.

В некоторых задачах простое изменение диапазона входных параметров может устранить овражный характер целевых функций. Для этого рекомендуется нормировать входные параметры так, чтобы область поиска для каждой переменной находилась в диапазоне от -1 до 1. Например, если - это оценка для области изменения переменной , то замена

,

(15.3)

дает . Отметим, что эта рекомендация по нормированию переменных полезна и для регрессионных моделей раздела 2.2.

Значения целевой функции полезно масштабировать для уменьшения влияния погрешностей. Плохо, если значения F всюду близки к нулю или содержат большую постоянную составляющую. Желательно, чтобы в окрестности искомой точки модули значений целевой функции были величинами порядка единиц или меньше. Это связано с тем, что в реальных алгоритмах используются как относительные погрешности, так и абсолютные.

15.3. Метод сопряженных градиентов.

Этот метод можно рассматривать как усовершенствование метода градиента для более эффективного поиска минимума овражных функций. Отметим, что в разделе 14.4 переход от метода покоординатного спуска к методу Розенброка также обеспечивал поиск минимума для овражных функций.

Название метода основано на математическом понятии сопряженности двух векторов , относительно матрицы :

,

Можно показать, что для многомерной квадратичной функции во многих случаях наилучшим направлением поиска является направление, сопряженное с предыдущим направлением поиска.

В методе градиента на текущем шаге все вычисления повторялись независимо от предыдущих шагов, т.е. значение градиента в точке не использовалось при вычислении нового шага из точки в следующую. В методе сопряженных градиентов при определении текущего шага из точки учитываются два градиента - в точке этого шага и в точке предшествующего шага, см. рис.15.4. Движение из начальной точки начинается по обычному методу градиента.

Рис.15.4. Вычисление текущего шага в методе сопряженных градиентов.

Алгоритм метода.

1. Выбор начальной точки , вычисление антиградиента в этой точке, одномерный поиск минимума целевой функции в этом направлении , получаем соответствующий этому минимуму точку .

2. Вычисление антиградиента функции в точке .

3. Определение нового направления движения учитывающего градиенты в точках , по формуле

,

(15.4)

где коэффициент рассчитывается из условия - сопряженности векторов и .

,

(15.5)

где

,

(15.6)

- матрица Гессе, являющаяся аналогом 2-й производной в многомерном пространстве . Подставляя (15.4) в (15.5), получаем

, откуда

.

(15.7)

Определение по этой формуле требует значительного объема вычислений, поэтому часто используют упрощенное выражение

,

(15.8)

4. Одномерный поиск минимума целевой функции в направлении , приводящий в точку .

5. Проверим условия нахождение минимума . Если условие выполняется, то - точка минимума , определенная с погрешностью . Иначе итерации надо продолжать, переходя из в и т.д. по тому же алгоритму, пока не получим на -й итерации .

Для определения минимума в этом методе требуется примерно шагов, где - количество аргументов в целевой функции. Это значительно меньше, чем в методе Розенброка, но сами шаги (итерации) существенно сложнее. Заметим, что использование на текущем шаге результатов вычислений с предшествующего шага аналогично учету предшествующих шагов в многошаговых методах решения ОДУ.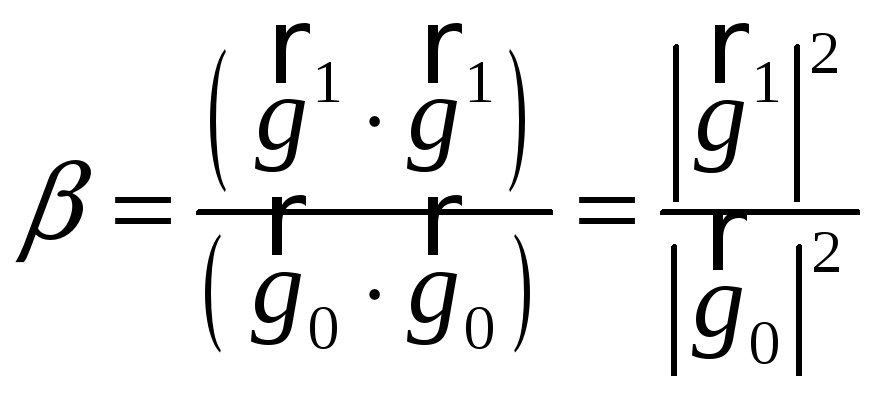