- •1.1. Математические модели.
- •1.2. Аналитические и алгоритмические математические модели.
- •1.3. Непрерывные и дискретные функции.
- •1.4. Интерполяция и аппроксимация функций.
- •1.5. Интерполяция полиномами.
- •1.5.1. Интерполяция с помощью решения слау (системы линейных алгебраических уравнений).
- •1.5.2. Интерполяция методом Лагранжа.
- •1.5.3. Интерполяция методом Ньютона.
|
Лекция 1. Математические модели и интерполяция. |
1.1. Математические модели.
Модель - это упрощенное подобие объекта. Физические эксперименты, которые Вы проводили в лабораториях по физике, имеют дело с физическими объектами или с их моделями, учитывающими основные свойства моделируемых объектов. Эксперименты с физическими объектами, исследуемыми с помощью конкретной измерительной и другой аппаратуры, обычно называют натурными. Все эти исследования можно провести с помощью компьютера, если в качестве исследуемого объекта выбрать его математическую модель.
Математическая модель (ММ) - это совокупность математических объектов (чисел, констант, переменных, векторов, матриц, множеств) и отношений между ними (функций, формул, уравнений, систем уравнений, операторов), которая адекватно, т.е. правильно, отображает все те свойства физического объекта, которые интересуют инженера или исследователя. В латыни слово ad-aequatus означает «почти равный».
Модель считается адекватной, если она проверена, т.е. хорошо протестирована, и позволяет предсказывать поведение объекта в различных условиях с требуемой точностью. Все математические модели адекватны лишь в определенной области изменения параметров объекта. Отметим, что для таких общих математических моделей, как уравнения Максвелла или уравнения гравитации Эйнштейна, область адекватности очень велика, тогда как для простых моделей она обычно очень ограничена.
На
рис.1.1 условно показан натурный эксперимент
с физическим объектом и его математическое
моделирование. Векторы
![]() ,
,![]() ,
,![]() соответствуют физическим характеристикам,
векторы
соответствуют физическим характеристикам,
векторы![]() ,
,![]() - это аналогичные характеристика в ММ:
- это аналогичные характеристика в ММ:![]() - внешние воздействия,
- внешние воздействия,![]() - параметры объекта,
- параметры объекта,![]() - выходные характеристики, вектор
- выходные характеристики, вектор![]() в ММ является вектором входных параметров,
т.е.
в ММ является вектором входных параметров,
т.е.![]() ,
и он объединяет входные воздействия и
параметры объекта.
,
и он объединяет входные воздействия и
параметры объекта.
|
натурный эксперимент |
математическое моделирование |
|
Рис.1.1. | |
Количество
входных параметров, учитываемых в ММ,
может быть различным. Обычно чем больше
параметров в модели, тем меньше погрешность
результатов, получаемых с помощью этой
ММ. На рис.1.2 приведена качественная
зависимость погрешности моделирования
![]() от количества учитываемых в ММ параметров
от количества учитываемых в ММ параметров![]() для некоторого обобщенного объекта
моделирования, причем
для некоторого обобщенного объекта
моделирования, причем![]() соответствует 100%.
соответствует 100%.
|
|
|
Рис.1.2. Зависимость погрешности моделирования от количества параметров в ММ. |
1.2. Аналитические и алгоритмические математические модели.
Показанная на рис. 1.1 математическая модель (ММ) может быть представлена:
- формулой,
- несколькими формулами,
- различными уравнениями,
- программой, реализующей совокупность некоторых алгоритмов.
ММ
является аналитической,
если зависимость выходного параметра
![]() от входного
от входного![]() можно записать в явном виде, т.е. в виде
функции
можно записать в явном виде, т.е. в виде
функции![]() или
или![]() ,
где вектор
,
где вектор
![]() соответствует случаю многих переменных.
Если модель в виде одной или нескольких
функций записать нельзя, тоММ
называется алгоритмической.
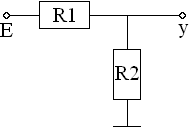
В качестве примера рассмотрим
математические модели для трех физических
объектов: двух схем и диода (см. рис.1.3).
соответствует случаю многих переменных.
Если модель в виде одной или нескольких
функций записать нельзя, тоММ
называется алгоритмической.
В качестве примера рассмотрим
математические модели для трех физических
объектов: двух схем и диода (см. рис.1.3).
|
Физический объект |
|
|
|
|
Входные параметры |
|
|
|
|
ММ |
|
|
|
|
Тип модели |
Аналитическая |
Аналитическая |
Алгоритмическая |
|
Рис.1.3. | |||
В
последнем случае модель является
алгоритмической, т.к. решение полученного
нелинейного уравнения в виде формулы
![]() невозможно и нужно применять специальные
методы или стандартные программы. Обычно
для расчета сложных схем в радиоэлектронике
применяют алгоритмические ММ.
невозможно и нужно применять специальные
методы или стандартные программы. Обычно
для расчета сложных схем в радиоэлектронике
применяют алгоритмические ММ.