Шпоры по вычмату / 006

РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ.

Система линейных алгебраических уравнений (СЛАУ) имеет вид:

(3.1)

или в матричной форме Ax = B

- это матрица порядка , т.е. размера ,  - вектор неизвестных, т.е. одномерный массив длины ;  - вектор правых частей той же длины.

Методы решения СЛАУ обычно основаны на приведении матрицы в системе (3.2) к треугольному виду, т.к. системы с треугольными матрицами легко решаются путем последовательного нахождения одного неизвестного в каждом уравнении. Возможны нижняя или верхняя треугольные формы для матрицы, показанные на рис.3.1.

Рис. 3.1. Нижняя и верхняя треугольные матрицы в СЛАУ.

В нижней треугольной матрице все ненулевые элементы должны располагаться в нижнем треугольнике, а в матрице - в верхнем, причем главная диагональ может содержать ненулевые элементы. Для системы или первым решается уравнение или соответственно.

Метод Гаусса.

Для матриц общего вида любого порядка лучшим методом решения является метод Гаусса. Приведение к треугольному виду в нем (прямой ход) можно рассматривать как последовательное умножение обеих частей системы (3.2) на матрицы простой структуры, каждая из которых обращает в нуль один элемент .

На языке детективов - это "матрицы-убийцы". В результате получаем систему с треугольной матрицей , которая имеет новый вектор правых частей .

Рассмотрим подробнее порядок вычислений. Пусть в системе (3.1) (в противном случае надо переставить уравнения). Множим 1-е уравнение на и складываем с ным уравнением. Перебирая , уничтожаем 1-й член во всех этих уравнениях.

Получаем систему:

,

где , , . Это 1-й шаг.

На втором шаге множим уравнение (2) на и складываем с -ым уравнением. Перебирая , уничтожаем 1-й член во всех этих уравнениях

,

где , , .

На (-м) шаге имеем:

, , .

На шаге получаем систему с треугольной матрицей:

,

отсюда находим - это прямой ход. Далее обратным ходом восстанавливаем .

Количество операций в методе Гаусса пропорционально . Это количество операций можно резко сократить только для матриц специальной структуры, например, симметричных или содержащих большое количество нулей. Для каждой структуры обычно разрабатывается специальный метод, более эффективный, чем метод Гаусса. В случае определения коэффициентов кубического сплайна получается система с трехдиагональной матрицей, в которой все ненулевые элементы расположены на главной и соседних диагоналях. Системы с такими матрицами решаются методом прогонки, который можно рассматривать как частный случай метода Гаусса.  

Разреженные матрицы.

Эти матрицы состоят, в основном, из нулей и ненулевые элементы расположены нерегулярно, т.е. название матриц указывает на редкое расположение ненулевых элементов. Образ разреженной матрицы можно представить как квадрат на звездном небе, в котором звезды соответствуют ненулевым элементам.

Эти матрицы характеризуются степенью разреженности (обычно в %), 

,

где количество элементов равно для матрицы порядка .

При моделировании схем получаются разреженные матрицы. Например, для схемы с 10 узлами степень разреженности примерно 50%, для схемы со 100 узлами степень разреженности близка к 95% и при увеличении количества узлов значение стремится к 100%.

Применение стандартных подпрограмм в случае решения СЛАУ с разреженными матрицами методом Гаусса нецелесообразно по следующим причинам:

1.  При хранении матрицы память будет заполнена нулями.

2.  При выполнении операций с элементами будет много операций с нулями.

3.  После приведения к треугольному виду в ненулевом треугольнике будет мало нулей, т.е. разреженность этой части будет утрачена.

4. Приведение к треугольному виду требует также преобразования вектора .

Первый недостаток можно устранить, используя различные структуры для хранения ненулевых элементов, например, хранить для каждого такого элемента значения , , .

Эти структуры, а также устранение операций с нулями требуют существенного изменения стандартных программ для метода Гаусса. Третий и четвертый недостатки отсутствуют при решении СЛАУ методом LU-разложения.

LU-разложение.

При решении СЛАУ представим матрицу в виде произведения нижней и верхней треугольных матриц .

Для простоты рассмотрим сначала небольшой порядок матриц , причем все диагональные элементы матрицы положим равными единице. В этом случае получаем равенство:

.

Необычная нумерация элементов матриц позволяет проще сформулировать правила LU-разложения. Матрица задана, её коэффициенты известны.

Неизвестные элементы матриц и обозначены как и соответственно и поэлементное приравнивание обеих частей после перемножения матриц и даёт их значения. При этом важен порядок приравнивания. Его нужно вести "елочкой", т.е. сначала приравнивать все элементы первого столбца (, , в примере), затем первой строки (, ), далее идут столбец 2 (, ), строка 2 (), столбец 3 () и т.д. При таком порядке каждое равенство будет давать один неизвестный коэффициент, т.е. в результате всех приравниваний получим все коэффициенты. В данной матрице из первых трех равенств получим элементы , , из двух следующих , и т. д.

Запишем эти соотношения подробнее:

,

,

,

, ,

, ,

, ,

, ,

, ,

, .

После получения LU-разложения решается система , которая записывается в виде двух систем , . Эти две системы с треугольными матрицами решаются последовательно и результатом является вектор .

Для LU-разложения при произвольном размере матрицы можно использовать разные алгоритмы. Рассмотрим алгоритм Краута, возвращаясь к обычным обозначениям элементов матриц , , . Согласно исходному соотношению имеем после перемножения матриц

,

где верхний предел суммы учитывает наличие нулевых элементов в матрицах и .

Рассмотрим произвольный элемент на или под главной диагональю матрицы , для которого и заменим индекс на . При этом, положив , получим

или

,

(3.3)

Аналогичным образом, рассматривая произвольный элемент над главной диагональю, для которого , и использую индекс вместо , находим

.

После преобразования придем к следующему выражению для элементов матрицы :

,

(3.4)

Уравнения (3.3), (3.4) описывают алгоритм разложения на треугольные матрицы , при задании . Заметим, что требуемые в этих соотношениях значения элементов матриц и рассчитываются на предыдущих этапах процесса, что было проиллюстрировано выше на примере .

Обобщив все сказанное, опишем алгоритм LU-разложения следующим образом:

Шаг 1.	Положим и перейдем к шагу 3.
Шаг 2.	Используя (3.3), рассчитаем -й столбец матрицы . При закончим процедуру разложения.
Шаг 3.	Используя (3.4) рассчитываем -ю строку матрицы .
Шаг 4.	Положим и перейдем к шагу 2.

Основное достоинство метода LU-разложения - сохранение разреженной структуры матриц и , что при исключении операций с нулями позволяет уменьшить количество операций по сравнению с методом Гаусса. Если матрица не является разреженной, то количество операций в обоих методах примерно одинаково.

LU-рАЗЛОЖЕНИЕ.

Задача. Решить СЛАУ , проведением LU-разложение матрицы .

, .

При решении СЛАУ представим матрицу в виде произведения нижней и верхней треугольных матриц .

Матрица задана, её коэффициенты известны. Неизвестные элементы матриц и обозначены как и соответственно и поэлементное приравнивание обеих частей после перемножения матриц и даёт их значения. При этом важен порядок приравнивания. Его нужно вести "елочкой", т.е. сначала приравнивать все элементы первого столбца (, , ), затем первой строки (, ), далее идут столбец 2 (, ), строка 2 (), столбец 3 (). При таком порядке каждое равенство будет давать один неизвестный коэффициент, т.е. в результате всех приравниваний получим все коэффициенты. В данной матрице из первых трех равенств получим элементы , , из двух следующих , и т.д. Запишем эти соотношения подробнее:

, ;

, ;

, ;

, , ;

, , ;

, , ;

, , ;

, , ;

, , .

Получаем:

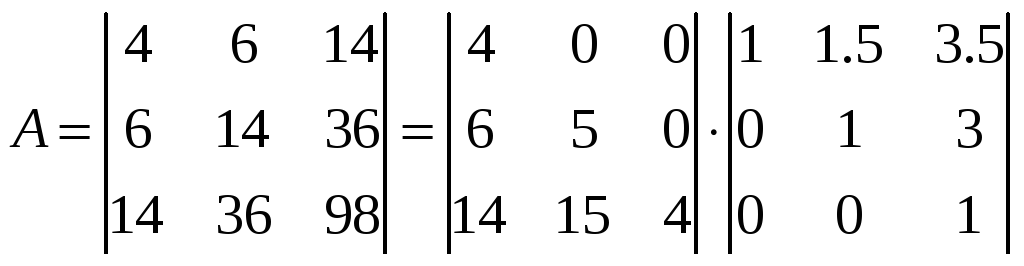, т.е. , .

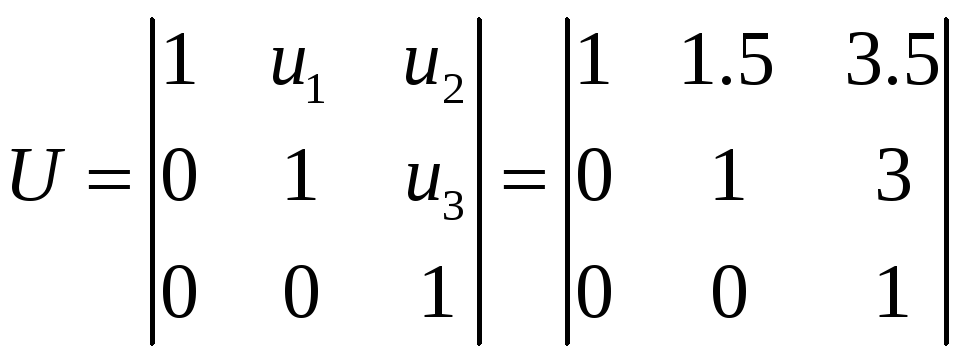После получения LU-разложения решается система , которая записывается в виде двух систем , . Эти две системы с треугольными матрицами решаются последовательно и результатом является вектор .

, , .

, , .

LU-разложения при произвольном размере матрицы.

Для LU-разложения при произвольном размере матрицы рассмотрим алгоритм Краута. Возвращаясь к обычным обозначениям элементов матриц , , .

Согласно исходному соотношению имеем после перемножения матриц

,

где верхний предел суммы учитывает наличие нулевых элементов в матрицах и .

Рассмотрим произвольный элемент на или под главной диагональю матрицы , для которого и заменим индекс на . При этом, положив , получим

или , (4.1)

или

Аналогичным образом, рассматривая произвольный элемент над главной диагональю, для которого , и использую индекс вместо , находим

.После преобразования придем к выражению для элементов матрицы :

,

(4.2)

Уравнения (4.1), (4.2) описывают алгоритм разложения на треугольные матрицы , при задании . Заметим, что требуемые в этих соотношениях значения элементов матриц и рассчитываются на предыдущих этапах процесса, что было проиллюстрировано выше на примере .

Задача. Решить СЛАУ , используя алгоритм Краута для проведения LU-разложение матрицы .