Шпоры по вычмату / 010

5.3. Метод Ньютона для одного уравнения.

Пусть функция задана в виде формулы и возможно ее дифференцирование для получения первой производной в виде формулы. Рассмотрим два первых слагаемых ряда Тейлора для вблизи начальной точки , что соответствует линейной интерполяции, и приравняем к нулю значение в новой точке :

(5.2)

Отсюда сразу получаем значение поправки

(5.3)

и новое значение

(5.4)

На -м шаге , .

Итерационный метод вычисления корня с применением формул (5.3 - 5.4) называется методом Ньютона или методом касательных, т.к. основан на вычислении производной. В зарубежной литературе его называют методом Ньютона-Рафсона.

На рис.5.2 показана геометрическая интерпретация метода Ньютона: касательная в начальной точке пересекает ось новой точке , в которой опять строится касательная и т.д.

Рис.5.2. Начало итераций в методе Ньютона: - начальная точка, - следующая.

Метод Ньютона - это самый эффективный метод по количеству итераций: решение получается примерно после двух-пяти итераций.

Недостатками его являются сложность вычисления производной, возможность (или не возможность) аналитического получения нулевых или малых значений в (5.3) на итерациях, возможность зацикливания в ряде случаев, показанная на рис.5.3., возможность переполнения в ЭВМ.

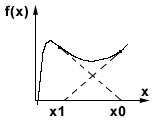
Пусть, например . Тогда при , получаем и .

Рис. 5.3. Иллюстрация возможности зацикливания в методе Ньютона при начальном значении .

Дана система двух уравнений для двух переменных , .

Расписать алгоритм нахождения корня уравнения с помощью метода Ньютона, сделать 3 итерации для нахождения корня.

1. Область определения корня вытекает из того, что ; , .

В этой области , ,

Система уравнений

- начальное значение корня;

- после 1-й итерации

Уравнение для :

; Якоби ;

Уравнения

Можно взять, , т.е. , , или , или другие комбинации , , .

Приближенный корень. Положим, что , .

, , .

Более точно , ()

,

,

, ,

, .