Теорема Кэли (1897)(частный случай матричной теоремы Кирхгофа, когда граф
является полным):
Число основных помеченных деревьев порядка V равноVV-2 .
Замечания:
Теорему Кэли легко доказать с помощью символа дерева (Т) и с помощью теоремы Трента; множество символов М={I(T)} длины V-2 можно рассматривать как множество картежей из элементов- номеров вершин, т.е.
М=VV…V=VV-2,
так и с привлечением теоремы Трента и
Кэли.
V-2 раз
Пример:
Для графа К5(полный граф с пятью вершинами) число покрывающих деревьев равно
М= 55-2 =125
Существенно различные (неизоморфные) покрывающие деревья подсчитывают комбинаторными методами с помощью генератрис (производящих функций)
Число неизоморфных корневых покрывающих деревьев Tn c V=n вершинами определяется не перечисляющимся рядом:
T(x)= Tnxn
n=1
Этот ряд удовлетворяет функциональному уравнению:
T(x)= x exp (1/r )T(x2)
r=1
Число неизолированных покрывающих деревьев (необязательно корневых) tn определяется перечисляющимся рядом
n
t(x)= tixi
i=1
Можно представить и в виде перечисляющегося ряда для корневых деревьев:
t(x)= T(x)- 0,5*[T2(x)- T(x2)].
Очевидно, что функциональные уравнения для Т(х) и t(x) позволяют вычислять Tn и tn для конкретных значений n
Пример:
Для полного графа К4 число покрывающих деревьев равно 44-2=16
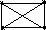
Представим их
Среди этих деревьев есть только 2 типа неизоморфных деревьев, т.е.
Теоремы и критерии о планарности графа.
Всякий подграф планарного графа планарен.
Граф планарен тогда и только тогда когда, когда каждая его связная компонента планарный граф.
Теорема Эйлера: «Для каждого связного и планарного графа справедлива формула Эйлера:
V-U+ Г=2».
Теорема Фари: «Для любого планарного графа существует плоское представление, в котором все ребра - прямолинейные отрезки».
Теорема о «раскраске» графа: «Для всякого планарного графа его хроматическое число () 5(возможно и () 4- это так называемая проблема о четырех красках, но то, что планарный граф является 4-х - хроматическим является предположение, не доказанное строго математически).
Критерий планарности графа Понтрягина – Куратовского: «Граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных К5 или К3,3»
Теоремы об изоморфизме графов.
Теорема Кенига: «Граф является двудольным тогда и только тогда, когда он не имеет циклов нечетной степени» (т.е. карта допускает раскраску в два цвета тогда и только тогда, когда каждая вершина имеет четную степень) или «Граф может быть представлен в виде двудольного графа, если все его циклы имеют четкое число ребер».
Два графа являются изоморфными, если они имеют одни и те же матрицы инцидентностей с точностью до перестановок строк и столбцов.
Теоремы о потоках в транспортной сети.
Теорема о максимальном истоке и минимальном разрезе: Величина каждого стационарного потока (U) для заданной транспортной сети из q(истока) в S(сток) не превышает пропускной способности минимального разреза, разделяющего q и S, причем существует поток, достигающий этого значения (эта теорема доказана Фордом и Фалкерсоном)
Теорема о целочисленности потока в транспортной сети: Если пропускная способность c(U) дуг Vi транспортной сети целочислена, то существует максимальный стационарный исток S max, который целочисленен.
Примечание:
Теорема о максимальном потоке и минимальном разрезе позволяет получить как следствия следующие теоремы:
Теорему о максимальном паросочетании в двудольном графе <V’, V”, U>:
Теорему о различных представлениях
Теорему о к - связности графов
Теорему о покрытии частично упорядоченного множества наименьшим числом цепей.